1. Introducción

La teoría tradicional de finanzas y desarrollo postula una relación directa entre el sector financiero y el desarrollo económico. Esta teoría ha sido extendida recientemente para sugerir una relación directa entre el desempeño de los mercados accionarios y el crecimiento económico. La evidencia empírica ha producido resultados que demuestran la presencia de un impacto bidireccional entre ambos sectores.

La gran volatilidad existente en el comportamiento de los mercados financieros internacionales durante las últimas décadas ha sido principalmente reflejo de la crisis económica mundial. Tornándose en la variable mayormente considerada por los inversionistas para tomar sus decisiones y provocando un cambio en la composición de los ingresos a escala global: se ha favorecido las inversiones en los mercados de capital sobre la inversión directa.

En la historia moderna de los mercados financieros se pueden resaltar hechos relevantes que han denotado la vulnerabilidad que se origina de eventos económicos: la crisis bursátil de Estados Unidos en 1987, los mercados emergentes del Sudeste asiático a mediados de 1997; en América Latina, la crisis se presentó en el segundo semestre de este año, poco después llegaron la crisis de Rusia, Brasil y Argentina. Los flujos de capitales durante este periodo estuvieron en conexión con el ciclo de negocios, por lo tanto, se redujo dramáticamente la participación de los inversionistas, aumentando con esto la presión en los mercados internacionales de capitales.

El proceso de declive en los ciclos económicos no solo se presentó en las economías emergentes, el dinamismo en la actividad económica de los países desarrollados también mostró la misma tendencia. Los mercados financieros internacionales, tanto emergentes como desarrollados, exhiben una mayor fragilidad en relación con el desempeño que muestra la economía más poderosa del mundo, la de Estados Unidos, que históricamente ha ostentado el papel de mayor inversionista del mundo. En vista de ello, mucho se ha dicho en estudios realizados por diversas instituciones financieras internacionales sobre el papel positivo o negativo que ejerce el desempeño económico de Estados Unidos sobre los mercados financieros internacionales. Si la economía de Estados Unidos se expande, fomenta la exportación y la actividad económica, pero tan pronto como la actividad se deprime la Reserva Federal de Estados Unidos contrae los flujos de capitales y los escenarios mundiales se complican, por ende, se afecta en mayor grado a aquellos países cuyas relaciones comerciales son más estrechas como es el caso de México y Canadá.

Recientemente, tras la apertura de los mercados internacionales a partir de la década de los noventas, la práctica de ignorar al resto del mundo es inadecuada (Chen, Roll y Ross, 1986); por lo cual es necesario incorporar en los estudios sobre mercados financieros la influencia de los mercados externos sobre la economía interna. Cuando se abren las economías al resto del mundo, existe una gran variedad de activos intercambiándose diariamente. Los inversionistas tienen que decidir cómo distribuir su riqueza financiera entre distintos tipos de activos financieros ofertados en diversos mercados y, por tanto, se deben introducir variables extranjeras influyendo en los factores nacionales.

Análogamente, la controversia académica sobre el vínculo entre el desarrollo financiero y el crecimiento económico ha estado presente desde los inicios del sistema financiero. Esta relación ha sido ampliamente estudiada por gran cantidad de autores. Entre las diversas tendencias conceptualizadas están los trabajos cuya postura afirma que el sector financiero es un elemento fundamental para el crecimiento de un país, entre los cuales se puede mencionar a Schumpeter (1912), McKinnon (1973), Jung (1986), Demetriades y Luintel (1996), Arestis y Demetriades (1997), entre otros (Levine, 2004).

La identificación y el análisis de las interrelaciones entre el desarrollo financiero y el crecimiento económico es un importante problema en la actualidad. El interés particular queda constituido en las interacciones dinámicas temporales entre las variables de interés, las cuales ayudan a determinar el mecanismo causal de un sistema subyacente y realizar pronósticos.

Un problema común consiste en determinar si los cambios en una variable son causa de la variación en otra. Con frecuencia en los trabajos empíricos se omite esta suposición y se procede directamente a realizar pruebas buscando relación entre variables. Encontrándose en el campo econométrico multitud de aplicaciones con elevadas correlaciones entre variables que no son más que relaciones espurias o carentes de significado económico.

El concepto probabilístico de causalidad está basado en la idea de que en el tiempo la causa siempre precede a los efectos. Si una serie de tiempo causa a otra, el conocimiento del primer proceso ayudaría a predecir los valores futuros del otro, después de que hayan sido tomadas en cuenta las influencias de otras variables. Sin embargo, debido a que el concepto no cuenta con una especificación a priori de un modelo causal, es particularmente adecuado para investigaciones empíricas tener una medida de asociación.

Granger (1969) fue el primero en proponer un test de causalidad, bajo el criterio de que el futuro no puede afectar al pasado, sino que en cualquier caso podría ser al revés. De esta forma, si una variable retardada está correlacionada con valores futuros de otra variable, se dice que una variable es causa de la otra según Granger. Decir que solo por eso existe causalidad no es correcto, ya que es posible que una variable retardada se correlacione espuriamente con otra variable solo porque es un indicador adelantado, y no porque exista verdadera causalidad, sobre todo si son series temporales no estacionarias; pero esta es una limitación que debe suplirse con la razón y la literatura y, en cualquier caso, lo que sí puede decirse es lo contrario, si no existe dicha correlación entonces la variable retardada no causa a la otra (Montero, 2013).

La idea intrínseca en estas pruebas es muy simple. Si X causa a Y, entonces los cambios en X deben preceder a los cambios en Y, o de forma equivalente si los coeficientes de la variable X retardada son significativos estadísticamente. En la práctica, lo habitual es encontrarse con una doble causalidad: X causa a Y e Y causa a X. No obstante es importante resaltar que la afirmación X causa a Y, no implica que Y sea el efecto o el resultado de X, pues intervienen además, otros factores al margen de X (Pindyck y Rubinfeld, 2001).

Dentro de este contexto, en el presente trabajo se muestra evidencia empírica sobre la causalidad entre el desarrollo del sector financiero y el crecimiento económico para los países de América del Norte: Canadá, Estados Unidos y México. El objetivo del trabajo es determinar si existe en estos mercados una relación entre el sector financiero representado por los índices de las bolsas de valores, y variables de la economía real representada por el PIB, M2, M3 y la tasa de interés libre de riesgo; asimismo, se busca la posibilidad de una interrelación entre los tres países, identificando la posible dirección de la causalidad entre las variables a través de un análisis de causalidad en el sentido de Granger y las pruebas extendidas de Granger, Toda y Yamamoto.

En orden de examinar las situaciones anteriormente planteadas, se consideraron las siguientes hipótesis: 1) el sector económico causa el desarrollo del sector financiero de cada país miembro del área del Tratado de Libre Comercio de América del Norte (TLCAN), y 2) el sector económico de Estados Unidos causa el desarrollo financiero de cualquiera de los países miembro del área del TLCAN.

Este trabajo se estructura de la siguiente forma: la primera sección presenta una revisión de los aspectos teóricos generales existentes; y en la segunda sección se analiza la causalidad en el sentido de Granger y las pruebas econométricas desarrolladas por Toda y Yamamoto para las diversas variables reales y financieras de las economías del área del TLCAN.

2. Revisión de la literatura

2.1. Teoría sobre crecimiento económico y desarrollo financiero

La relación entre el desarrollo financiero^[1] y crecimiento económico ha sido ampliamente discutida. Está bien identificado que el desarrollo financiero es crucial para un crecimiento económico y viceversa. Diversos estudiosos, como Schumpeter (1912), han reconocido esta relación de suma importancia.

Velázquez y Hernández Veleros (2013) explican que en el modelo de equilibrio general de Arrow-Debreu por la ausencia de dinero, pero principalmente al suponerse costos nulos de información y transacción, resulta innecesario el sistema financiero, por lo que su estudio queda relegado del modelo base de la teoría neoclásica. Si se permiten los costos de información y transacción hace necesaria la intermediación del sistema financiero para vincular a los oferentes y demandantes de fondos prestables. Para explicar esto presentan un esquema donde el sistema financiero influye sobre el sector real de la economía a través la vinculación de los ahorros de las familias con los requerimientos de fondos prestables para financiar la inversión que realizan las empresas. Así, se transforman los ahorros de las familias en créditos para las empresas y se decide a que actividades productivas financiar y a cuáles no. En este sentido, aclaran refiriendo que para Schumpeter (1912 citado en Levine, 1997, p. 695): “el oficial bancario no es, principalmente, un intermediario […] Autoriza a los individuos en nombre de la sociedad […] (para innovar)”.

En este sentido, Pagano (1993) plantea como explicación de la relación entre sistema financiero y crecimiento económico que la teoría neoclásica del crecimiento explicaba a la tasa de crecimiento a través de variables exógenas, por lo que no había forma que el funcionamiento del sistema financiero pudiera influir en ésta. Así el estudio del sistema financiero tuvo que esperar al surgimiento de la teoría de crecimiento endógeno de Romer y de Lucas. Por su parte Levine (1997) propone una nueva forma de estudiar la relación sistema financiero-crecimiento económico, la cual es denominada funcional, pues resalta cómo las funciones del primero impactan en el crecimiento.

De acuerdo con Guzmán, Leyva y Cárdenas (2007), la relación sistema financiero-crecimiento económico puede ser presentada de dos maneras: en primer lugar, el grado de desarrollo del sector financiero mejora la asignación de recursos entre proyectos. Esto se debe a que los mercados desarrollados promueven un mejor análisis de la información, lo que permite elegir entre proyectos más rentables aumentando la productividad del capital, y con ello, el crecimiento económico. Y en segundo lugar, el mercado financiero mejora la elegibilidad de los proyectos mediante la diversificación de riesgos. Si el mercado se encuentra más desarrollado pueden financiarse inversiones de alta rentabilidad, aunque los proyectos sean menos líquidos y más riesgosos. Sugiriendo con ello la existencia de complementariedad entre la capitalización del mercado financiero y la tecnología. Por tanto, la existencia de una relación, entre el desarrollo financiero y el crecimiento económico, se sustenta en el hecho de que un aumento en la capitalización del mercado, permitiendo a las empresas un fácil acceso a fuentes de financiamiento, resulta en un aumento en la productividad de todos sus factores, impulsando con ello el crecimiento económico (Pollack y García, 2004). Sin embargo, la discusión académica se ha centrado en torno a dos cuestiones: a) la existencia de la relación entre desarrollo financiero y crecimiento económico y b) la naturaleza y dirección de la relación entre ambas variables.

De manera general, según el estudio de Levine (2004), se puede citar que la literatura existente relacionada con este tema ha sido clasificada en función de la importancia del sector financiero para el crecimiento. Autores como Schumpeter (1912), Goldsmith (1969), McKinnon (1973), Shaw (1973), Jung (1986), King y Levine (1993), Arellano (1993), Odedokun (1996), Demetriades y Luintel (1996), Demetriades y Hussein (1996), Arestis y Demetriades (1997), Naranjo (1997), Levine y Zervos (1998), Demetriades y Luintel (2001), Guiso, Sapienza y Zingales (2004), Shen y Lee (2006), López y Rodríguez (2010), entre otros, encuentran evidencia contundente para respaldar la relación existente entre estas dos variables en un sentido o en el otro. No obstante, a pesar de la gran cantidad de literatura desarrollada en este tema, los trabajos antes citados no especifican el sentido o la dirección de la causalidad entre las variables de ambos sectores.

2.2. Estudios empíricos acerca de la relación entre crecimiento económico y desarrollo financiero

En su trabajo seminal Goldsmith (1969 citado en Levine, 2004), reconoce la importancia que tiene el efecto de la estructura financiera,^[2] y el desarrollo en el crecimiento económico. Recopilando datos de 35 países para el periodo comprendido de 1860 a 1963, mostró que el tamaño del intermediario financiero en relación con el tamaño de la economía aumenta a medida que los países se desarrollan, documentando gráficamente una correlación positiva entre el desarrollo financiero y el nivel de actividad económica.

Posteriormente se ha publicado una extensa cantidad de literatura donde se examina la relación entre el desarrollo financiero y crecimiento económico utilizando un sin número de pruebas econométricas. En el caso de Jung (1986) y Demetriades y Hussein (1996), citados en Levine (2004), emplean como medidas del desarrollo financiero el ratio del dinero al PIB, encontrando que la dirección de la causalidad frecuentemente va en ambas direcciones, especialmente para aquellos países desarrollados. Greenwood y Jovanovic (1990 citado en Levine, 2004), plantean en un modelo no lineal la manera como la interacción entre el desarrollo financiero y económico puede dar lugar a una curva en forma de U de desigualdad entre el ingreso y el desarrollo de los intermediarios financieros.

King y Levine (1993 citado en Levine, 2004), realizan un estudio en 77 países para el periodo de 1960 a 1989, construyendo medidas adicionales del nivel de desarrollo financiero y analizando si el nivel de desarrollo financiero prevé un crecimiento económico de largo plazo, la acumulación de capital y crecimiento de la productividad. Estos autores encontraron resultados, ignorando la causalidad de los mismos, consistentes entre los diferentes indicadores del desarrollo financiero que indican la existencia de una fuerte relación positiva entre cada uno de ellos con los indicadores de crecimiento, la tasa de crecimiento a largo plazo del PIB per cápita, la acumulación de capital y el crecimiento de la productividad.

Neusser y Kugler (1998 citado en Cermeño et al., 2006), encontraron que el sector financiero estimula el crecimiento. Por su parte Rousseau y Wachtel (1998 citado en Levine, 2004), documentaron que la dirección dominante de causalidad va del desarrollo financiero al crecimiento económico.

Demirguc-Kunt y Maksimovic (1998 citado en Levine, 2004), utilizan variables para medir el desarrollo financiero como la capitalización del mercado y la rentabilidad del total de las acciones en el mercado. Posteriormente, Levine y Zervos (1998 citado en Levine, 2004), construyen numerosas medidas del desarrollo del mercado de valores para evaluar la relación entre este y el crecimiento económico, la acumulación de capital y el crecimiento de la productividad en una muestra de 42 países durante el periodo de 1976 a 1993.

Los resultados de Levine y Zervos (1998) son consistentes con aquellos desarrollados sobre la hipótesis acerca de que la liquidez del mercado de valores facilita el crecimiento a largo plazo. Ellos muestran que la liquidez inicial del mercado de valores y el nivel inicial del desarrollo bancario, crédito bancario, están positiva y significativamente correlacionados con las futuras tasas de crecimiento económico, la acumulación de capital y crecimiento de la productividad en los próximos 18 años, incluso después de controlar el ingreso inicial, la escolaridad, la inflación, el gasto público, la prima del tipo de cambio en el mercado negro y la estabilidad política. Sin embargo, ellos no especifican la dirección de la causalidad entre estas variables. Por su parte Arestis, Demetriades y Luintel (2000), en Levine (2004), encontraron evidencia adicional que soporta la hipótesis de que el desarrollo financiero estimula el crecimiento, pero plantean algunas precauciones en cuanto al tamaño de la relación.

Algunos autores se han apoyado en modelos econométricos sofisticados para tratar esta relación entre el sector financiero y el sector real. Xu (2000 citado en Levine, 2004), utilizando un Modelo de Vectores Autorregresivos (VAR), rechazó la hipótesis de que el sector financiero simplemente sigue el crecimiento. Más allá, su análisis indica que el desarrollo financiero es importante para el crecimiento a largo plazo.

Guiso, Sapienza y Zingales (2002 citado en Cermeño et al., 2006), examinaron los efectos del desarrollo financiero en actividades económicas para las regiones de Italia. Sus resultados indican que el desarrollo local financiero otorga posibilidades económicas reales a los empresarios para iniciar sus negocios, incrementando la competencia industrial y promoviendo el crecimiento de las empresas. Estas evidencias no son adjudicables para grandes empresas, quienes fácilmente pueden obtener recursos fuera de las áreas locales.

Fink, Haiss y Hristoforova (2003 citado en Levine, 2004), utilizando pruebas de causalidad de Granger y métodos de cointegración, examinaron el impacto del desarrollo del mercado de bonos sobre la producción real en trece economías desarrolladas para el periodo de 1950 a 2000. La evidencia encontrada por estos autores indica que el desarrollo del mercado de bonos influencia la actividad de la economía real.

Calderón y Liu (2003), empleando pruebas de descomposición de Geweke, encontraron que: 1) el desarrollo financiero en general conduce al crecimiento económico; 2) la causalidad de Granger del desarrollo financiero al crecimiento económico y la causalidad de Granger del crecimiento económico al desarrollo financiero coexiste; 3) la profundización financiera contribuye más a las relaciones causales en los países en desarrollo que en los países industrializados; 4) entre mayor es el intervalo de muestreo, mayor será el efecto del desarrollo financiero sobre el crecimiento económico; y 5) la profundización financiera impulsa el crecimiento económico a través de una acumulación de capital más rápida y el crecimiento de la productividad.

Christopoulos y Tsionas (2004 citado en Levine, 2004), encontraron fuerte evidencia en favor de que la hipótesis sobre la dirección de la causalidad a largo plazo va en sentido del desarrollo financiero al crecimiento económico y no encuentran evidencia de causalidad en ambos sentidos. Levine (2004) apunta la relación existente entre las finanzas, la distribución del ingreso y la pobreza. Precisa que la relación entre finanzas y la distribución del ingreso es relevante para entender el proceso del desarrollo económico y, a la vez, señala que esta indirectamente relacionada al crecimiento, debido a que la distribución del ingreso puede influenciar decisiones de ahorro, de asignación de recursos, de incentivos para innovar y de políticas públicas.

El trabajo de Hassana, Sánchez y Yuc (2011) pone de manifiesto evidencia sobre el papel del desarrollo financiero para el crecimiento económico en los países de bajos y medianos ingresos, clasificados por regiones geográficas. Ellos encontraron una relación positiva entre el desarrollo financiero y el crecimiento económico en los países en desarrollo. Por otra parte, el análisis multivariado de corto plazo ofrece resultados mixtos: a) una relación de causalidad bidireccional entre el sector financiero y el crecimiento de la mayoría de las regiones y b) la causalidad de un solo sentido del crecimiento a la financiación para las dos regiones más pobres.

Para el área de América del Norte también existe literatura haciendo referencia a la relación causal entre el desarrollo del sector financiero y el crecimiento económico. Los resultados del trabajo de Gopinath, Kennedy y Roe (1995) indican la importancia tanto del crecimiento de los avances tecnológicos como de los términos de intercambio para el bienestar en los tres países. Un análisis del crecimiento de los avances tecnológicos sugiere que la mayor apertura de la economía mexicana aumenta este efecto a través de, por ejemplo, el aumento de las importaciones de factores intermedios más modernos, mientras que, para las economías más abiertas, los efectos comerciales del TLCAN son pequeños.

Para Hernández y Robins (2000) el mercado accionario mexicano causa, en el sentido de Granger, al crecimiento económico medido por la producción industrial. De igual forma, estos autores concluyen que la oferta monetaria (M1) causa en el sentido de Granger al mercado accionario y a la producción industrial. Ellos no encontraron evidencia significativa sobre la causalidad de la tasa de interés de los Cetes a 28 días, el tipo de cambio y la inflación sobre el desarrollo financiero. Sin embargo, en la prueba acerca de la relación entre las variables económicas y financieras de la economía de Estados Unidos afectando a los rendimientos de la Bolsa Mexicana de Valores (BMV), encontraron causalidad de Granger que confirma que la tasa del Tesoro de Estados Unidos (T-Bills) causa a los rendimientos de la BMV, y no rechazaron la hipótesis de no causalidad de Granger sobre el Índice Dow Jones hacia el mercado mexicano.

En el trabajo desarrollado para el caso de México, Ortiz, Cabello y De Jesús (2007) encontraron que, para el periodo comprendido de 1968 a 2002, existe causalidad de Granger en ambos sentidos en la relación entre el mercado de valores y el crecimiento económico. Mientras que Hurlin y Venety (2008) rechazaron la hipótesis nula de no causalidad homogénea cuando investigaron la relación causal del crecimiento económico con el desarrollo financiero para 28 países desarrollados, entre los cuales figuran Canadá, México y Estados Unidos.

En la evidencia empírica encontrada por Gries, Kraft y Meierrieks (2008), para el caso de México, los autores destacan que el desarrollo financiero sigue al crecimiento económico. López y Rodríguez (2010) encontraron para México evidencia de una causalidad débil, en el sentido de Granger al nivel de significación de 10%, que va del sector financiero (representado por el índice accionario de la bolsa), al sector económico (representado por el Índice de Volumen de la Producción Industrial). Y Garza y Vera (2010) estudiando la influencia de las variables macroeconómicas de China y Estados Unidos sobre los mercados de valores de América Latina, descubrieron que las variables macroeconómicas de Estados Unidos causan en el sentido de Granger a la Bolsa Mexicana de Valores.

El debate sobre la dirección de la causalidad entre el desarrollo financiero y el crecimiento económico ha crecido ampliamente desde la década de 1980 en la literatura teórica y empírica. La literatura existente ofrece opiniones contrarias de esta relación. Por esto, una correcta metodología econométrica no puede ser mecanicista pues, como ya señaló Amemiya (1980 citado en Guisán, 2002), la investigación econométrica de calidad es una mezcla de ciencia y arte que se basa en la profundidad del pensamiento, en el grado de conocimiento de la realidad económica y del pensamiento de otros autores, y en la capacidad de relacionar los efectos con sus causas; y por tanto, se deben utilizar las pruebas de causalidad adecuadas en función de si las series son o no estacionarias. En este sentido, el presente trabajo ha detectado que en muchas investigaciones no se hace previamente el análisis de estacionariedad y se aplican pruebas no adecuadas.

2.3. Modelos causales y estadísticos de contraste

Dado los resultados empíricos tan diversos en la literatura se hace necesario reexaminar para las economías objeto de estudio las relaciones causales entre el sector financiero, expresamente el mercado de valores, y la economía real. Por ello, a modo de resumen se rescatan las características principales del método de causalidad de Granger.

El método de causalidad de Granger, según Zuñiga (1992), es una herramienta estadística para determinar el sentido de la relación entre las variables. A diferencia del coeficiente de correlación que mide el grado de asociación entre pares de variables sin importar que estas tengan una relación de dependencia. El concepto de causalidad de Granger hace referencia a la precedencia de una variable sobre otra variable. Este concepto sostiene que si xt puede ser explicado por sus valores pasados y por los valores pasados de yt, entonces yt causa a xt; es decir, cuánto del valor observado de xt puede ser explicado por los valores pasados de xt y de yt.

Granger presentó la prueba de causalidad en 1969 de la siguiente manera:

Donde:

A₀ = es un conjunto de matrices;

m = puede ser infinita;

ε_t = es la parte no explicada del modelo que se incluye como un vector de variables aleatorias llamadas ruido blanco, las cuales toman los valores E [ε_t’, ε_s] = 0 si t ≠ s; y E [ε_t’, ε_s] = I si t = s.

Según Granger, este modelo puede ser ilustrado para el caso de dos variables xt y yt:

Donde:

y_t no causa a x_t si b_j = 0 j ; y x_t no causa a y_t si Cj =0 j.

En términos simples, la prueba de Granger establece que si X causa a Y, entonces cambios en X deben preceder a cambios en Y. En particular, si X causa a Y significa que X debe ayudar a predecir Y, pero Y no debería contribuir a predecir X. Si X ayuda a predecir Y, esto significa que en una regresión de Y en función de los valores pasados de Y, la adición de valores pasados de X como variables independientes deben contribuir significativamente al poder explicativo de la regresión.

La prueba de la hipótesis nula, donde X no causa a Y en términos de Granger, se puede realizar mediante la comparación de una regresión irrestricta y de una restringida. La primera está determinada en función de los valores rezagados de Y y de X, mientras que la segunda está dada en función de los valores rezagados de Y. Debido a que esta prueba debe ser analizada en ambas direcciones, la hipótesis nula donde Y no causa a X, puede ser examinada de forma similar. De esta manera, al rechazar una de las dos hipótesis se puede concluir qué variable causa a la otra (Zuñiga, 1992).

Para definir causalidad, Granger (1988) utiliza la distribución condicional de xt, dados los conjuntos de información J y J’:

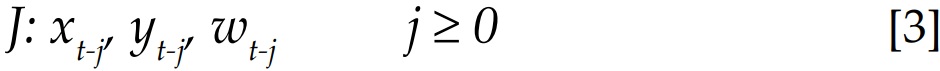
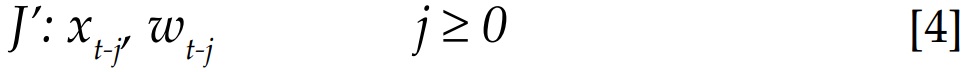
Donde:

X_t-j, y_t-j, w_t-j = son elementos de los vectores: x_t, y_t, y w_t; J = denota toda la información disponible al igual que J’ pero esta excluye la información del pasado y del presente de yt.

Para Granger y_t causa a x_t-1 cuando f(x_t+1 J) ≠ f(x_t+1 J’); y no causa si f(x_t+1 J) = f(x_t+1 J’). La definición de causalidad implica que si y_t causa a x_t, entonces x_t+1 es mejor predictor cuando se utiliza a y_t-j que cuando no se hace así.

Diebold (1998) argumenta que “una serie causal debe contener información útil para el pronóstico que no este disponible en las demás series (incluyendo la historia pasada de las variables pronosticables)”. La definición de causalidad de Granger se basa en dos principios fundamentales: 1) la causa ocurre antes que el efecto; y 2) la serie causal contiene información acerca de la serie causada que no está disponible en otras series, aquí llamada w_t.

En este sentido, Granger (1987) define los conceptos de integración y cointegración, y destaca las diferencias de una variable integrada de orden cero y de orden mayor o igual a uno como se muestra a continuación:

• a) Integración. Una serie con componente no determinista, la cual es estacionaria e invertible, y que tiene una representación ARMA después de diferenciarla d veces, se llama integrada de orden d y se expresa como x_t ≈ I(d).

  b) Integración de orden cero. Si x_i ≈ I(0), entonces la varianza de x_i es finita, las innovaciones tienen un efecto temporal sobre el valor de x_t y las autocorrelaciones decrecen en una magnitud K por lo cual su suma es finita.

  c) Integración de orden uno. Si x_t ≈ I(1), entonces la varianza es infinita, las innovaciones tienen efectos permanentes sobre el valor de x_t y las autocorrelaciones teóricas K para t tienden a infinito.

  d) Cointegración. Aunque dos series (x_t y y_t) individualmente sean I(d), puede existir entre ellas una combinación lineal z_t = x_t + ay_t integrada de orden cero (estacionaria), si esto ocurre se dice que ambas series están cointegradas o que hay una relación cointegrante entre ellas.

Granger (1988) propuso una prueba para estudiar la causalidad de series temporales. Sin embargo, esta no es una prueba en un sentido filosófico y se debe entender más como un sentido de predeterminación entre las variables, por ejemplo, una variable podría ser predeterminada por otra. En consecuencia, la causalidad dinámica de la prueba de causalidad de Granger puede obtenerse a través del modelo VAR, pero se trata de variables integradas, y la aplicación estándar de la prueba de causalidad de Granger, en tal caso, es inválida. Además, Granger recomienda realizar pruebas de integración y cointegración de las series antes de probar causalidad porque si las series son integradas de orden d ≥ 1 y están cointegradas, entonces los modelos para probar causalidad deben incluir métodos de corrección del error (Granger, 1988).

Granger (1988 citado en Muñoz y Vindas, 1995), remarcó que, sobre la base de la representación de corrección de error en el caso de variables cointegradas, puede suceder que las pruebas de causalidad aplicadas después de diferenciar las variables para alcanzar estacionariedad no sean adecuadas debido a que abandonan la información derivada del error de equilibrio. Así el modelo de corrección de error provee un punto de referencia para extender las pruebas de causalidad.

En el caso de variables cointegradas existen dos vías en las cuales la variable Y_t ayuda a predecir la variable X_t: primero por medio de la información pasada de Y_t; y segundo por medio del término Y_t-1 que contiene el término de error de equilibrio Z_t-1. Específicamente, para un modelo de dos variables se tiene el siguiente sistema:

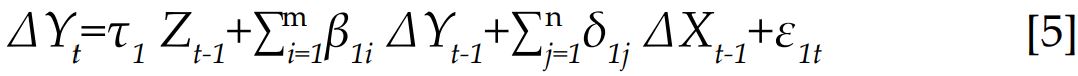
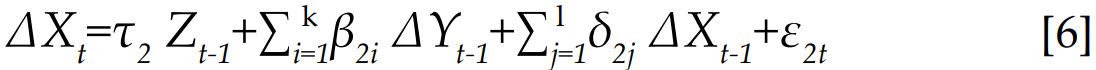
Estas ecuaciones corresponden a la representación autorregresiva para variables integradas de primer orden pero con un vector agregado que corresponde a corrección de error (Z_t-1= Y_t-1- a X_t-1).

Para probar la hipótesis Ho: Y no causa a X y para una particular identificación del número de rezagos, se formulan dos especificaciones para la segunda ecuación del modelo de corrección error: Ecuación sin restricción (SS):

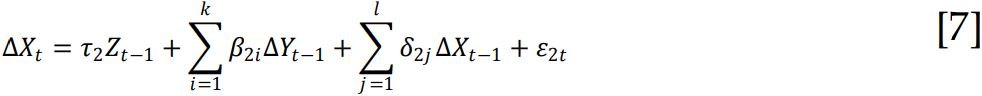
y ecuación con restricción (SSc):

Z_t-1 es el error de equilibrio, computado como el residuo de la ecuación de cointegración correspondiente. En tanto que la segunda ecuación está formulada sobre la hipótesis de que Y no es causa de X.

Sobre la hipótesis de que los residuos e_2tc» iid (0,s) y considerando que las variables son estacionarias, el resultado del modelo de regresión lineal corresponde al caso de la regresión estocástica cuando hay independencia contemporánea. En el caso de los estimadores MCO, estos son consistentes y asintóticamente normales con la varianza asintótica usual. No es posible aplicar pruebas exactas para probar la hipótesis de que H_o=G₂=ß₂=...=G₂=d₂₁=...=d2l=0 (o equivalentemente de que Y no causa a X). El estadístico F usual no puede ser aplicado porque no tiene la distribución F-Snedecor (ni el numerador ni el denominador tienen la distribución Chi-cuadrado necesaria). Sin embargo, es posible usar pruebas asintóticas (Muñoz y Vindas, 1995).

Algunas de las condiciones que señala la literatura econométrica para desarrollar pruebas extendidas de causalidad son: el principio de Wald, el de máxima verosimilitud y el multiplicador de Lagrange. Geweke (1983 citado en Muñoz y Vindas, 1995), con base en el método directo de Granger y suponiendo estacionaridad de X e Y, normalidad de los errores y una identificación del número de rezagos (un rezago para X y k rezagos para Y), formula los siguientes estadísticos para las ecuaciones con y sin restricciones:

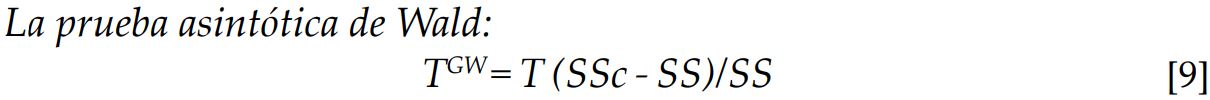
Donde:

T: número de observaciones,

SS: suma de los errores al cuadrado de la ecuación sin restricción,

SSc: suma de los errores al cuadrado de la ecuación con restricción.

Los estadísticos anteriores, sobre la hipótesis de no causalidad de Y a X, tienden a cero. La distribución de cada estadístico converge hacia la distribución Chi-cuadrado, con (p+1) grados de libertad.

En ese sentido, Toda y Yamamoto (1995) han sugerido un procedimiento alternativo para determinar la causalidad sin realizar pruebas preliminares de cointegración. Cuando las variables están integradas, estos autores proponen estimar un modelo VAR con (k + d_max) rezagos, donde k es el número óptimo de rezagos en el VAR y d_max es el número de orden máximo de integración que ocurre en el proceso; y los términos de error son ruido blanco con media cero, varianza constante y no autocorrelación. Una vez estimado el VAR, prueban la causalidad de Granger pero únicamente utilizando los primeros k rezagos. La prueba considera la siguiente ecuación de un modelo VAR:

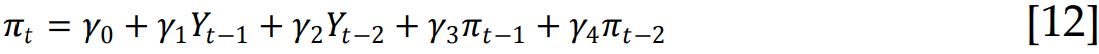
Donde k = 1 puede ser seleccionado de acuerdo con el criterio Akaike (AIC) o Schwarz (SIC) y d_max = 1, entonces, la hipótesis nula de no causalidad de Y a π es: H₀:γ1=0. Esto es, H₀: X no causa en el sentido de Granger a Y.

Además, utilizando las ecuaciones con y sin restricción de Granger (1988), Toda y Yamamoto (1995) calculan el estadístico F para la prueba modificada de Wald:

Donde K es el número de coeficientes estimados. El estadístico de la prueba es asintótico χ² con m grados de libertad, siendo estos el número de restricciones. Lo interesante de esta prueba es que el resultado se mantiene sin importar si Xt es I (0) o I (1) y si existe cointegración (Lin, 2008).

Giles (2013) abordando la prueba de Toda y Yamamoto (TY), enfatiza que si se está utilizando una prueba de Wald para examinar restricciones lineales en los parámetros de un modelo VAR y alguno o varios de los datos son no estacionarios, entonces el estadístico de Wald no sigue la distribución asintótica habitual de Chi-cuadrado bajo la hipótesis nula. Por lo tanto, no se puede aplicar la prueba de Granger de la forma habitual, ya que la distribución asintótica del estadístico conlleva parámetros de ruido que no se pueden observar, por lo que es totalmente no estándar. Es en estos casos cuando se debe utilizar el procedimiento de TY.

Oxley y Grasley (1998) señalan que la prueba puede realizarse de las siguientes formas: a) correr un modelo que incluya rezagos, entre 3 y 5, cuando las variables son estacionarias, o siendo no estacionarias que estén cointegradas. Y b) correr el modelo entre las variables en diferencias, previa corrección de la correlación mediante un modelo de corrección de errores.

En Villegas (2012) se muestra una aplicación de la prueba extendida de causalidad de TY para encontrar la dirección de la causalidad entre el crecimiento económico de México y la Inversión Extranjera Directa (IED). Montero (2013) resalta la importancia inherente en cualquiera de los dos modelos en la determinación del número de rezagos a incluirse. Para ello recomienda, en primera instancia, utiliza la razón en función de la naturaleza temporal de los datos. Para luego realizar una regresión lineal e introducir rezagos en tanto crezca el coeficiente de determinación (R²) ajustado.

3. Metodología

Retomando los resultados obtenidos en diversos trabajos realizados con anterioridad acerca de la relación entre el sector financiero y el crecimiento económico, se utilizaron las series de tiempo con mayor frecuencia de aparición en dichos trabajos. Como variables proxies del sector real de cada país se eligieron: el PIB, M2, M3 y la tasa de interés a corto plazo. En tanto que para estimar la actividad del mercado bursátil se usaron los índices de las bolsas de valores de Canadá (TSX), Estados Unidos (S&P500) y México (IPC), respectivamente. Todas las variables fueron desestacionalizadas^[3] y transformadas en logaritmos neperianos para facilitar su incorporación en los programas econométricos Eviews 7.1 y J-Multi.

Los datos tienen una frecuencia trimestral para el horizonte temporal comprendido entre 1970 a 2011. Las series canadiense y estadounidense comprenden un total de 168 observaciones cada una de ellas. En el caso de México, la muestra se acorta por la disponibilidad de la información. El conjunto de series económicas y financieras se obtuvieron de la base de datos International Financial Statistics (IFS) del Fondo Monetario Internacional. Para determinar las relaciones causales se emplearon dos procedimientos: el modelo de Granger (1988) y la metodología extendida para la prueba de no causalidad de Granger de Toda y Yamamoto (1995).

4. Resultados

En la figura 1, con la finalidad de mostrar evidencia empírica de la relación existente entre el sector financiero y la economía real, se observa la dinámica de la evolución en el tiempo entre las variables canadienses. Como puede apreciarse las variables proxies tienden a moverse de manera conjunta, solamente las tasas de interés muestran una dinámica similar al mercado bursátil.

Para el caso de México, como se muestra en la figura 2, sucede algo diferente que en el caso del mercado canadiense. Las variables que reflejan la dinámica de la economía real parecen moverse de manera conjunta; excluyendo de este comportamiento a las tasas de interés y el desempeño del mercado de valores. Permitiendo inferir la inexistencia de alguna relación de largo plazo entre estas variables.

En tanto que para Estados Unidos, se puede observar en la figura 3 un comportamiento similar al del mercado canadiense. Destacándose en este sentido la existencia de alguna relación de largo plazo entre los parámetros.

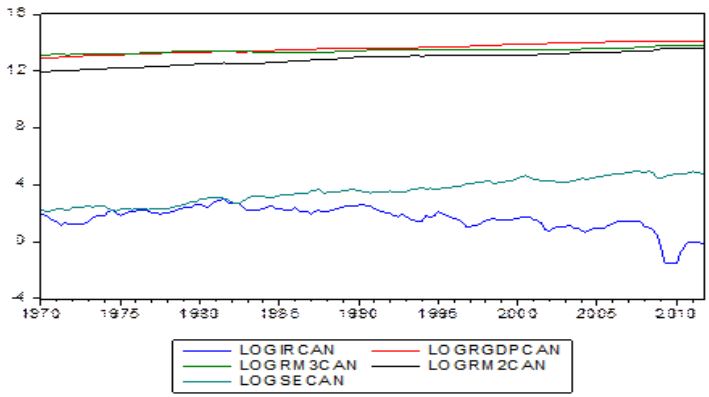
Figura 1
Comportamiento de la economía real y el mercado bursátil de Canadá, 1970-2011. Fuente: Elaboración propia a partir de datos obtenidos del IFS.

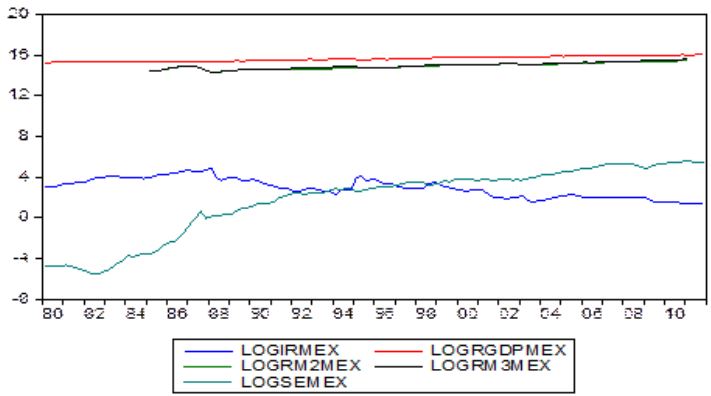
Figura 2
Comportamiento de la economía real y el mercado bursátil de México, 1970-2011. Fuente: Elaboración propia a partir de datos obtenidos del IFS.

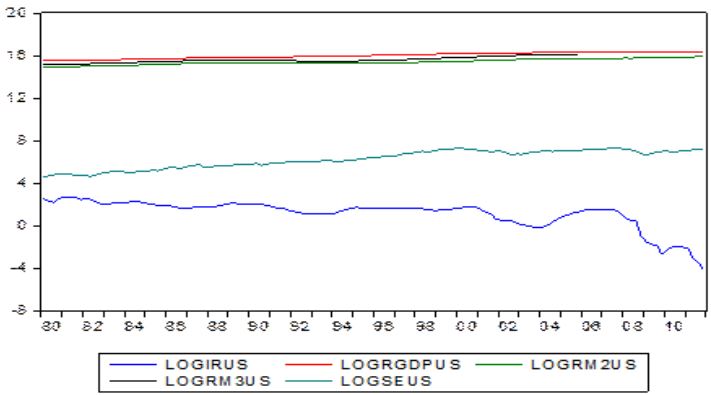
Figura 3
Comportamiento de la economía real y el mercado bursátil de Estados Unidos, 1970-2011. Fuente: Elaboración propia a partir de datos obtenidos del IFS.

Continuando con el procedimiento de Granger, se verificó el orden de integración de las series incorporadas en los modelos. Para ello se realizaron previamente las pruebas de Dickey-Fuller de raíces unitarias, en las cuales se contrasta la hipótesis nula de que la serie en cuestión es estacionaria y, por tanto, la hipótesis alternativa es que posee una raíz unitaria, los resultados se incorporan en el cuadro 1.

Cuadro 1

Prueba ADF

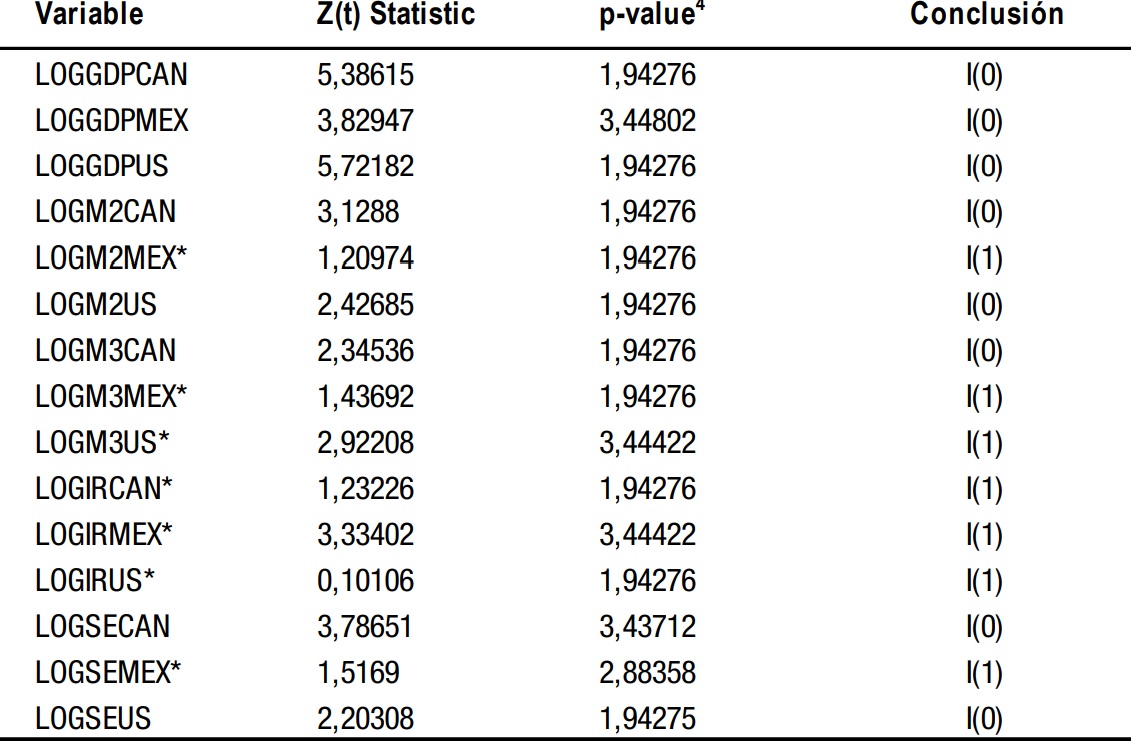
*Serie no estacionaria al 5% de nivel de significancia. (Datos analizados en E-Views 7.1)

[1] MacKinnon (1996).

Fuente: Elaboración propia a partir de datos obtenidos del IFS.

Cuadro 2

Número óptimo de rezagos por variable

Fuente: Elaboración propia a partir de datos obtenidos del IFS

Luego se verificó el número de rezagos significativos necesarios en cada variable, de acuerdo con el criterio de información de Akaike, como se muestra en el cuadro 2.

La metodología utilizada en el presente trabajo se sustenta en la construcción de Vectores Autorregresivos (VAR) de pares de variables del tipo:

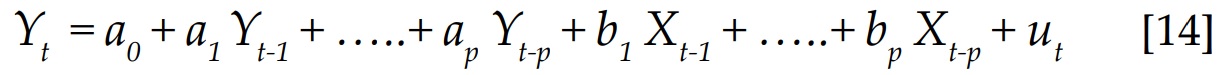
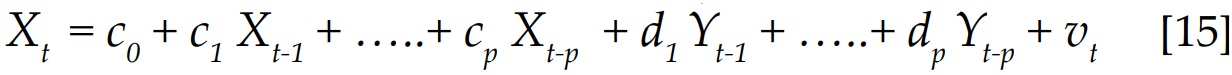
Para el análisis, las variables endógenas utilizadas para cada país fueron una variable proxy de la economía real y la variable del desempeño del sector financiero.

Después de haber definido los modelos VAR, se utilizó la prueba de causalidad de Granger para verificar el efecto entre pares de variables de los tres países objeto de estudio y así poder probar H₀: b₁ = b₂ = ... = p_b = 0, contra H_A: ‘N₀ H₀’, que es una prueba de que X no causa en sentido de Granger a Y.

De manera similar, probar H₀: d₁ = d₂ = ... = d_p = 0, contra H_A: ‘N₀ H₀’, es una prueba de que Y no causa en sentido de Granger a X. El rechazo de estas hipótesis nulas implica la existencia de causalidad de Granger.

Finalmente, los resultados de las pruebas econométricas de causalidad de Granger pareadas entre las variables de cada país, determinando la dirección de la causalidad entre ellas, se muestran a continuación en el cuadro 3.

Dado que el interés de esta investigación se centra en determinar si el crecimiento económico tiene algún impacto en el desarrollo del mercado financiero, se puede afirmar que a partir de la prueba de no causalidad de Granger existe evidencia significativa.

Para el caso del mercado canadiense, este se ve afectado por la dinámica de dos variables de la economía real de ese país: el PIB y M2. En cuanto al mercado financiero mexicano, este se ve influenciado por tres variables: M2, M3 y la tasa de interés. Es necesario resaltar que, para el mercado estadounidense, no se encontró evidencia de que la economía real de ese país cause el desarrollo del sector financiero.

Cuadro 3

Prueba pareada de No Causalidad de Granger

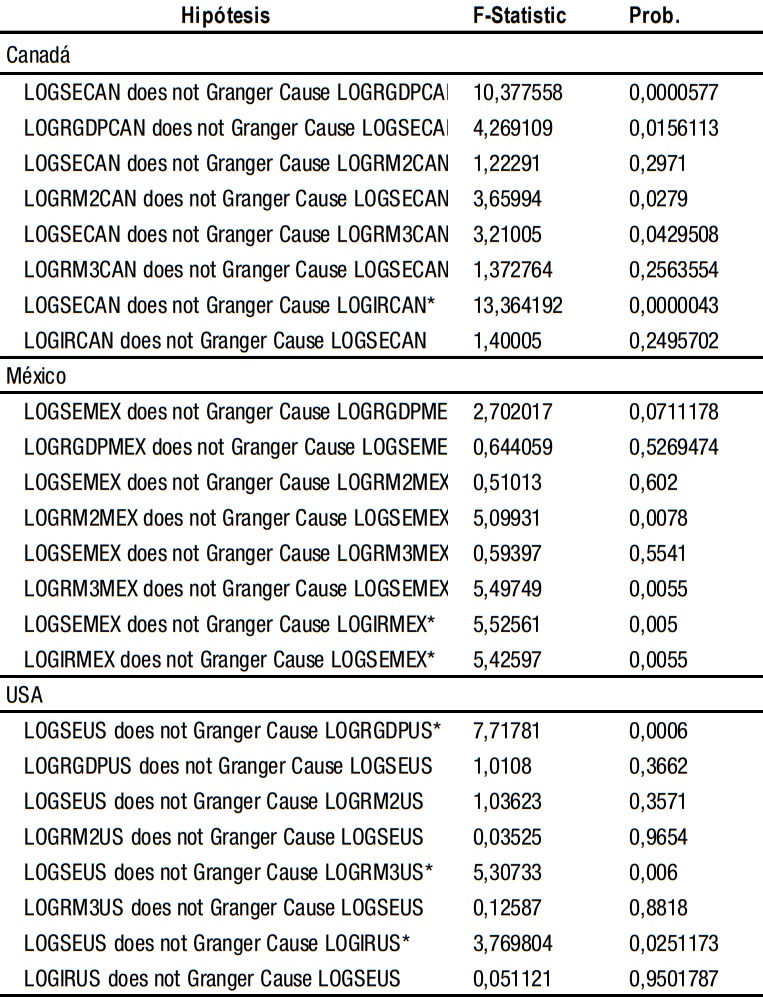
* Significativa al 95% de nivel de confianza.

Fuente: Elaboración propia a partir de datos obtenidos del IFS.

Lamentablemente los resultados obtenidos pueden ser erróneos debido a la presencia de series no estacionarias y rompimientos estructurales, por lo cual se debe asegurar con otros procedimientos que estos son válidos (Giles, 2013). Para ello se utilizó la metodología extendida de Toda y Yamamoto para la prueba de no causalidad de Granger.

Toda vez verificado el orden de integración de las series, se procedió a fijar el máximo orden de integración (M) para cada grupo de variables, el cual será utilizado posteriormente. En el cuadro 4 se muestran los resultados.

Cuadro 4

Máximo orden de integración por grupo de variables

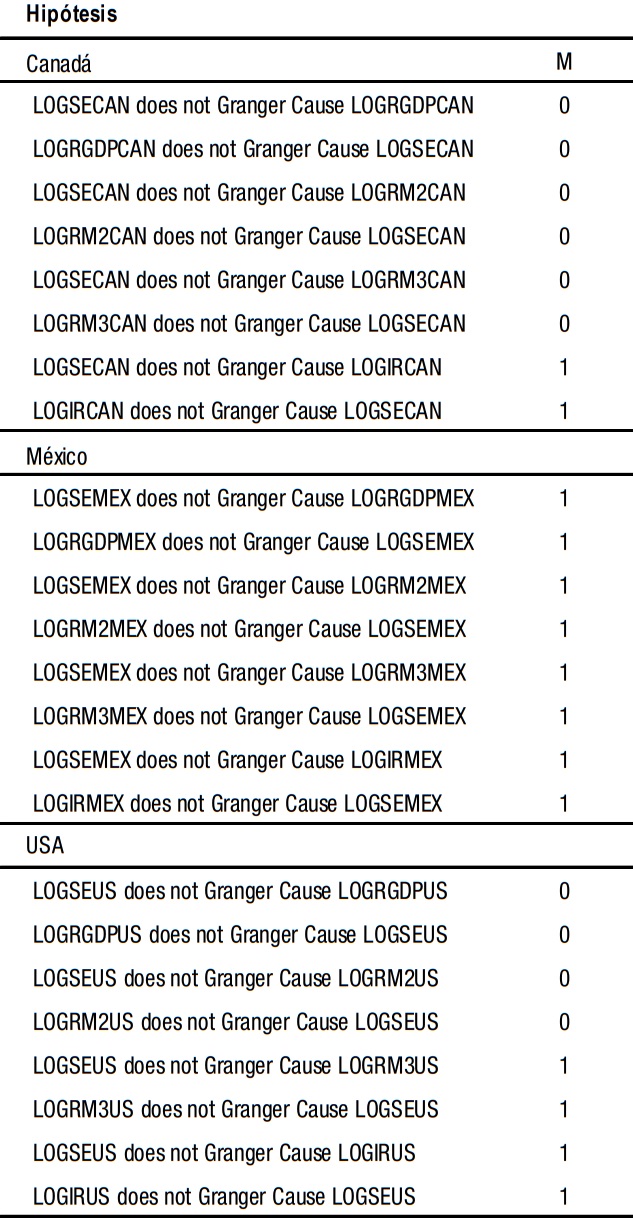
* Significativa al 95% de nivel de confianza.

Fuente: Elaboración propia a partir de datos obtenidos del IFS.

Después de haber definido el VAR, se contemplaron los números de rezagos adecuados para cada grupo de variables con base en el criterio de información de Schwarz,^[4][5] asegurando que el modelo no tuviera problemas de correlación en los residuos con la prueba del multiplicador de Lagrange, como se puede apreciar en el cuadro 5.

Cuadro 5

Prueba LM VAR Serial Correlation

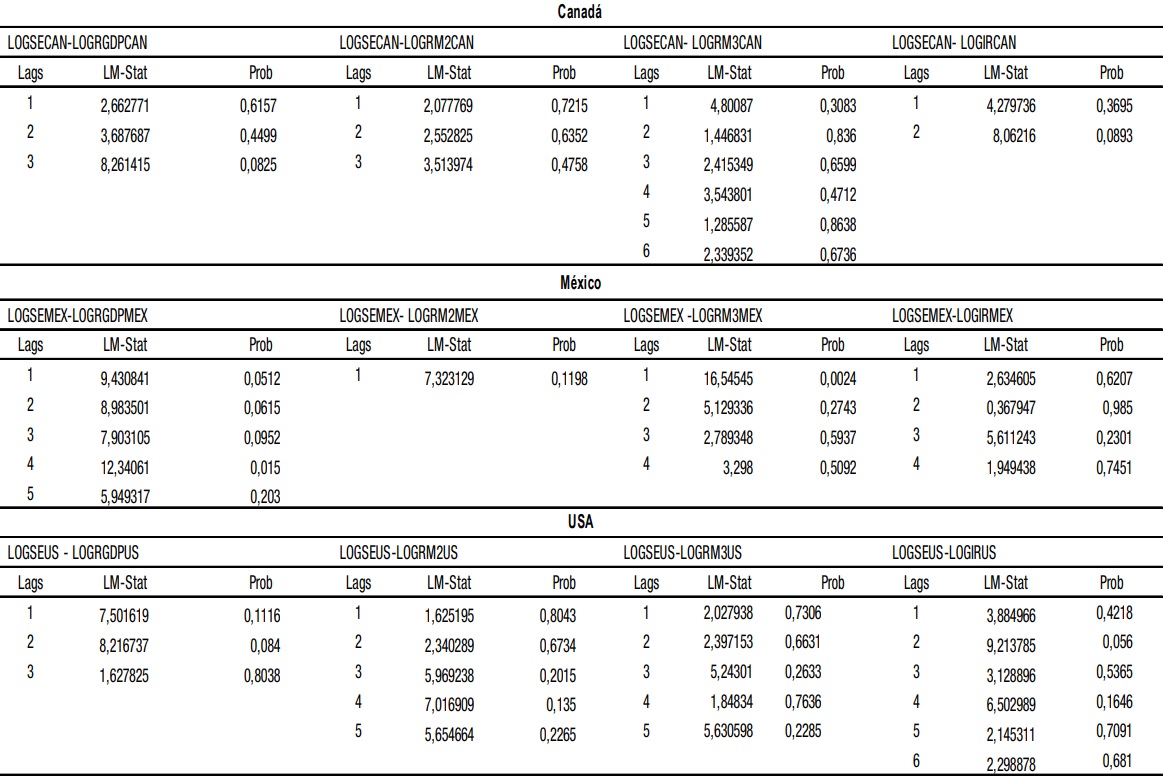
Fuente: Elaboración propia a partir de datos obtenidos del IFS.

El cuadro 6 presenta los resultados de la prueba de la traza contemplando los elementos determinísticos respectivos de los procesos generadores de esos datos, confirmado la presencia de vectores cointegrantes solo entre tres pares de las variables en cuestión: LOGSEMEX-LOGRGDPMEX, LOGSEMEX-LOGRM- 2MEX y LOGSEUS–LOGRGDPUS.

Sin importar los resultados obtenidos (Giles, 2013), ya que no afectan el procedimiento de Toda y Yamamoto, debido a que solo servirán de parámetro de comparación al final, se procedió a verificar la causalidad de Granger a través de la prueba de Wald, como se muestra en el cuadro 7.

Como se puede apreciar, la prueba permite rechazar la hi- pótesis nula de no causalidad en el sentido de Granger en doce de los treinta pares de variables en cuestión.

Cuadro 6

Prueba de la traza de Johansen

*Indica rechazo de la hipótesis nula al 5% de significancia.

**MacKinnon-Haug-Michelis (1999) p-values

Fuente: Elaboración propia a partir de datos obtenidos del IFS.

Cuadro 7

Pruebas de no causalidad en el sentido de Granger. (Prueba de Wald)

*Indica rechazo de la hipótesis nula al 5% de significancia.

Fuente: Elaboración propia a partir de datos obtenidos del IFS.

Dado que los resultados de esta prueba indican la causalidad en ambas direcciones y el interés central de este trabajo son los mercados financieros, se prioriza la direccionalidad que va de la economía real hacia el sector financiero. Encontrando, para el caso del mercado canadiense fuerte evidencia de que la causalidad va del PIB canadiense y de la Bolsa de Estados Unidos hacia la Bolsa de Canadá. En cambio, para el mercado mexicano el PIB de ese país y M3 lo causan; este último resultado coincide con la evidencia empírica proporcionada por Hernández y Robins (2000).

Es de resaltar que, a pesar de encontrarse vectores cointegrantes en la prueba de la traza previamente realizada entre tres pares de las variables en cuestión: LOGSEMEX-LOGRGDPMEX, LOGSEMEX-LOGRM2MEX y LOGSEUS–LOGRGDPUS, no se confirmaron las relaciones de causalidad en los casos de M2 para México y el PIB para Estados Unidos.

Con la finalidad de robustecer los resultados y conocer el efecto de un shock en la economía sobre los mercados accionarios, y viceversa, se calcularon las funciones de respuesta a impulso respecto a cada variable. Estas funciones permiten verificar el impacto del shock y medir el tiempo de afectación (Zavaleta y Urbina, 2011).

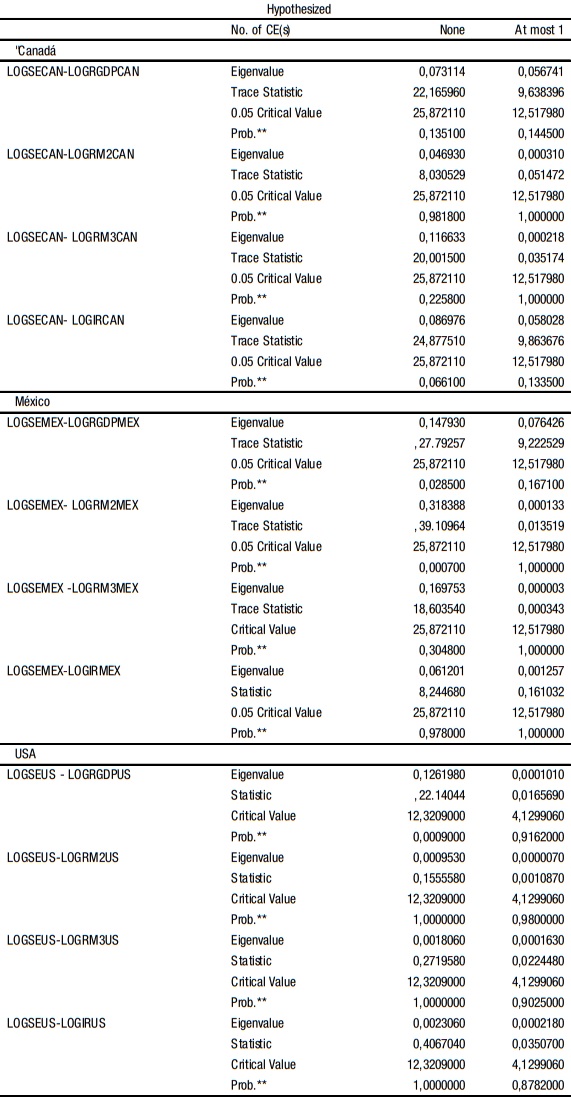
Un cambio en los errores de la ecuación de SECAN, del orden de una desviación típica del error de esta primera ecuación, como se observa en la figura 4, provoca un incremento equivalente a 0,012521 en el periodo inicial, aumentando a 0,019976 después de 6 periodos. A partir del séptimo periodo, los efectos tienden a crecer lentamente por arriba de 0,02.

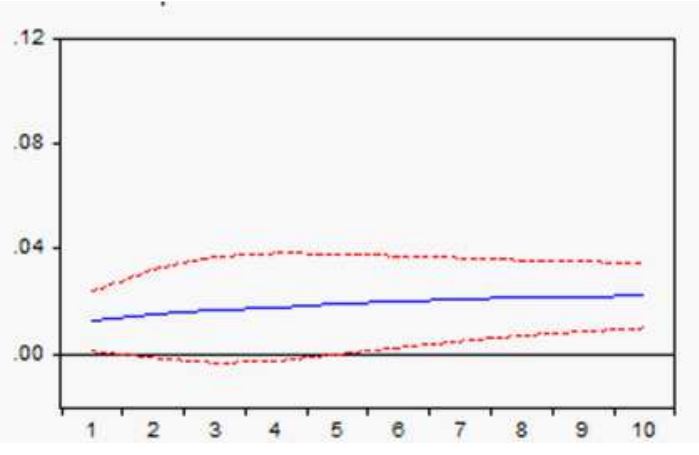
Figura 4
Respuesta a impulso de la Bolsa de Canadá al PIB de Canadá.
Fuente: Elaboración propia a partir de datos obtenidos del IFS.

Por otra parte, el efecto de la Bolsa de Valores de Estados Unidos, como se advierte en la figura 5, es nulo en el primer periodo, incluso durante los siete periodos subsecuentes va acumulando sus efectos hasta añadir 0,03 al cabo de 10 periodos.

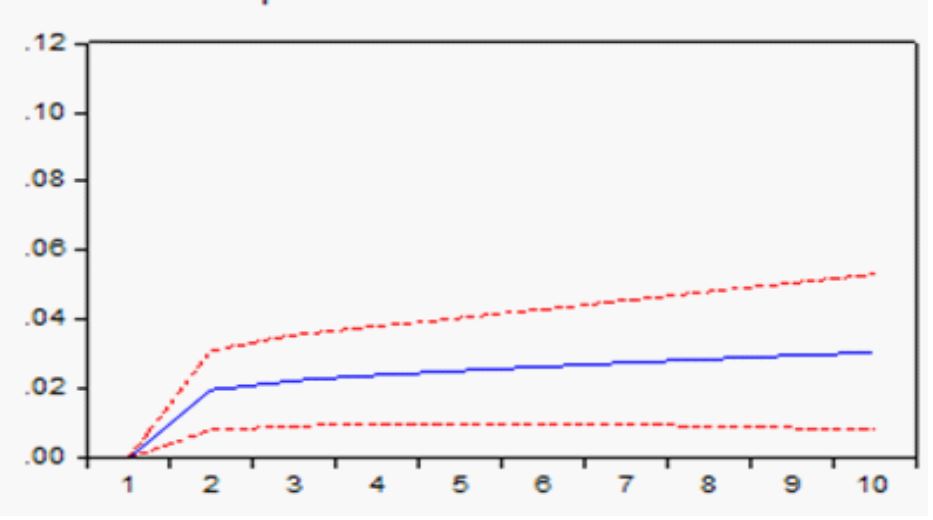
Figura 5
Respuesta a impulso de la Bolsa de Canadá a la bolsa de Estados Unidos.
Fuente: Elaboración propia a partir de datos obtenidos del IFS.

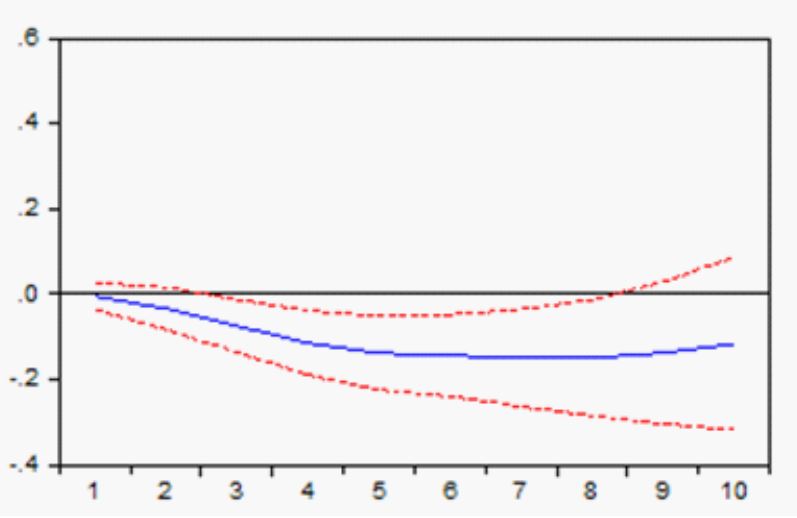
Figura 6
Respuesta a impulso de la Bolsa de México al PIB de México.
Fuente: Elaboración propia a partir de datos obtenidos del IFS.

En el caso del mercado accionario mexicano, el efecto del PIB sobre este es mínimo (0,000123) en el primer periodo e incluso negativo durante los 10 periodos subsecuentes, como aparece en la figura 6.

En tanto que para el caso de M3, en la figura 7 se puede notar un incremento equivalente a 0,029595 en el periodo inicial aumentando a 0,080696 después de 5 periodos. A partir del sexto periodo los efectos tienden a decrecer lentamente hasta convertirse en negativos en el periodo 10.

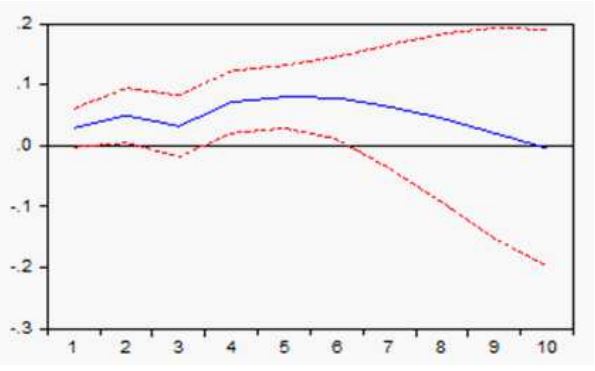
Figura 7
Respuesta a impulso de la Bolsa de México a M3 de México.
Fuente: Elaboración propia a partir de datos obtenidos del IFS.

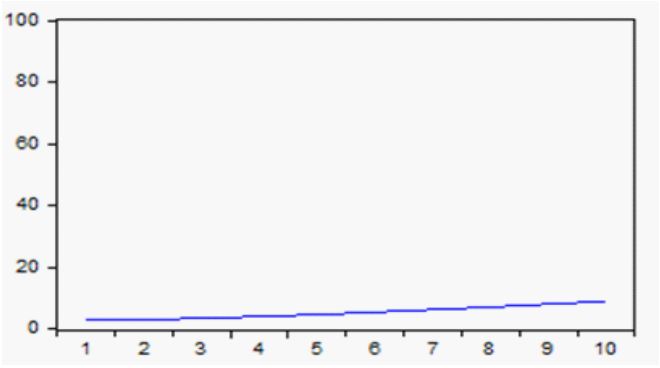
Figura 8
Proporción de la varianza de la Bolsa de Canadá correspondiente al PIB de Canadá.
Fuente: Elaboración propia a partir de datos obtenidos del IFS.

En concordancia con los resultados de las funciones de respuesta a impulsos obtenidos, a continuación se incluye la descomposición de la varianza de cada par de variables. Esto mide la proporción de la variación de cada variable que es generada por shocks en cada variable.

En la figura 8 se muestra como menos del 19% de la varianza de la Bolsa de Canadá corresponde a shocks en el PIB de ese país.

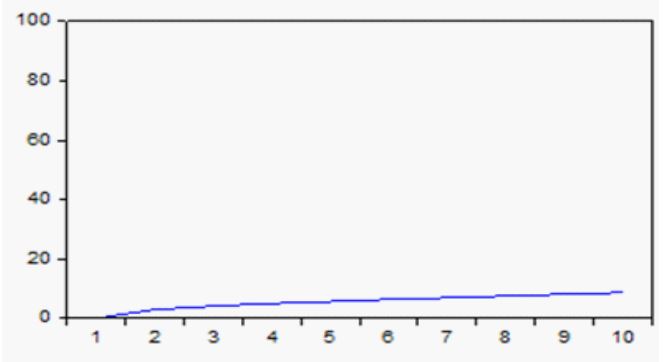
Figura 9
Proporción de la varianza de la Bolsa de Canadá correspondiente a la Bolsa de Estados Unidos.
Fuente: Elaboración propia a partir de datos obtenidos del IFS.

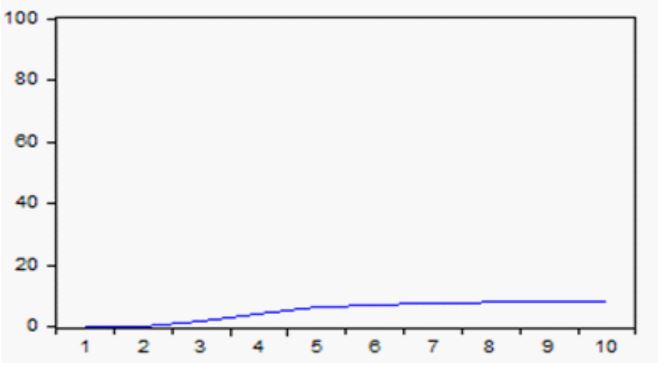
Figura 10
Proporción de la varianza de la Bolsa de México correspondiente al PIB de México.
Fuente: Elaboración propia a partir de datos obtenidos del IFS.

En la figura 9 se aprecia cómo menos del 9% de la varianza de la Bolsa de Canadá corresponde a shocks en la Bolsa de Estados Unidos.

En el caso de la Bolsa mexicana, se observa en la figura 10 que menos del 9% de la varianza corresponde a shocks en el PIB de México.

Por último, en la figura 11 se aprecia como menos del 30% de la varianza de la bolsa mexicana corresponde a shocks en la M3 de México.

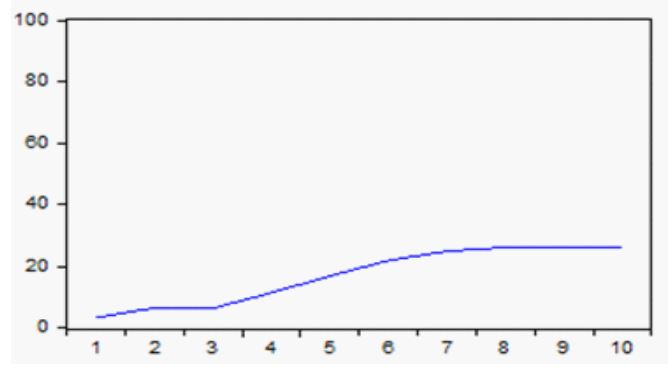
Figura 11
Proporción de la varianza de la Bolsa de México correspondiente a M3 de México.
Fuente: Elaboración propia a partir de datos obtenidos del IFS.

5. Conclusiones

Concerniente a las dos hipótesis planteadas en este trabajo, bajo las cuales se buscó evidencia empírica sobre: a) si el sector económico causa el desarrollo del sector financiero de cada país miembro del área del TLCAN y b) si el sector económico de Estados Unidos causa el desarrollo financiero de cualquiera de los otros países miembros del área del TLCAN; se planteó el objetivo del trabajo para demostrar la causalidad entre el desarrollo del sector financiero y el crecimiento económico para los países de América del Norte: Canadá, Estados Unidos y México. Determinando, en primera instancia, la existencia en estos mercados de una relación entre su sector financiero y las variables de la economía real.

Siguiendo las recomendaciones de Goldsmith (1969) se recuperaron resultados previamente obtenidos referentes a la estacionariedad de las series bajo la prueba ADF. Posteriormente y como lo sugieren Jung (1986), Demetriades y Hussein (1996), Giles (2013), entre otros, se aplicaron contrastes para identificar la posible dirección de la causalidad entre las variables, siendo a través de un análisis de causalidad en el sentido de Granger (1969) y las pruebas econométricas extendidas desarrolladas por Toda y Yamamoto (1995).

Los resultados obtenidos acerca del desarrollo financiero y el crecimiento económico en los tres países de América del Norte mostraron evidencia sobre la direccionalidad de la causalidad entre ellos, que será descrita a continuación. Para el caso del mercado accionario estadounidense, con base en estas pruebas, se puede afirmar que la dinámica de la economía local y de los otros dos países no causa, en el sentido de Granger, a la dinámica financiera norteamericana. En tanto que para Canadá, se encontró evidencia de que la economía de ese país, medida por el PIB, causa en el sentido de Granger al mercado accionario canadiense. También los resultados obtenidos para este país, pusieron de manifiesto la nula influencia que tiene este mercado proveniente de la dinámica económica y financiera de los otros países objeto de estudio. De igual forma, se comprobó que el crecimiento económico de México, medido a partir del PIB y M3, causa en el sentido de Granger al mercado bursátil de este país. El desarrollo financiero mexicano no tiene influencia del crecimiento económico presentado en los otros dos países del bloque comercial.

Así, se afirma que al estudiar de manera conjunta a los tres países, es decir, como un bloque en el cual se interrelacionan los sectores financieros y las economías de los tres países, los resultados obtenidos para este análisis demostraron la nula relación causal que tienen entre sí estos mercados y las economías de los países objeto de estudio. Esto desafía exploraciones empíricas formales desarrolladas en los últimos años, como el trabajo de Hurlin y Venety (2008).

Es obligación comentar que la relación positiva entre el crecimiento económico y el desarrollo de los mercados accionarios de Canadá y México, resultantes en este trabajo, está sujeta al análisis y control de otras variables de la economía real como: el tipo de cambio, la inflación, la inversión extranjera directa, entre otras.

Por otra parte, se observó que la literatura desplegada en el sector financiero respecto a la relación entre crecimiento económico y el desarrollo de los mercados accionarios ha considerado resultados de estacionariedad obtenidos con pruebas de baja potencia como la ADF, para posteriormente buscar una relación causal a través de la metodología desarrollada por Granger (1969). Dicha metodología implica la validación de la cointegración a través de un modelo VAR y requiere de series de tiempo con el mismo orden de integración I(1), situación contraria a los datos mostrados en este trabajo. De esta manera, en la presente investigación se determinó la utilidad de buscar la dirección causal entre variables económicas y financieras con la metodología TY, que incorporó series de diferente orden de integración, I(1) e I(0), y no requirió pruebas preliminares de cointegración.

Referencias

Calderón, César y Liu, Lin (2003). “The direction of causality between financial development and economic growth.” Journal of Development Economics, 72, 1, 321–334. DOI: 10.1016/S0304-3878(03)00079-8.

Cermeño, Rodolfo; Roa, María J. y González, Claudio (2006). “Desarrollo financiero y volatilidad del crecimiento económico: Evidencia para México y Estados Unidos.” Documentos de Trabajo del CIDE, 377.

Diebold, Francis (1998). “The Past, Present, and Future of Macroeconomic Forecasting.” Journal of Economic Perspectives, American Economic Association, 12(2), 175-192. DOI: 10.1257/ jep.12.2.175.

Diebold, Francis (1999). Elementos de Pronósticos, México: Thomson, 330 pp.

Engle, Robert y Granger, Clive W. J. (1987). “Co-integration and error correction: representation, estimation, and testing.” Econometrica, 55, 2, 251-276. DOI: 10.2307/1913236.

Garza, Jesús G. y Vera María E. (2010). “Who Influences Latin American Stock Market Returns? China versus USA”. Centre for Global Finance Working Paper Series. 05/10.

Gilles, Dave (2011, 29 de abril). “Testing for Granger Causality”. (Mensaje 4) Mensaje dirigido a http://davegiles.blogspot.ca/2011/04/testing-for-granger-causality.html.

Gopinath, Munisamy; Kennedy, P. Lynn and Roe, Terry. L. (1995). “Trade, growth, and welfare linkages in North America: An empirical analysis.” The North American Journal of Economics and Finance. 6, 2, pp. 189–201. DOI: 10.1016/1062-9408(95)90016-0.

Granger, Clive W. J. (1969). “Investigation causal relation by econometric models and crossspectral methods.” Econometrica, 37, 3, pp. 425-438. DOI: 10.2307/1912791.

Granger, Clive W. J. (1988). “Some recent developments in a concept of causality.” Journal of Econometrics, 39, pp. 199-211. DOI: 10.1016/0304-4076(88)90045-0.

Gries, Thomas; Kraft, Manfred y Meierrieks, Daniel (2008). “Financial Deepening, Trade Openness and Economic Growth in Latin America and the Caribbean.” Center for International Economics. Working Paper Series. pp. 2008-10. DOI: 10.1080/00036846.2010.498352.

Guisán, M. Carmen (2002). “Causalidad y cointegración en modelos econométricos: Aplicaciones a los países de la OCDE y limitaciones de los test de cointegración.” Working Paper Series Economic Development, 61, pp. 1-47.

Guzmán, María de la P.; Leyva, Soraya y Cárdenas, Almagro (2007). “La relación de causalidad entre el índice bursátil mexicano y el tipo de cambio spot.” Análisis Económico, 51, XXII, pp. 81-105.

Hassana, M. Kabir; Sánchez, Benito y Yuc, Jung-Suk (2011). “Financial development and economic growth: New evidence from panel data.” The Quarterly Review of Economics and Finance, 51, 1, pp. 88–104. DOI: 10.1016/j.qref.2010.09.001.

Hernández, Norma A. y Robins, Russell (2000). “The Relationships between Mexican Stock Market Returns and Real, Monetary and Economic Variables.” Manuscrito.

Hurlin, Christophe y Venet, Baptiste (2008). “Financial Development and Growth: A Re-Examination using a Panel Granger Causality Test.” Hyper Articles en Ligne: halshs-00319995, versión 1. Consultado el 18/04/2014. Disponible [on line]: http://hal.archives-ouvertes.fr/halshs-00319995/

Levine, Ross (1997). “Financial Development and Economic Growth: Views and Agenda.” Journal of Economic Literature, 35, pp. 688- 726 DOI: 10.1596/1813-9450-1678.

Levine, Ross (2004). “Finance and growth: Theory and evidence.” NBER Working Paper Series, num. 10766. DOI: 10.3386/w10766.

Lin, Jin-Lung (2008). “Notes on Testing Causality.” Department of Economics,NationalChengchiUniversity.Consultadoel12/03/2014. Disponible [on line]: http://faculty.ndhu.edu.tw/~jlin/files/causality.pdf

López, Francisco y Rodríguez, Domingo (2010). “¿El desarrollo del mercado accionario genera crecimiento económico en México? Un análisis de series de tiempo.” Economía: Teoría y Práctica. Nueva Época, 32, pp. 33-54.

Lütkepohl, Helmut (2006). New Introduction to Multiple Time Series Analysis. Berlín: Springer, 747 pp. DOI: 10.1080/07474930903472868.

Montero, Roberto (2013). “Test de Causalidad.” Documentos de Trabajo en Economía Aplicada. Universidad de Granada. España.

Muñoz, Evelyn y Vindas, Katia (1995). “Pruebas Extendidas de Granger.” Banco Central de Costa Rica. División Económica. Departamento de Investigaciones Económicas. DIE-NT-04-95. Consultado el 13/06/2014. Disponible [on line]: http://www.bccr.fi.cr/investigacioneseconomicas/metodoscuantitativos/Pruebas_extendidas_de_GRANGER.pdf

Ortiz, Edgar; Cabello, Alejandra y De Jesús, Raúl (2007). “The Role of Mexico’s Stock Exchange in Economic Growth.” The Journal of Economic Asymmetries. 4, 2, 1-26. DOI: 10.1016/j.jeca.2007.02.001.

Oxley, Les y Greasley, David (1998). “Vector autoregression, cointegration and causality: testing for causes of the British industrial revolution.” Applied Economics Journal, 30(10), pp. 387-1397. DOI: 10.1080/000368498325002.

Pagano, Marco (1993). “Financial Markets and Growth. An Overview.” European Economic Review, 37, pp. 613-622 DOI: 10.1016/0014- 2921(93)90051-B.

Pindyck, Robert S. y Rubinfeld, Daniel L. (2001). Econometría: Modelos y Pronósticos. México: McGraw Hill, 661 pp.

Pollack, Molly y García, Álvaro (2004). “Crecimiento, competitividad y equidad: rol del sector financiero.” CEPAL - SERIE Financiamiento del desarrollo, 147.

Schumpeter, Joseph A. (1912). Theorie der Wirtschaftlichen Entwicklung. Leipzig: Dunker & Humblot, The Theory of Economic Development, traducción de R. Opie. Cambridge, MA: Harvard University Press.

Toda, Hiro Y. y Yamamoto, Taku (1995). “Statistical inferences in vector autoregressions with possibly integrated processes.” Journal of Econometrics, 66, pp. 225-250. DOI: 10.1016/0304- 4076(94)01616-8.

Velázquez Orihuela, Daniel y Hernández Veleros, Zeus Salvador (2013). “Una Revisión del Papel del Sistema Financiero en el Crecimiento Económico”. En Temas Selectos de Economía II, 1st ed., pp. 169-179. Pachuca, Hidalgo: UAEH.

Villegas, J. Eddie César (2012). “La Relación de Causalidad entre el crecimiento económico de México y la Inversión Extranjera Directa (IED): Un Modelo de Granger.” Revista Electrónica de Divulgación de la Investigación, 4, pp. 1-32.

Zavaleta, Osmar H. y Urbina, Héctor A. (2011). “Mercados financieros y desarrollo económico: un análisis sobre México.” Ideas CONCYTEG, 6, 68, pp. 226-235.

Zuñiga, Norberto (1992). “Cointegración y corrección de errores en el análisis de las tasas de interés durante el periodo de liberalización financiera.” Financial Services Project. Occasional Paper. 17, (1), Ohio State University, pp. 1-42.

Notas