El gusto por las ciencias abstractas en general, y sobre todo por los misterios de los números, es tremendamente inusual, lo cual no me sorprende porque los seductores encantos de esta sublime ciencia se manifiestan tan sólo a aquellos que poseen el valor para ahondarla en profundidad. Sin embargo, cuando una persona, según nuestras costumbres y prejuicios, se ve obligada a tropezar con muchísimas más dificultades que un hombre, por pertenecer al sexo contrario, a la hora de familiarizarse con estos estudios espinosos y, a pesar de todo, consigue vencer los obstáculos y penetrar hasta sus rincones más oscuros, entonces esa mujer goza sin duda del ánimo más noble, de todo un talento extraordinario y de un genio superior.

Carl Friedrich Gauss¹

introducción

El quehacer científico de las mujeres en las matemáticas generó resultados notables en la disciplina. Para llegar a ello, lo trascendental fue su lucha y las estrategias desarrolladas para concretar la pasión de su vida. Este texto muestra algunas aportaciones en dicho campo por parte de mujeres matemáticas, a lo largo de la historia occidental, en un contexto de violencia estructural, cultural y física. Se realiza una revisión bibliográfica en la que se muestra, por un lado, parte del legado matemático, como la solución de un sistema de ecuaciones con álgebra diofantina, propuesta por Hipatia de Alejandría; la construcción de los números primos de Sophie Germain y el enunciado del teorema de Kovalevskaya. Por otro, se describen las condiciones de violencia estructural en las que desarrollaron su quehacer científico. El objetivo, además del desarrollo matemático expuesto, es el de dilucidar las razones que las llevaron a invertir su energía con el fin de superar tantos obstáculos.

violencia estructural/cultural

En efecto, las mujeres matemáticas enfrentaron violencia estructural/cultural, pues hasta antes del siglo XIX, la educación formal era sólo para los hombres. Muchas de ellas intentaron combatir tal situación, el esfuerzo que hicieron fue mal visto por la sociedad, y ello las condujo al olvido durante muchos años. John Rawls² sostiene que una estructura social justa existe cuando hay una “posición de igual ciudadanía. Esta posición se define por los derechos y libertades que exigen el principio de igual libertad y el principio de la justa igualdad de oportunidades. Cuando los dos principios se satisfacen, todos son ciudadanos iguales y, por tanto, todos ocupan esta posición”.³ Sin embargo, la estructura social ha sido jerárquica y ello no ha dado igualdad de oportunidades, de modo tal que la estructura social deviene en estructura violenta. La violencia estructural⁴ está referida al proceso histórico, y es tan profunda que los sujetos no se percatan de ella. Esta violencia es la base para que existan otros tipos de violencia: la directa y la cultural. Johan Galtung dice:

Una estructura violenta no sólo deja huellas en el cuerpo humano, sino también en la mente y el espíritu. Las cuatro expresiones siguientes pueden considerarse partes de la explotación o refuerzos de los componentes de la estructura. Funcionan impidiendo la formación y movilización conscientes, dos condiciones necesarias para la lucha eficaz contra la explotación.⁵

La violencia estructural coincide con la malnutrición, la marginación y la fragmentación. Por principio, desde el punto de vista de Galtung, hay dos tipos de sujetos creados en el mundo occidental: los elegidos y los no elegidos.

En el mundo “occidental duro” que se vive de manera dicotómica, se encuentra el Yo frente al Otro, el Yo es el elegido por Dios y el Otro es el que pertenece a Satanás. Dios elige a la especie humana, Hombres, Su pueblo, Raza blanca, Clases altas. Satanás selecciona a los animales, plantas, naturaleza, mujeres, los otros, los pueblos de otras etnias, clases bajas, herejes y paganas con estas consecuencias: ecocidio, sexismo, quema de brujas, nacionalismos, imperialismo, racismo, colonialismo, clasismo, explotación, inquisición.

Algunas formas de violencia expresadas por medio de la invisibilización en el campo de la ciencia se pueden constatar por la fama de algunas de ellas, consecuencia de la actividad de sus esposos más que de sus propios trabajos. Ejemplo de ello fue Theon⁶ (572-497 a.C.), más conocida por ser la esposa de Pitágoras, que por su legado acerca de la región áurea. Lo mismo sucedió en Francia 23 siglos después, con la marquesa Émile Du Châtelet (1706-1749), mejor conocida por su relación con Voltaire.⁷

Hipatia de Alejandría (355 o 370-415) sufrió violencia física. Aunque su padre Teón la apoyaba, pagó con su vida⁸ el hecho de ser una mujer independiente y respetada por las élites, a las que educaba en ciencias; pero fue asesinada por algunos cristianos que rechazaron el pensamiento laico.

pensamiento estratégico

Ante esta violencia estructural, las mujeres matemáticas desarrollaron el pensamiento estratégico; por ejemplo, Germain usó un nombre masculino para poder estudiar, pues no podía inscribirse en la universidad. Otras formularon lo que hoy serían consignas del movimiento feminista, como lo hizo la marquesa Du Châtelet, como consecuencia del trato recibido al final de su relación con Voltaire.

La francesa Sophie Germain (1776-1831)⁹ se vio en la necesidad estratégica de firmar sus documentos científicos con el seudónimo de señor Le Blanc; para ser considerados por sus pares científicos. Mary Katherine Johnson (1918),¹⁰ Dorothy Vaughan (1910-2008) y Mary Jackson (1921-2005) (todas ellas de raza afroestadounidese, por lo que recibieron doble discriminación), ante la negativa institucional para desarrollarse en su campo, aprovecharon la oportunidad para estudiar el lenguaje de programación computacional Fortran, como respuesta a la inacción de sus compañeros blancos para el avance de esta tecnología, de tal forma que sólo mediante esta acción estratégica obtuvieron reconocimiento.

la estructura familiar, año 400 a.c.

La familia es considerada como la primera institución que puede, o no, ofrecer condiciones que generen un ambiente propicio para el estudio y el desarrollo humano. Tal ambiente familiar está inmerso en las estructuras históricas, sociales, culturales y políticas de una época determinada.

Para Durant, desde la era platónica, alrededor del año 387 a.C., la institución familiar fue robusta y permaneció hasta mediados del siglo XX (salvo por los esclavos).¹¹ Esta entidad se constituyó históricamente por el padre, la madre, a veces por una segunda esposa; hijas solteras, hijos, esclavos y las esposas e hijos de los esclavos. El poder del padre era decisivo en la dinámica familiar ya que podía disponer del trabajo de sus hijos y dar a sus hijas solteras en matrimonio, en ambos casos como si fueran de su propiedad. Bajo una visión sociológica contemporánea, las dinámicas familiares se han modificado en la actualidad. La estructura familiar se ha disuelto en esa configuración tradicional, de tal suerte que resulta una realidad común la falta del padre, el divorcio y las nuevas configuraciones familiares donde existen familias monoparentales, o matrimonios igualitarios; sin embargo, la función parental patriarcal permanece dentro de las dinámicas familiares, sobre todo en función de la toma de decisiones y la dinámica, así como de la relación de poder que aún permanecen a manera de trasferencia.

En la época clásica la educación era privada, no había escuelas ni universidades públicas. Platón abogó por la educación pública. Los maestros creaban sus propias escuelas, a las que enviaban a los niños a la edad de seis años, concebían al pedagogo como el esclavo que conducía al niño diariamente a la escuela y lo acompañaba en la realización de sus tareas. La educación de las niñas se practicaba en el hogar y se limitaba a las actividades domésticas. Platón proponía que la mujer debía participar en la vida social y no sólo estar destinada a parir, criar hijos y administrar la casa, aun cuando reconocía la diferencia física entre el hombre y la mujer.¹²

la concepción de la mujer

Para el historiador griego Heródoto, la mujer estaba en todas partes; mientras que, para Tucídides, la mujer era invisible y afirmaba que “una mujer decente, como persona, debe ser encerrada en la casa”.¹³ En lo educativo, las madres enseñaban a sus hijas a leer, escribir, contar, hilar, tejer, bordar, bailar, cantar y tocar instrumentos musicales. Platón estableció el principio de la igualdad de oportunidades para ambos sexos, y no sólo lo predicó, sino que lo practicó, reconoció diferencias naturales entre ambos sexos; impartió a sus alumnas una formación considerable en filosofía y literatura. Como resume Reck:

Para decirlo con otras palabras, desde una perspectiva de género, Platón, aunque intenta ofrecer a las mujeres la posibilidad de que se equiparen con los hombres a través del acceso a la educación y que desarrollen una tarea política pública, no pudo escapar al sexismo de su época.¹⁴

esbozo biográfico

Hipatia de Alejandría (355 o 370-415) hija de Teón, profesor de la Universidad de Alejandría, “estaba obsesionada con las matemáticas y con el método de la demostración lógica”, dice Singh.¹⁵ “En un momento en que las mujeres tenían pocas opciones y eran tratadas como propiedad, Hipatia se movía libre e inconscientemente a través de los dominios masculinos tradicionales”, según Sagan, quien la considera símbolo del aprendizaje y de la ciencia.¹⁶ Estudió filosofía, astronomía y matemáticas en Atenas, antes de encabezar la escuela neoplatónica en Alejandría. Por lo que respecta a las matemáticas, es conocida por su trabajo sobre el tratado de Apolonio, referente a las secciones cónicas; según Castro, “[...] sus trabajos más extensos se centraron en el álgebra. Estudió y escribió sobre la aritmética de Diofanto y aportó nuevos desarrollos como las soluciones enteras en el sistema de ecuaciones”.¹⁷ Su trágica muerte, a manos de una turba de cristianos alentada por Cirilo, obispo de Alejandría, “marcó en muchos sentidos el fin de siglos de progreso griego en matemáticas”.¹⁸

El paganismo de Hipatia, que nunca negó sus ideales, queda patente con la frase: “Todas las religiones formales son falaces y no deben aceptarse por respeto a uno mismo”. Donde ataca frontalmente a las religiones y considera inaceptable que se utilicen para gobernar: “Gobernar encadenando la mente por miedo o por temor al castigo en otro mundo es igual de básico como usar la fuerza”. Advierte que “enseñar supersticiones como si fuesen verdades, es terrible. La mente del niño las acepta y cree, y sólo con un gran dolor, y tal vez la tragedia, se podrá librar de ellas con los años”. El pensamiento racional y científico de Hipatia está expresado de la siguiente manera: “Defiende tu derecho a pensar, porque incluso pensar de manera errónea es mejor que no pensar”. Y afirma: “La verdad no cambia porque sea o no sea creída por la mayoría de las personas”.

el legado matemático de hipatia

Hipatia comentó las grandes obras de la matemática griega como las cónicas de Apolonio, que deben su nombre a su obtención mediante diferentes secciones de un cono circular recto (Figura 1).

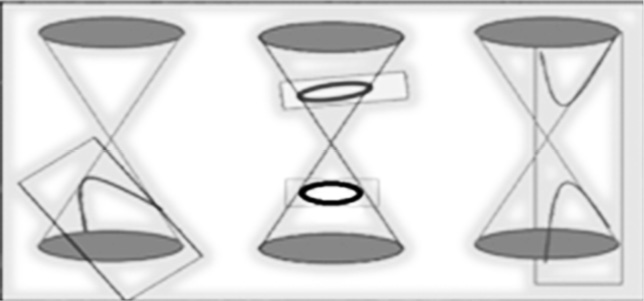
Figura 1
Figura 1
elaboración propia.

En los comentarios de Hipatia sobre la Aritmética de Diofanto se encontró el problema de determinar los cuatro valores enteros del sistema de ecuaciones:¹⁹

x – y = a

x² – y² = (x-y) +b

Para determinar los cuatro valores enteros del sistema procedemos a:

x = a + y

(a+ y)²-y² = a +b

De donde:

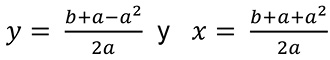
Para que las soluciones x y y sean enteras se debe cumplir que:

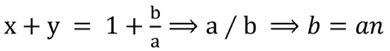
Entonces las soluciones

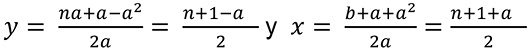
Si a es par entonces a + 1 es impar y 1 – a es impar por lo que n es impar

Si a es impar entonces a + 1 es par y 1 – a es par por lo que n es par

Ejemplo: Sea a = 141 (se debe elegir un n par); sea n = 16, implica que b = 2256 entonces el sistema:

222ª222ªx – y = 141

x² – y² = 141 + 2256

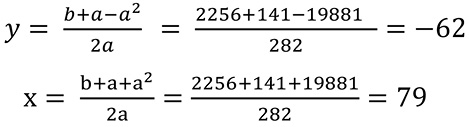
En efecto, se comprueba

79 – (–62) = 141

6241 – 3844 = 141 + 2256 = 2397

El resultado de estos trabajos presentados por Hipatia demostraron la solución entera de un sistema de ecuaciones, lo cual significó un avance en la ciencia interrumpido por su trágica muerte.

La mujer y la Ilustración

En Europa, particularmente en Francia, se produjo un avance significativo durante la época de la Ilustración, donde se sucedieron acontecimientos científicos remarcables en dicho ámbito y en particular en las matemáticas. La reunión entre filósofos y matemáticos relevantes como Newton, Leibniz, Voltaire y J.J Rousseau, entre otros, produjo un movimiento para terminar con el control eclesiástico sobre la educación. En el ámbito político, Francia estaba dividida entre nobleza,²⁰ clero y los financieros, banqueros y el resto de la población. Hay que decir que las mujeres de las que hablaremos son parte de la nobleza de ese tiempo, de familias con recursos, lo que indica que para crear e investigar, es condición necesaria, aunque no suficiente, contar con condiciones económicas mínimas.

La mujer, no obstante su pertenencia a la clase privilegiada, en cuanto a las oportunidades de educación de nivel científico, éstas no cambiaron significativamente desde la era de Platón. J.J Rousseau en su obra Emilio o De la educación,²¹ crea el personaje de Sofía, la esposa de Emilio, cuya educación es inferior a la de él, una mera preparación para el matrimonio, retomando las ideas del obispo Fenelón en el siglo XVII,²² quien sostuvo que la educación a la mujer debía ser inferior a la del hombre, porque no sólo necesitaba saber menos, sino que era menos competente.

Durante la Ilustración, sin embargo, se desarrolló una ambivalencia: por un lado, el discurso de los derechos naturales colocó a la mujer en posibilidades de comenzar a trazar visos de emancipación, los cuales finalmente cristalizarían en la Declaración de los derechos de la mujer y la ciudadana, realizada por Olimpia de Gouges, mientras que, al mismo tiempo, la cultura falocéntrica continuaba dominando: la Enciclopedia consignaba una idea tal de las mujeres que dependía de visiones negativas del Renacimiento y las consideraciones de la diferencia, con base en el orden biológico, pretendían dar identidad a la mujer desde posturas pseudomédicas y filosóficas.²³

En opinión de Singh, “Francia adoptó la actitud más discriminatoria hacia la mujer culta declarando que las matemáticas son inadecuadas para las mujeres y van más allá de su capacidad mental”.²⁴

Émile Du Châtelet fue hija del barón de Breteuil, un diplomático culto que la educó esmeradamente. Marquesa de Châtelet por su matrimonio con un militar tolerante, fue amiga de personalidades de la época y amante de Voltaire. El talento y curiosidad de Du Châtelet la llevaron a interesarse por todas las manifestaciones artísticas, a traducir obras clásicas y a escribir ensayos de divulgación científica.²⁵ Las condiciones de privilegio cultural y económico y su relación, si bien amorosa, también como colega con Voltaire, le permitió estudiar las difíciles obras de Leibniz y Newton; y aunque tuvo participación en el libro Elementos de la filosofía de Newton, únicamente se publicó con la autoría de Voltaire; el nombre de Du Châtelet sólo aparece en una carta de reconocimiento del escritor francés.

En la época de Luis XV las opiniones científicas de una mujer, como las de la Marquesa Émilie, generaron envidia y tuvo que soportar el desprecio y silencio público. Por ello, en su Discurso sobre la felicidad reivindicó el derecho a la educación de las mujeres como el camino para su reconocimiento social:

Si yo fuera el rey, reformaría un abuso que condena por así decirlo a la mitad del género humano [...] Haría participar a las mujeres en todos los derechos de la humanidad y sobre todo en los del intelecto [...] Estoy persuadida de que muchas mujeres o ignoran sus talentos, por el vicio de su educación, o los esconden por prejuicio y falta de coraje en su espíritu.²⁶

Por lo que: “Cuanto menos depende nuestra felicidad de los demás, más fácil nos resulta ser felices [...] el amor al estudio es de todas las pasiones la que más contribuye a nuestra felicidad”.²⁷

Por su parte, el carácter de María Gaetana Agnesi (1718-1799) fue diame-tralmente opuesto al de su contemporánea, la Marquesa Du Châtelet. Ella deseaba una vida religiosa, pero por satisfacer a su padre continuó con sus estudios. Nació en una familia numerosa, pero con los medios suficientes. Un tutor privado estimuló a Agnesi para que se dedicara al estudio del cálculo diferencial. Fue una niña prodigio, y en su adolescencia “acudían intelectuales, tanto italianos como extranjeros, para oír las disertaciones de María sobre temas matemáticos, filosóficos y científicos”.²⁸ A los 30 años publicó Instituzione Analitiche, “libro de texto para estudiar el cálculo diferencial e integral, en el que aparecían las series infinitas y las ecuaciones diferenciales”,²⁹ obra que fue aclamada por los científicos de la época, traducida a diversos idiomas y usada como libro de texto. Destacó, además, por su análisis detallado y didáctico de la curva sinusoide o senoide, conocida por ello como curva de Agnesi.³⁰ No obstante su capacidad, la Academia de Ciencias de París se negó a aceptarla como miembro. Durante el periodo intermedio entre el nombramiento de Agnesi en la cátedra de Bolonia en 1750 y el triunfo de Phillipa Fawcett (1868-1948) en el examen matemático Tripos³¹ de Cambridge en 1890, las mujeres no recibían grados formales. De ahí que un conjunto de mujeres sobresalientes que hicieron avances pioneros en el campo de las matemáticas provenientes de China, Rusia, Francia, Alemania y Estados Unidos, formaron la coalición STEM (por sus siglas en inglés, ciencia, tecnología, ingeniería y matemáticas) y así allanaron un poco el camino para muchas mujeres.³² Al final de su vida, Agnesi se recluyó en un convento para satisfacer su pasión religiosa, aislándose de los matemáticos de la época.

Sophie Germain (1776-1831) nació en Francia, en el seno de una familia burguesa. En principio, sus parientes se opusieron tajantemente a su estudio e interés por las matemáticas; según cuenta la historia, Germain se dispuso a aprender por su cuenta las bases de la teoría de números y del cálculo, estudiando hasta la madrugada. Enterado su padre, decomisó velas y ropa abrigada, y eliminó la calefacción, por lo que la joven tuvo que esconder algunas velas y taparse con cobijas para continuar sus estudios. Al cabo de un tiempo, el padre transigió.³³ Sin ayuda de tutor alguno, se acercó a estudiantes de la Escuela Politécnica, quienes le facilitaron sus apuntes de clase y bajo el nombre supuesto de M. Le Blanc, un antiguo alumno de ésta, envió un ensayo sobre análisis matemático al profesor Joseph-Louis Lagrange, quien sorprendido buscó al autor y enterado de la identidad de Germain, la aceptó como alumna a pesar de su género. Colaboró con Adrien-Marie Legendre y mantuvo correspondencia con Carl Friedrich Gauss;³⁴ ganó un concurso de la Academia Francesa de Ciencias –fue la primera mujer en conseguirlo–, lo que le granjeó el privilegio de asistir a las sesiones académicas. Trabajó en el teorema de Fermat que, a decir de Singh, “constituyó su mayor aportación a las matemáticas”,³⁵ contribuyendo a su eventual solución tres y medio siglos después. Un ejemplo del legado de Germain, que como muchos matemáticos intentaron demostrar, es la conjetura de Fermat (1637), que plantea:

Es imposible escribir un cubo como la suma de dos cubos, o una cuarta potencia como la suma de dos cuartas potencias, y en general para ningún número que sea una potencia mayor que dos ser escrito como la suma de dos potencias del mismo grado.³⁶

Es decir, la ecuación diofantina x^p + y^p = z^ptiene solución entera para grado mayor o igual que tres. Esta conjetura³⁷ atormentó a los mejores matemáticos del mundo durante 350 años y fue demostrada por un trabajo de ocho años de Andrew Wiles.

En efecto, para p = 1 siempre existe solución entera para la ecuación x + y = z.

Para p = 2, es el caso del teorema de Pitágoras a² + b² = c². A las soluciones enteras del teorema se les llama ternas pitagóricas. Por ejemplo (3, 4, 5), (6, 8, 10).

Se le da el nombre de números primos de Sophie de Germain a los números p, donde p es un primo y P = 2 p + 1 también lo es.

Por ejemplo: 2 y 3 son números primos de Sophie de Germain, porque 2(2) + 1 = 5 y 2(3) + 1 = 7; pero el 7 no lo es, ya que: 2(7) + 1 = 15 que ya no es primo.

Los números primos de Sophie menores que 100 son: 2, 3, 5, 11, 23, 29, 41, 53, 83 y 89. Estos números primos son importantes porque Sophie demostró que aunado a ciertas propiedades que deben cumplir P y p, en particular que p no divida a xyz el producto de las tres incógnitas de la ecuación de Fermat es cierto para

n = p.

Mujeres en transición: el siglo XIX

Siglo de guerras, revoluciones y turbulencias, no por ello, o tal vez, por ello mismo, la ciencia no deja de desarrollarse. En el caso de las mujeres todavía persiste la dominación del padre en la familia, tanto en Europa y Estados Unidos aún está prohibida la asistencia de las mujeres a la universidad.

A pesar de esto, las mujeres veían un escenario en transición pues, usadas políticamente en cada revolución, las estructuras las regresaban a los lugares domésticos. Aun así, su papel se multiplica, y en muchos sentidos las industrializaciones las incluyen económicamente en condiciones más desfavorables y sin posibilidades de disfrutar el fruto de su trabajo.³⁸ La educación para mujeres se insinúa, su instrucción no está pensada para el crecimiento personal, pero desde la familia logra espacios de influencia.

Aunque se vislumbra el nacimiento del movimiento feminista, el racismo y la esclavitud del afroamericano persiste en Estados Unidos. El 10 de agosto de 1827 llegó un anónimo firmado con el nombre de Matilde, al primer periódico “negro” donde hace una demanda para la educación femenina y negra. Justamente cuando Emma Hart Willard y Catharine inician un movimiento feminista.³⁹

Sofía Kovalevskaya (1850-1891) provenía de una noble familia rusa y educada; a pesar de que su padre en principio le prohibió tomar clases de matemáticas, a hurtadillas Sofía estudió un libro escrito por un profesor vecino, quien intercedió para que pudiera continuar sus estudios; entonces “la familia al completo se traslada a San Petersburgo [sic], donde Sofía comienza a estudiar [sic] cálculo”;⁴⁰ debido a las costumbres de la época –que no veían con benevolencia que una mujer viajara sola o viviera lejos de su familia– contrajo matrimonio (tuvo una hija)⁴¹ con el objetivo de ingresar a alguna universidad que admitiera mujeres. Acudió primero a la Universidad de Heidelburg y tomó clases sin estar inscrita, y luego a la de Berlín, donde impresionó a Karl Weierstrass –profesor de matemáticas a la altura de Cantor y Frobenius–, quien accedió a darle clases privadas. En 1874 se doctoró con honores en la Universidad de Gotinga; en 1883 ingresó como conferencista a la Universidad de Estocolmo, convirtiéndose al año siguiente en profesora titular, para luego asumir el cargo de editora de la revista Acta Mathematica y después la jefatura del Departamento de Mecánica, convirtiéndose en la primera mujer en conseguir tal honor en una universidad europea; también fue la primera mujer en ser elegida como miembro correspondiente de la Academia Imperial Rusa de Ciencias. Aquejada por la depresión y abatida por la muerte de su esposo y de su hermana, falleció de neumonía en 1891.

Según Castro, Kovalevskaya “no sólo fue una matemática brillante cuyas investigaciones son aplicadas en las matemáticas hasta nuestros días; además fue una firme luchadora de los derechos de las mujeres reivindicando su importancia en el mundo intelectual”.⁴²

Hacia mediados del siglo XIX, en 1842, Cauchy definió lo que se entiende por un problema de Ecuaciones Diferenciales Ordinarias con valores o condiciones iniciales y probó los dos primeros teoremas de existencia y unicidad para la ecuación general de primer orden.

Teorema 1: Si f (x, y) es de clase C¹ en D, dominio en R² y (x₀, y₀) ∈ int D entonces el problema

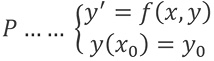
Tiene una única solución ϕ localmente, es decir:

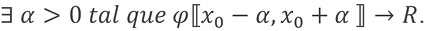
Teorema 2: Si f (x, y) es de clase C¹ en D, dominio en R² y (x₀, y₀) ∈ int D entonces el problema P tiene localmente una única solución analítica.

Weiestrass, como director de tesis de doctorado, le propuso a Kovalevskaya extender este problema a valores iniciales en Ecuaciones Diferenciales Parciales.

Teorema Kovaleskaya:

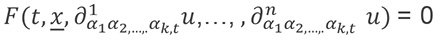
es una ecuación diferencial parcial analítica en todos sus argumentos, con las condiciones iniciales:

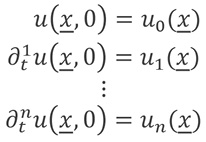
Con uj (x) analíticas en un dominio Ω de R^k entonces, existe una única solución analítica u (t, x) sobre [α, α] × Ω, para α>0.

Para su enunciado y demostración véase I.G. Petrovsky.⁴³

Winifred Edgerton Merrill (1862-1951), estadunidense, comenzó su educación con tutores privados y luego en el colegio femenino Wellesley; solicitó su ingreso en el doctorado en matemáticas y astronomía de la Universidad de Columbia, pero fue rechazada al principio; tras exponer su caso ante las autoridades fue aceptada, aunque se le prohibió tomar clases e interactuar con sus compañeros, por lo que estudió por su cuenta el texto del curso. Fue la primera mujer en obtener un doctorado en matemáticas y la primera en graduarse en la Universidad de Columbia. Participó en la fundación del colegio Barnard en Nueva York, primera institución secular en otorgar grados en artes liberales a las mujeres y fundó también la escuela Oaksmore para mujeres jóvenes.

Emmy Noether (1882-1935) creció en un hogar acomodado en Bavaria y recibió la educación propia de una joven de su condición y de acuerdo con su época (cocinar, atender el hogar, tocar piano). Inicialmente pretendió dedicarse a la enseñanza de idiomas, pero prevaleció su vocación matemática; “de otro modo habríamos perdido a la matemática más importante de la historia, según palabras del propio Einstein”.⁴⁴ Obtuvo permiso para ser oyente en la Universidad de Erlenger, donde uno de sus hermanos era estudiante y su padre profesor de matemáticas;⁴⁵ ahí obtuvo su doctorado con honores. A pesar de tener amplia capacidad para ello, no se le permitió dar clases en esa universidad, aunque se desempeñó como investigadora y auxiliar de su padre. Sus trabajos teóricos fueron empleados con provecho por el propio Albert Einstein, quien declaró que Noether “fue el genio matemático creativo más significativo hasta el momento desde que comenzó la educación superior de las mujeres”.⁴⁶ Con el auxilio de un par de colegas, y gracias al cambio de actitud en la Alemania de la posguerra, en 1919 obtuvo la autorización para enseñar en una universidad alemana; si bien el salario era muy modesto, el hecho de haber recibido una herencia familiar le permitió concentrarse en sus investigaciones y sus alumnos. Además del teorema que lleva su nombre, Noether fue pieza clave en el desarrollo del álgebra abstracta moderna.

El ascenso de los nazis al poder y la posterior expulsión de los profesores judíos de las universidades, obligaron a Noether a huir de Alemania. Según Castro, durante su estancia en Estados Unidos, “tuvo la oportunidad de impartir seminarios en el Instituto de Altos Estudios de Princeton, donde trabajó con Albert Einstein e introdujo elementos algebraicos cruciales utilizados en la teoría de la relatividad”.⁴⁷

Euphemia Haynes (1890-1980) nació en Estados Unidos en el seno de una familia acomodada de raza mixta, teniendo oportunidades impensables para otras familias afroestadounideses. Licenciada en matemáticas y psicología por el colegio Smith, dio clases a nivel primario y secundario en escuelas públicas. Se casó en 1917 y junto con su esposo ingresó en la Universidad de Chicago, donde ella emprendió estudios de posgrado en matemáticas. Obtenida la maestría, estableció y encabezó el Departamento de Matemáticas en el colegio Miner’s Teachers; luego completó el doctorado en matemáticas en la Universidad Católica de América, convirtiéndose en la primera mujer afroestadounidese en obtener dicho grado. Además de la enseñanza, dedicó buena parte de su vida a tratar de mejorar las condiciones de vida de los menos favorecidos y de los estudiantes afroamericanos.

El siglo XX: racismo y lucha

El siglo de la Segunda Guerra Mundial y de los viajes espaciales, entre otros acontecimientos importantes, generó un cambio decisivo en el estatus de la mujer, debido al aumento en el número de mujeres empleadas fuera del hogar. La guerra abrió nuevas vías de empleo, especialmente en la industria, que hasta ahora había sido reservada a los hombres. Sin embargo, como secuelas de la esclavitud y el racismo nunca acabado, tres mujeres estadounidenses empleadas en la NASA como calculadoras para apoyar la logística de los viajes espaciales, trabajan en un contexto de racismo donde el hombre blanco tiene todas las libertades y consideraciones laborales.

Dorothy Vaughan (1910-2008) fue matemática de la Administración Nacional de la Aeronáutica y del Espacio, más conocida como NASA (por sus siglas en inglés) y contribuyó al lanzamiento al espacio de los primeros satélites estadounidenses. Licenciada en matemáticas por la Universidad Wilbeforce en Ohio, la Gran Depresión evitó que prosiguiera con sus estudios de posgrado, y la obligó a dar clases en una secundaria segregada. Contrajo matrimonio y crió a seis hijos. En 1943 fue contratada como matemática por la NACA (antecedente de la NASA); sin embargo, por ser afroestadounidense, tenía que cumplir con las normas segregacionistas aún vigentes. No obstante, logró ascender hasta encabezar el grupo de West Computing en Langley; según Talithia Williams: “Desde esa posición, pudo colaborar con computadoras de otros grupos, hacer recomendaciones de personal y abogar por computadoras femeninas, lo que hizo con entusiasmo, independientemente del color de su piel”.⁴⁸ Finalmente, en 1958 fue abolida la segregación en las instalaciones de la NASA, lo que permitió que Vaughan se integrara al grupo de expertos en la vanguardia de la computación electrónica, haciéndose experta en programación Fortran, contribuyendo al programa del lanzamiento de satélites y calculando la trayectoria de múltiples misiones espaciales, entre ellas la del primer estadounidense en el espacio (Shepard) y la del Apolo 11. A pesar de tales logros, no pudo ascender más en el organigrama de la NASA y se retiró en 1991, pero contribuyó al trabajo de otras destacadas mujeres dentro de la organización, particularmente el de otras mujeres afroestadounidenses.

Katherine G. Johnson (1918) fue responsable de los cálculos de la misión de Shepard al espacio. Desde temprana edad dio muestras de ser un prodigio, así que le permitieron entrar al colegio estatal de Virginia Occidental a los 15 años para estudiar inglés, francés y matemáticas. Uno de sus profesores, reconociendo su talento, creó un curso sobre la geometría analítica del espacio específicamente para ella. Después de graduarse con honores en 1937, dio clases en una escuela pública afroestadounidense; dos años después ingresó a la Universidad de Virginia Occidental tras la decisión del Estado de desegregar las escuelas de posgraduados. Pero Johnson abandonó el programa para casarse y formar una familia. En 1953 se integró al equipo de la NACA, para hacer cálculos matemáticos y analizar información de pruebas de vuelo; sus conocimientos le permitieron formar parte de un equipo masculino de investigación de vuelo y contribuir en diversos proyectos, rompiendo en el proceso con varios tabúes sexistas y racistas. Además de calcular la trayectoria del vuelo de Shepard, contribuyó en los cálculos de otras misiones, notablemente, en la del Apolo 11. Se retiró en 1986 y en 2015 recibió –de manos del presidente Barack Obama– la Medalla Presidencial de la Libertad, el máximo honor otorgado por Estados Unidos a los civiles; Obama consideró que Johnson era “una pionera que rompió las barreras de raza y género y mostró a generaciones de jóvenes que todos pueden sobresalir en matemáticas y ciencias”.⁴⁹

Mary Winston Jackson (1921-2005) fue matemática, ingeniera y maestra. Estudio en el Instituto Hampton, licenciándose en matemáticas y física. Enseñó durante un año matemáticas en una escuela segregada, e ingresó en 1951 a la NACA como una de sus matemáticas investigadoras (conocidas coloquialmente como computadoras).⁵⁰ Se casó y tuvo un hijo.

Ante la oferta de ser ascendida de matemática a ingeniera, Jackson se inscribió en la Universidad de Virginia, pero tuvo que solicitar un permiso especial de la ciudad para asistir a algunas de las clases, puesto que eran impartidas en planteles exclusivos para blancos. En 1958 fue nombrada ingeniera aeroespacial, convirtiéndose en la primera mujer afroestadounidense en lograrlo. No obstante sus múltiples contribuciones y reportes de investigación, no pudo acceder a círculos dominados por hombres, lo que la hizo buscar un cargo administrativo que le permitiera apoyar a sus colegas (mujeres y miembros de minorías); como administradora en Langley del Programa Federal para las Mujeres de la NASA, Jackson “inició muchos cambios [...] destacó los logros de los grupos con poca representación y ayudó a contratar a muchas matemáticas, científicas e ingenieros altamente calificados”.⁵¹

Estas tres científicas afroestadounidenses –Vaughan, Johnson y Jackson– fueron objeto de un merecido homenaje en el libro Hidden Figures de Margot Lee Shetterly, llevado luego a la pantalla grande –en 2016, con el mismo nombre– por Theodore Melfi. Según Castro, Vaughan, Johnson y Jackson “contribuyeron a allanar el camino para el resto de las científicas que vendrían a continuación. Ellas han servido y servirán de referencia para futuras generaciones de mujeres científicas”.⁵²

Maryam Mirzakhani nació en Teherán en 1977 y creció durante la guerra entre Irán e Irak y sus secuelas. Gracias a su hermano adquirió el gusto por las matemáticas. Estudió en una secundaria exclusiva para mujeres y junto con una compañera solicitó y obtuvo la oportunidad de tomar un curso especial de solución de problemas matemáticos, que les permitiría integrarse al equipo olímpico iraní –convirtiéndose en las primeras mujeres en ser aceptadas en el mismo– y competir en las olimpiadas de la disciplina que se celebrarían en Hong Kong en 1994. En esa ocasión, Maryam ganó el oro y su compañera la plata; Mirzakhani repetiría su triunfo el año siguiente en Toronto.

En 1995 Maryam ingresó a la Universidad de Sharif y en 1998 sobrevivió a un trágico accidente en el que perdieron la vida varios jóvenes talentos matemáticos iraníes; un año después entró a Harvard, donde la dirigió Curtis McMullen, ganador de la medalla Fields en 1998. En 2004 obtuvo el doctorado; dice Talithia Williams que con esa investigación Mirzakhani “resolvió dos antiguos problemas sobre el volumen de los espacios de módulos y cómo su medición podría aplicarse a la teoría de cuerdas”.⁵³ Ese mismo año aceptó la beca Clay para investigación y fue nombrada profesora asistente de matemáticas en Princeton; en 2008 se convirtió en profesora de matemáticas en Stanford. En 2005 contrajo matrimonio con un científico checo y seis años después dio a luz a una hija. Su trabajo en colaboración con Alex Eskin, publicado en 2013, fue proclamado como el inicio de una nueva era y los hizo acreedores al premio Satter otorgado por la Sociedad Americana de Matemáticas; al año siguiente se le otorgó la medalla Fields,⁵⁴ convirtiéndose en la primera (y a la fecha, única) mujer ganadora de dicha distinción. En 2015 se integró a la Academia de Ciencias de París y a la Sociedad Filosófica Americana, en 2016 a la Academia Nacional de Ciencias y en 2017 a la Academia Americana de Artes y Ciencias. Lamentablemente en 2013 le diagnosticaron cáncer, sucumbiendo a la enfermedad en julio de 2017. En opinión de Sergio Castro, el legado de Mirzakhani “es muy innovador [...] y sus descubrimientos se pondrán en práctica y tendrán un gran impacto en el futuro del área de sistemas dinámicos”, y agrega que “su obra [...] servirá como fuente de inspiración para muchas científicas y científicos de todo el mundo”.⁵⁵

Siguiendo con la línea del pensamiento estratégico de acuerdo con Michael Suk-Young Chwe,⁵⁶ estas mujeres procuraron subvertir el estatus que ocupa-ban por su género. Ellas diseñaron estrategias, a diferencia de quienes no desarrollan el pensamiento estratégico, porque no lo necesitan; como aquellos cuerpos humanos que han sido racializados cuando se les marca por sus líneas: religiosas, étnicas, culturales, ideológicas, lingüísticas, sexuales y género según Crenshaw,⁵⁷ y Grosfoguel,⁵⁸ con lo cual son racializados como superiores o como inferiores (Fanon).⁵⁹ Los masculinos, heterosexuales, blancos, ricos y occidentales son superiores y pertenecen a la zona del ser; los inferiores habitan en la zona del no-ser y son: las mujeres, los niños y niñas, los homosexuales, lesbianas, trasvestis, transexuales, transgéneros, intersexuales, campesinos/as, obreros/as, artesanos/as.⁶⁰ Los hombres heterosexuales, blancos y ricos al tener una condición social favorable, están acostumbrados a estos entornos sociales bien estructurados para ellos; no tienen la necesidad de desarrollar estrategias para ingresar a las universidades o a los círculos intelectuales, pues esos ambientes son creados por y para sí mismos.

El talento no tiene género. Newton el padre del cálculo, también sufrió y fue desdeñado cuando era joven y tuvo que superar condiciones adversas. Su madre lo matriculó en el college como subsizar, “nombre que se daba a los estudiantes pobres que contribuían a financiar su formación sirviendo como criados a media jornada a otros alumnos cuyos padres les daban completo apoyo”.⁶¹

Las estructuras sociales determinaron que el talento matemático de la mujer permaneciera oculto y obligara a superar tal orden con la fuerza interna de crear estrategias para lograr sus metas; y no sólo en el campo de las matemáticas, sino también en el del arte, específicamente en la escultura que requiere de la ayuda de la geometría. En este caso tenemos a Camille Claudel (1864-1943), escultora apasionada y amante de August Rodin, quien la internó en un manicomio argumentando locura; ella, en el séptimo año de su encerramiento, escribió: “Tras apoderarse de la obra realizada a lo largo de toda mi vida, me obligan a cumplir los años de prisión que tanto merecían ellos”.⁶²

Las mujeres que hicieron descubrimientos matemáticos, evidenciaron que el gozo por realizar sus pasiones fue más fuerte que las adversidades que enfrentaron sólo por el hecho de ser mujer, y estimula pensar qué sucedería si toda esa energía se destinara a la realización de un trabajo placentero, artístico o científico, al no tener que enfrentar adversidades construidas por un mundo injusto; pues la justicia se trata de que haya igualdad, igualdad civil, igualdad entre ricos y pobres, entre hombres y mujeres.

En este sentido, Platón decía que la justicia “es dar a cada cual aquello que se le debe”, también se entiende que la idea de la justicia va ligada a lo bueno y lo malo, pero esto se ve afectado de acuerdo con una persona, con una comunidad y con la etapa histórica en la que se encuentra. Sin embargo, las cosas buenas o malas son así en relación con el placer o con el dolor.⁶³ El placer y el dolor son ejes sobre los que giran las pasiones y, por supuesto, la vida. Una persona hará siempre aquello que le cause placer. Flores Rentería menciona que: “El objeto de deseo, el fin deseado, es aquello que pone en movimiento al pensamiento”.⁶⁴ Con esto se comprende qué es lo que movía a aquellas mujeres, su pasión por el conocimiento, y ahora son parte de la historia de la ciencia.

Referencias

Carta a Sophie Germain, apud Simon Singh, El enigma de Fermat (traducción: David Galadí y Jordi Gutiérrez), México, Planeta, 1999, p. 121.

John Rawls, Teoría de la justicia, México, Fondo de Cultura Económica, 2002.

Graciela Sánchez Guevara e Irene Sánchez Guevara, “Diagnóstico y modelación de la violencia intra-universitaria en la UACM”, en Miradas críticas a la complejidad de la violencia universitaria, México, Editorial Fontamara/UACM-CHyCS/Instituto de Ciencia y Tecnología, Secretaría de Ciencia, Tecnología e Innovación, 2015, p. 30.

Talitha Williams, Power in Numbers. The Rebel Women of Mathematics, Estados Unidos, Race Point, 2018.

Will Durant, The Life of Greece. The Story of Civilization II, op. cit., pp. 306-307.

Werner Wilhelm Jaeger, Paideia. Los ideales de la cultura griega, México, Fondo de Cultura Económica, 1978, pp. 639-640.

Will Durant, The life of Greece. The Story of Civilization II, op. cit., p. 305.

Adela Reck, “Platón: ¿feminista o misógino en República?”, Memoria Académica, II Jornadas del Centro Interdisciplinario de Investigaciones en Género, 28, 29 y 30 de septiembre de 2011, La Plata, Argentina [http://www.memoria.fahce.unlp.edu.ar/trab_eventos/ev.4960/ev.4960.pdf], fecha de consulta: 7 de octubre de 2018.

Simon Singh, El enigma de Fermat, op. cit., p. 113.

Carl Sagan, Cosmos, Nueva York, Random House, 1983, p. 336 (traducción propia).

Sergio Castro, Historia de las matemáticas. Del cero al infinito, Madrid, Galobart, 2018, cap. 19.

Clifford A. Pickover, El libro de las matemáticas (traducción: Miguel Serrano et al.), Madrid, Librero, 2018, p. 78.

Will y Ariel Durant, The Age of Voltaire, The Story of Civilization IX, Estados Unidos, Simon and Schuster, 1966, p. 251.

J.J. Rousseau, Emilio o De la educación, Madrid, Alianza, 2011.

Loise Gottschalk, Loren MacKinney y Earl Pritchard, Historia de la Humanidad, tomo 6, Barcelona, Planeta, 1981, p. 533.

Alicia Puelo (ed.), La Ilustración olvidada, Madrid, Anthropos, 1993, pp. 14-15.

Simon Singh, El enigma de Fermat, op. cit., p. 115.

Fernando Savater, “Reportaje: Aproximaciones Madame Voltaire”, El país. Este artículo apareció en la edición impresa del 16 de diciembre de 2006.

Mujeres que hacen historia [https://mujeresquehacenlahistoria.blogspot.com/2010/01/siglo-xviii-emilie-de-chatelet.html], fecha de consulta: 1 de octubre de 2018.

Sergio Castro, Historia de las matemáticas. Del cero al infinito, op. cit., cap. 58.

Carmen Heredero de Pedro y Esther Muñoz Hernández (coords.), Otras miradas. Aportaciones de las mujeres a las matemáticas [https://www.um.es/igualdad/recursos/2013/Otras_miradas._Aportaciones_de_las_mujeres_a_las_matematicas.pdf], fecha de consulta: 13 de mayo de 2018.

Talithia Williams, Power in Numbers: The Rebel Women of Mathematics, Estados Unidos, Race Point, 2018.

Luis Fernando Areán Álvarez, Fermat. El teorema de Fermat. El problema más difícil del mundo, Argentina, RBA, 2012, p. 18.

José William Porras Ferreira, “Último teorema de Fermat. Una demostración sencilla”, Cartagena, 3 de marzo de 2011 [https://historiaybiografias.com/DEMOSTRACION%20SENCILLA%20TEOREMA%20DE%20FERMAT.pdf], fecha de consulta: 11 de agosto de 2018.

Geneviéve Fraisse y Michelle Perrot, “Introducción”, en George Duby y Michelle Perrot (dirs.), Historia de las mujeres, tomo 4, Madrid, Taurus, p. 7.

Anonymous: On Educating Negro Women, The Annals of America, vol. 5, 1968, Encyclopedia Britannica.

Sergio Castro, Historia de las matemáticas. Del cero al infinito, op. cit., cap. 68.

Sergio Castro, Historia de las matemáticas. Del cero al infinito, op. cit., cap. 68.

I.G. Petrovsky, Lecciones sobre ecuaciones en derivadas parciales, La Habana, Ciencia Técnica, Instituto de libre, 1969, pp. 23 y 45.

Sergio Castro, Historia de las matemáticas. Del cero al infinito, op. cit., cap. 74.

Talithia Williams, Power in Numbers..., op. cit., p. 36 (traducción propia).

Sergio Castro, Historia de las matemáticas. Del cero al infinito, op. cit., cap. 74.

Talitha Williams, Power in Numbers..., op. cit., p. 68 (traducción propia).

Talitha Williams, Power in Numbers..., op. cit., p. 81 (traducción propia).

Sergio Castro, Historia de las matemáticas. Del cero al infinito, op. cit., cap. 87.

Talitha Williams, Power in Numbers..., op. cit., p. 181 (traducción propia).

Sergio Castro, Historia de las matemáticas. Del cero al infinito, op. cit., cap. 99.

Michael Suk-Young Chwe, Jane Austen, Game Theorist, Estados Unidos, Princenton, 2013.

Kimberlé Williams Crenshaw, “Mapping the Margins: Intersectionality, Identity Politics, and Violence Against Women of Color”, en Martha Albertson Fineman, Rixanne Mykitiuk (eds.), The Public Nature of Private Violence, Nueva York, Routledge, 1994, pp. 93-118.

Ramón Grosfoguel, “Decolonizing Post-Colonial Studies and Paradigms of Political-Economy: Transmodernity, Decolonial Thinking and Global Coloniality”, Transmodernity: Journal of Peripheral Cultural Production of the Luso-Hispanic World, vol. 1, núm. 1, 2011, pp. 1-38.

Frantz Fanon, Los Condenados de la Tierra, Fondo de Cultura Económica de España, 2010.

Véase G.G. Sánchez y S.D. Sánchez, “La producción discursiva en torno al matrimonio homosexual: una lucha de resistencia”, revista electrónica Discurso y Sociedad [http://www.diss{oc.org/ediciones/v10n02/DS10(2)Sanchez&Saldana.pdf].

Michel Guillen, Cinco ecuaciones que cambiaron el mundo. El poder y la oculta belleza de las matemáticas, México, Debolsillo, 2015, p. 61.

John Locke, Ensayo sobre el entendimiento humano, Mexico, Fondo de Cultura Económica, 1992, p. 210.

Joel Flores Rentería, “Justicia y derechos humanos”, Política y Cultura, primavera 2011, núm. 35, México, UAM-Xochimilco, p. 29.

Referencias

J. Galtung, Violencia cultural, Gernika-Gogoratuz, p. 13 [https://es.slideshare.net/villamarcos/violencia-cultural-johan-galtung], fecha de consulta: 16 de mayo de 2014.

Will Durant, The Life of Greece, The Story of Civilization II, Estados Unidos, 1966, p. 163.

Notas