Artículos de reflexión
Confluence
Confluência
Confluence
Revista Latinoamericana de Etnomatemática, vol. 10, no. 1, 2017
Universidad de Nariño

This work is licensed under Creative Commons Attribution 4.0 International.
Received: 25 June 2016
Accepted: 24 November 2016
Abstract: This position paper argues that ethnomathematics, while not a curriculum (nor a discipline, that is why D’Ambrosio call it a program), is a confluence of ideas and concepts that may lead to different mathematics engagement of our students. Just as water swirls together from multiple sources, so does our cognition when many ideas are brought together, leading to a cognitive confluence. The definition of ethnomathematics, as coined by D’Ambrosio in 1985 sets the foundation. Scholarship from other disciplines is included, as these areas motivate new thinking, new questions, and new perspectives.
Keywords: Ethnomathematics, Literature Review, Cognitive Confluence.
Resumo: Este documento argumentativo discute que a etnomatemática, embora não seja um currículo (nem uma disciplina, é por isso que D'Ambrosio a denomina comoum programa), é uma confluência de ideias e conceitos que podem direcionar ao envolvimento matemático diferenciado de nossos alunos. Assim, da mesma maneira que a água forma redemoinhos a partir de fontes múltiplas, a nossa cognição também se desenvolve quando muitas ideias são reunidas e conduzidasa uma confluência cognitiva. A definição de etnomatemática, tal como foicunhada por D'Ambrosio, em 1985, estabeleceu as sua bases. O saber de outras disciplinas também é incluída, pois essas áreas motivam novos pensamentos, novas questões e novas perspectivas.
Palavras-chave: Etnomatemática, Revisão de Literatura, Confluência Cognitiva.
1. Introduction
I recently heard the word confluence and considered this could serve as a metaphor for the state of ethnomathematics today. The flowing together of water and the flowing together of ideas, it seems the dynamic nature of the water as it comes together with its swirling action is a nice way to reflect on the history of the ethnomathematics program. I will even go so far as to argue that the cognitive confluence metaphor that is suggested has as one of its outcomes altruism. The confluence of these ideas is the foundation of this paper.
D’Ambrosio (1985) defines ethnomathematics in his seminal piece “Ethnomathematics and its Place in the History and Pedagogy of Mathematics.”
... We will call ethnomathematics the mathematics which is practiced among identifiable cultural groups, such as national-tribal societies, labor groups, children of a certain age bracket, professional classes, and so on. Its identity depends largely on focuses of interest, on motivation, and on certain codes and jargons which do not belong to the realm of academic mathematics. We go even further in this concept of ethnomathematics to include much of the mathematics, which is currently practiced by engineers, mainly calculus, which does not respond to the rigor and formalism developed in academic courses of calculus (p. 45).
Rosa & Orey (2016) identify six dimensions of ethnomathematics: cognitive; conceptual; educational; epistemological; historical; and political. Discussing the ethnomathematics program, they stated:
These dimensions show that the ethnomathematics program has an agenda that offers a broader view of mathematics that embraces ideas, processes, methods, and practices that are related to different cultural environments. This agenda leads to increased evidence of cognitive processes, learning capabilities, and attitudes that may direct the learning process occurring in our classrooms. In addition, reflecting on the dimensions of this program reveals that another important aspect of its agenda is to offer an important perspective for a dynamic and globalized modern society that recognizes that all cultures and all people develop unique methods and explanations that them to understand, act, and transform their own reality (p. 13).
Rosa & Orey (2016) do not suggest that the six dimensions are exhaustive. The “cognitive processes” lead to a cognitive confluence of ideas. As the ideas swirl it is revealed that these are not mutually exclusive events. Bishop’s (1991) six activities and borrowing etic and emic from the linguist Pike (1967), as well as the work of other scholars, begins to develop our perspective of how rich the confluence of ideas are and how this confluence may influence ethnomathematics as the scholarship matures.
2. Crafting the argument
Rosa & Shirley (2016) stated, “The main idea of an ethnomathematics program is an awareness of the many ways of knowing and doing mathematics to values, ideas, notions, procedures, and practices in a diversity of contextualized environments” (p. 1). Ethnomathematics scholarship has brought many “contextualized environments” to the forefront of awareness. While too numerous to list all of these a few might be worth being reminded of: Naresh’s (2012) work with Indian bus conductors; Massarwe, Verner, & Bshouty (2010) use of ornaments as an exploration of geometry through socio-cultural inquiry; and Staats (2006) engagement of anthropological examples as a motivator for studying mathematics.
Naresh’s (2012) research, while contributing to the mathematics education research in India, as importantly contributed to local mathematics “used in everyday situations” (p. 308). Naresh introduces the reader to “work-specific knowledge” (p. 329) that is focused upon bus conductors executing mental arithmetic based upon “fare stages, fare stage numbers and ticket prices” (p. 329). This spatial ability must be carried out quickly and correctly while considering the variables associated with this model of a passenger using this transportation service.
Massarwe, Verner, & Bshouty (2010) stated: “This experience inspired emotions, lively discourse, and learning motivation” (p. 1). The confluence of these elements is very desirable in the mathematics education of our learners. The ornaments and their respective construction are described using the codes and jargons of Western mathematics with an outcome that “students were emotionally affected by activities with ornaments connected with their own history and culture” (p. 9). Imagine outcomes in mathematics where students wanted the course extended and “inactive” (p. 17) students are enjoying themselves and actively engaging in their learning.
Staats (2006) challenges readers when she states: “If we are serious about understanding mathematics in local contexts of use, we must be willing to ask questions that do not seem mathematical in our own intellectual tradition” (p. 44). Staats described pedagogy is evidence of how mathematics education can “engage students who would otherwise drift through a class at minimum levels of achievement and interest” (p. 51). Through case study she was able to motivate students in mathematical explorations that did “not seem mathematical.” This dynamic process of ethnomathematics influencing pedagogy through a confluence of concepts that may not initially “fit” our notions of what is mathematics can lead to unexpected outcomes.
I doubt D’Ambrosio in 1977 (D’Ambrosio, 2016) could have seen the stage he was setting for an ethnomathematics program that nearly 40 years later has moved to an international level. D’Ambrosio (2016) discusses his response at ICME 3 to “Why teach mathematics?” to which he responded the “primary objective of mathematical education is to not perpetuate knowledge or to push existing knowledge further, which will go or fade away, but to foster the creation of new knowledge” (p. 5). I argue that the confluence of existing knowledge (this is the cultural dynamism or glocalization in a dialogical sense) lends itself to the creation of new knowledge.
Ethnomathematics is dynamic and changes very fast. Indeed, it is less conservative than academic mathematics. As long as new facts, phenomena, situations, and problems require ethnomathematics solutions, ethnomathematics will be alive. (D’Ambrosio, 2016, p. 7).
A dialogical, or glocal, approach to ethnomodelling research as put forth by Orey & Rosa (2015) “makes use of emic and etic knowledge traditions through processes of dialogue and interaction” (p. 364). The creation of new knowledge through dialogue and interaction might be best described by Orey & Rosa (2015) in their discussion of a glocal approach in ethnomodeling. In their view, outsiders build these models based on their reality while the insiders model is based on “their own reality” (p. 375). These two realities, emic and etic, potentially create knowledge for each, that is to say the emic reality is potentially new knowledge for the etic reality and vice versa.
When we stand on the shoulders of our predecessors we definitely see further and this improved view we have, if even for a fleeting moment, holds the potential for new knowledge. We are not restricted to the shoulders of our predecessors, we gain and share new knowledge from the contexts we study, with our searches of existing literature that suggests “new” confluences, and when we observe and listen to ‘knowledge, practices, language, and myths’ (D’Ambrosio, 2016) of groups of which we do not share membership. As D’Ambrosio (1985) shared, these can be professional classes (Hoyles, Noss, & Pozzi, 2001; Shockey, 1999, 2006), children (Nunes, Schliemann, & Carraher, 1993; Saxe, 1998), cultural groups (Shockey, 2006; Engblom-Bradley, 2006; Shockey & Mitchell, 2016), carpenters (Millroy, 1992) or carpet layers (Masingila, 1993). When new ideas and concepts come together, what emerges may be something of beauty, just as the Native people of the Maritimes have known for centuries, the confluence of fresh water and salt water is where the sweat grass grows (J. B. Mitchell, personal communication, November, 2016).
Bishop (1991) gave us six activities to consider: playing; designing and building; explaining; counting; measuring; and locating when looking at contexts. Shockey & Silverman (2016) extended this to seven by including calendar as one of the activities. Rosa & Orey (2016) have elaborated the “six dimensions of ethnomathematics” (p. 11) that support knowledge production (these six dimensions where elaborated on D’Ambrosio’s ideas of these dimensions). The ethnomathematics program produces knowledge that are “cognitive, conceptual, educational, epistemological, historical, and political” (p. 11-12). Bishop did not suggest that the activities were mutually exclusive and neither do Rosa and Orey. These scholars have put forth dynamic processes that serve as catalyst for new understandings. The benefit of these new ideas is discussions and changes to educational process and policy, all with the altruistic agenda of improving opportunities for children. Martin (2012) reminds us that our children are not commodities Citing the National Research Council (1989), the RAND Mathematics Study Panel (2003), and the U.S. Department of Education (2008), Martin states, “I also noted that the aims and goals of mathematics education for Black. children have often been conceptualized in overly simplistic ways that emphasize their commodification as future participants in higher-level mathematics courses or in the nation-preserving technological workforce” (p. 48). Ethnomathematics is not about the commodification of learners. As D’Ambrosio (2016) stated:
There is an increasing call for education in every small country, and ethnomathematics can contribute to addressing a number of the global challenges school systems face. Ethnomathematics is more acceptable to native populations and more accessible and affordable, mainly for those living rural and coastal areas. It appeals to traditional practices; hence, it is more attractive than the sometimes cold and austere formal mathematics in their existing programs (p. 6).
Bassanezi (1994) made a similar point when he stated:
To appreciate the human resources, explore and develop teachers’ and students’ skills, making them feel able to give the community their contribution and form socially active individuals. In other words try to follow Morley’s proposal: “Join your people and love them. Learn with them, plan with them and serve them. Start with what they already know. Build and teach them with what they have.” Teaching should deepen students’ knowledge, and for that they must be motivated to face mathematics not only as a science for its own sake but as an instrument for the understanding and possible modification of reality. (p. 31)
Zaslavsky (1994), talking about her correspondence with Raum (1938), who taught at Fort Hare University, in modern day Tanzania, “He stated that good teaching “lays down the importance of understanding the cultural background of the pupil and relating the teaching in school to it” (Raum, 1938, p. 5) (cited in Zaslavsky, 1994, p. 4).
2.1 Etic and Emic
“There are many groups of people who engage in mathematical thinking but who express it in their specific ways” (Ascher & D’Ambrosio, 1994, p. 42). If we recognize it as mathematical thinking, this the etic view that recognizes the emic view of their “specific ways.” The linguist Pike (1967) had motivations for his concepts of emic and etic that was not mathematically related. Discussing his 1947 research, Pike (1967) “…emic systems and emic units of these systems are in some sense to be discovered by the analyst, not created by him. Etic systems, on the other hand, are assumed to be classifications created by the analyst…”(p. 55-56). In 2002 Bassanezi stated:
The ethnomodelling process starts with the social context, reality, and interests of students and not by enforcing a set of external values and decontextualized activities without meaning for the students. This process is defined as the mathematics practiced and elaborated by different cultural groups, which involves the mathematical practices present in diverse situations in the daily lives of diverse group members. (2002, p. 208)
The “discovery” of the practices in the “daily lives” constitutes are the emic that Pike (1967) brought forward. The “enforcing of external values” is the etic and as each scholar suggests, order is important, emic than etic. Rosa & Orey (2013) modernization of Pike’s concepts states:
“The emic perspective provides internal conceptions and perceptions of mathematical ideas and concepts while the etic perspective provides the framework for determining the effects of those beliefs on the development of the mathematical knowledge…An emic-etic perspective includes a respect for alternative epistemologies, and of holistic and integrated natures of the mathematical knowledge of members of diverse cultural groups…”(p. 126).
Scholarship across decades provides another confluence with an outcome of respect.
As we consider the role of emic and etic, Whorf (1956b) told us that “We are all mistaken in our common belief that any word has “exact meaning”” (p. 258). Kluckhohn (1949), quoting Sapir:
But in any society as Edward Sapir said, Forms and significances which seem obvious to an outsider will be denied outright by those who carry out the patterns; outlines and implications that are perfectly clear to these may be absent to the eye of the onlooker. (p. 36)
Whorf (1956a) on talking:
…”the linguistic relativity principle,” which means in informal terms, that users of markedly different grammars are pointed by their grammars toward different types of observations and different evaluations of externally similar acts of observation, and hence are not equivalent as observers but must arrive at somewhat different view of the world. (p. 221)
Bishop (1994) stated:
I believe it is important to make a more radical assumption, namely that all formal mathematics education is a process of cultural interaction, and that every child experiences some degree of cultural conflict in that process. This I believe is a plausible assumption to make, on the basis that schools are different social institutions from others such as homes, that have been established to do what homes and other institutions cannot do… (p. 16).
As scholars in Ethnomathematics we share a responsibility that Kluckhohn (1949) acknowledged for anthropologists, “the first responsibility of the anthropologist is to set down events as seen by the people he is studying” (p. 299-300).
Writing about science education for First Nation students, Aikenhead (1997) stated:
“Learning science is viewed as culture acquisition that requires First Nations students to cross a cultural border from their everyday world into the subculture of science…. Cross-cultural instruction requires teachers to identify cultural border crossings for students and to facilitate those border crossings by playing the role of tour guide, travel agent, or culture broker, while sustaining the validity of students’ own culturally constructed ways of knowing” (p. 217).
The “everyday world”, emic, and the “subculture of science”, etic, must be considered when we discuss engagement of our learners in mathematics. Aikenhead (1997) sees the negotiation of these crossings as “essential,” and cites the work of Hennessy (1993) to acknowledge that the crossing of domains “ is exceedingly hard” (p. 225). Earlier work by Peat (1994, p. 42) (cited in Aikenhead, 1997, p. 225); “…the experience of border crossing by a Western physicist into a First Nations worldview was also described in terms of thinking differently: we should all learn to talk and listen together without prejudgment, learn to suspend our prejudices, and allow our consciousness to flow along new lines.” Our awareness of the inside (emic)/outside (etic) perspectives situates us to collaborate with students as they “navigate transitions” between their community and the academy.
Costa (1995), cited in Aikenhead (1997, p. 226), brings five categories for consideration as students move into the subculture of science.
These patterns in the ease with which students move into the subculture of science were de- scribed in terms of familiar student characteristics, and then clustered into five categories (summarized here in a context of cultural border crossing): (1) “Potential Scientists” cross borders into school science so smoothly and naturally that the borders appear invisible; (2) “Other Smart Kids” manage their border crossing so well that few express any sense of science being a foreign subculture; (3) “‘I Don’t Know’ Students” confront hazardous border crossings but learn to cope and survive; (4) “Outsiders” tend to be alienated from school itself and so border crossing into school science is virtually impossible; and (5) “Inside Outsiders” find border crossing into the subculture of school to be almost impossible because of overt discrimination at the school level, even though the students possessed an intense curiosity about the natural world” (p. 226).
These categories raise new questions for consideration in ethnomathematics through the interchange of the word “science” above with mathematics. As this perspective is considered, a potentially new confluence of ideas emerges.
In an academic environment, engaging the emic, etic perspectives, reveals what Lipka, Sharp, Adam, & Sharp (2007) has defined as the “third space.” Lipka’s third space is an outcome of Gee’s (1996) work where he discusses crossing “borderlands.” Likpa et al. (2007):
Gee’s (1996) concept of borderlands describes the space where two cultures or linguistic styles meet but co-evolve into a practice that is not strictly either and becomes a new creation. This is theoretically important. Classrooms have the potential for being these “third spaces:” not necessarily those of the dominant culture, nor in a one-to-one correspondence with the local Indigenous or ethnic minority culture. These third spaces have the potential to become productive uncharted zones between school and local cultural knowledge and norms. From a critical pedagogical perspective, this third space has the potential for changing historically situated authority structures. (p. 97)
“Co-evolving” is a unique confluence that presents opportunities in ethnomathematics.
When Leap (1981) was studying the Isletan Tiwa language for words that were fractions as recognized by Western academics:
I asked her if were possible to reduce the recipe and bake fewer loaves. “Certainly,” she replied (again in Tiwa), “start with half as much flour and you get half as many loaves.” “What adjustment would you have to make,” I asked, “if you wanted to bake only two or three loaves?” The question produced a thoughtful silence, and finally a comment: “why would you want to do that?” (p. 206)
“Why would you want to do that?” has become a mantra for looking in. What does it mean to “look in?” In an Ethnomathematics context, this is the outsider looking in on a phenomena occurring within a group for which the researcher is not a member. Many of us working in Ethnomathematics “look in” to begin to understand, possibly from the insiders’ view, but likely from the academic view. Reciprocity requires that we continue our dialogue with the group under study to make sure we are representing their way of knowing respectfully and correctly. In Aikenhead’s (2001, p. 338) discussion of students’ experiences of “enculturation into Western science is experienced as an attempt at assimilation into a foreign culture” he cautions us “students generally reject assimilation into the culture of Western science.” Ethnomathematics must understand this caution; the ethnomathematics program is not a program of assimilation.
3. Confluence with Learners
Ms. Kuohn (personal communication, April 2016) shared the following insights from her classroom. The episode was focused on students’ generalization of the sum of the interior angles in a polygon, 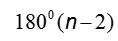 . A student in the class shared an “easier” way when he explained the following:
. A student in the class shared an “easier” way when he explained the following:
‘First, draw a shape, then place a point inside it’ (see Figure 1)
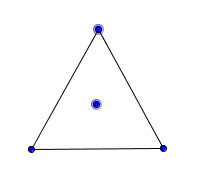
Figure 1
Triangle with interior point
Source: Own production
‘Now draw lines from each vertex to this inside point’ (see Figure 2)
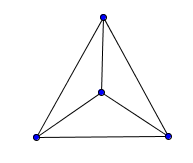
Figure 2
Connecting interior point to vertices
Source: Own production
‘Now you have three triangles, each has one hundred eighty degrees, so there are five hundred forty degrees. Look at the point inside, there are three hundred sixty degrees around that point, so subtract that and you get one hundred eighty.’ (see Figure 3)
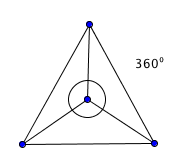
Figure 3
Sum of interior angles is 3600
Source: Own production
Ms. Kuohn drew more illustrations of the interaction where the child showed multiple examples of how his method “worked.” (see Figure 4)
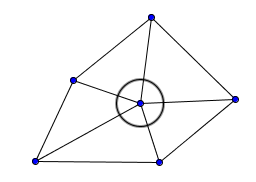
Figure 4
Beginning to generalize
Source: Own production
180°(5)-360°=540° Maybe “Two-Eyed Seeing” can be generalized to a child’s view? This strategy satisfies the generalization mentioned above. What occurred here was a learning moment for the teacher, she had not considered this problem with this pictorial representation as her student had. This was an important pedagogical moment. This is not the “banking model” described by Freire (1996), it may be: “The teacher is no longer merely the-one-who-teaches, but one who is himself is taught in dialogue with the students, who in turn while being taught also teach” (p. 61).
Shockey, Orey & Rosa (2015) described ethnomathematics in Ouro Preto, Brasil. During the ethnomathematics tour, students explored local artifacts “looking for” mathematics. One such occurrence was in an amphitheater where students walked to toe to heel to measure the circumference and diameter of the theater floor. Of course the ratio revealed nice approximations for pi. ‘Looking for mathematics,’ through a Western lens, was a new experience for this group of graduate students. Within the floor of this amphitheater was a square grid, comprised on smaller squares, see Figure 5. This was not “seen” as mathematical in particular when the students were asked about the generalization.

Figure 5
Sum of odd consecutive whole numbers
Source: Own production
Surprise emerged from the students when they realized the grid could serve as a model for the sum of consecutive odd numbers, 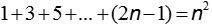 , (see Figure 5).
, (see Figure 5).
Shockey & Mitchell (2016) highlighted the importance of body dimensions as units of measure in the construction of a Penobscot lodge. While the base of the lodge was a product of two wingspans, two radii, an outcome was the height of the lodge being tall enough for people to stand. Understand the distance across a circle was also revealed in the discussion of creating roofing materials from tree bark. It was revealed that a log about a foot across would yield a piece of bark about three feet wide, 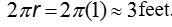 feet.
feet.
The dynamic nature of ethnomathematics (D’Ambrosio, 1985) serves as a lens to consider situations from the past as well as today. When Ascher (2002) brought “pullis kolam” to the attention of ethnomathematics, she brought forward the cultural significance.
The women and girls of a traditional Tamil Nadu household begin their day by sweeping the floor and the area in front of the house, sprinkling the threshold area with a solution made with cow dung, and then decorating the threshold area with kolam. The women are familiar with numerous designs – some for daily use, some for special occasions, and some for particular rituals and holidays. Girls are taught the designs and techniques by their mothers. It is an important part of a girl’s training, as kolam skills are considered a mark of grace and a demonstration of dexterity, mental discipline, inner harmony, and an ability to concentrate. The elaborate threshold decorations, which are built with basic designs and techniques, are aesthetic and creative expressions of the women who “place” them. (Ascher, 2002, p. 163)
In 2002 when Ascher revealed the confluence of culture and teaching between mother and daughter, as a trained mathematician, brought forward the discussion symmetries associated with kolam. Symmetries construct a pedagogical bridge between culture and Western mathematics. Ascher also shared the programming work of Gift Siromoney, who with his wife worked in “picture languages” (p. 168).
The languages are, essentially, concise statements of algorithms, or formulas for creating kolam. They make us more aware that the kolam are careful constructions with definable growth patterns. It is important to keep in mind, however, that the computer scientists are concerned with analyzing and generating the figures, and are not necessarily replicating the techniques or thought processes used by the Tamil Nadu women. (Ascher, 2002, p. 168)
Prior to Ascher’s work, Gerdes (1999) was investigating “sona” in Africa. Parallel to Ascher’s findings, Gerdes’ research revealed how these sand drawings “refer to proverbs, fables, games, riddles, animals, and so forth and play an important role in transmitting knowledge and wisdom from one generation to the next” (p. 158).
Boys would learn the sand drawing during their schooling in the “mukanda initiation rites” (p. 158). “To facilitate memorizing the standardized drawings the akwa kuta sona (those who know how to draw) invented the following mnemonic device: after cleaning and smoothing the ground, a drawing expert first sets out, with the tips of the index, or middle or ring fingers of his right-hand an orthogonal net…”(p. 158). As Gerdes discussed the cultural significance of the sona and the passing of knowledge, his descriptors included the procedures that upon completion he discusses using the language of Western mathematics. The symmetries as described in the language of mathematics, one or two axis of symmetry, or rotational symmetries, “The high frequency of sand drawings with one or more axes of symmetry constitutes an expression of the importance of (axial) symmetry within the culture of the Chokwe and related peoples” (p. 161).
Professor Sekhar Pindoprolu (personal communication, April 2016) shared that in his region of India the threshold designs are called “Muggulu.” In our discussion, he shared that these are “culturally different in areas of India.” He agreed that this is a way of “living harmoniously” as Ascher (2002) stated. The rice flour for making the design was a “gift to the ants and other insects, not killing nature, but to feed the ants and insects, and also keeps things from coming into the house.” He continued sharing that today much of the Muggulu are now designs that are part of contests during Sankaranthi festivals. Cow dung has been found to serve as antiseptic and is being studied by scientists to better understand its properties. An outcome of modernization in India is concrete. Dr. Pindoprolu recalls his mum sweeping the threshold and creating a Muggulu, but today thresholds are concrete and many times a Muggula design is painted on the concrete, defeating the purpose of the “gift.” He shared that this is a common practice today in rural areas. Below are five “Traditional Muggulu” shared by Mrs. Pindoprolu (personal communication April 2016). Not only do these serve as a mnemonic for the stories passed down from mother to daughter, but they could also serve as a pedagogical bridge between the academic classroom and community.

Figure 6
Traditional Mugullu (Pindoprolu)
Source: Own production
Figure 6 reveals rotational symmetry about the center point for multiple elements as well as a vertical symmetry in this muggulu. An etic view of Figure 6, decomposes the image into its mathematical components. Using the “pen” feature in GeoGebra, students can explore these motions. First, placing a vertical line in the image and then tracing elements with the “pen” feature that are going to be reflected about the vertical line has the potential to open student led discussions.
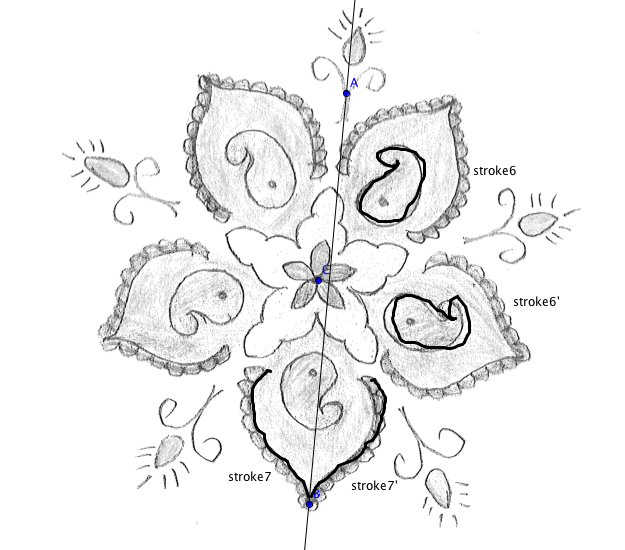
Figure 7
Traditional Mugullu (Pindoprolu)
Source: Own production
In Figure 7, stroke 7 (the GeoGebra naming
of pen strokes) is reflected about 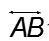 to reveal its image, stroke 7’. Stroke 6 has
image stroke 6’ after a rotation about center point C of 720.
to reveal its image, stroke 7’. Stroke 6 has
image stroke 6’ after a rotation about center point C of 720.
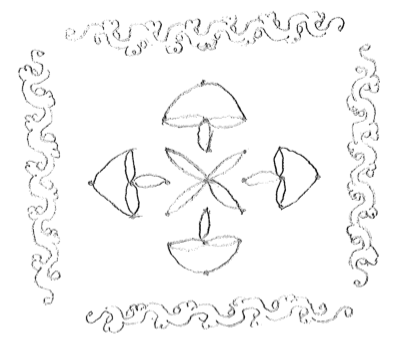
Figure 8
Traditional Mugullu (Pindoprolu)
Source: Own production
Observe the reflectional and rotational symmetries of Figure 8.
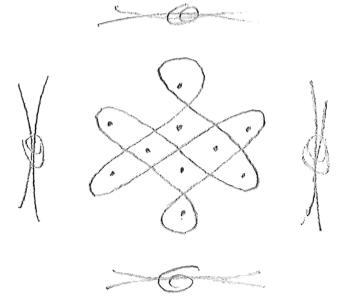
Figure 9
Traditional Mugullu (Pindoprolu)
Source: Own production
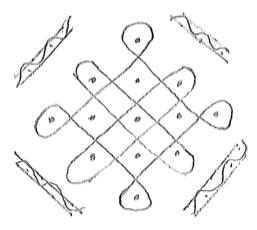
Figure 10
Traditional Mugullu (Pindoprolu)
Source: Own production
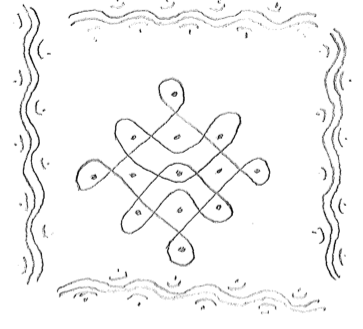
Figure 11
Traditional Mugullu (Pindoprolu)
Source: Own production
Figures 9, 10 and 11 all have explorable symmetries for students. Below, Figure 12 is decomposed into elements for consideration of the existing symmetries.
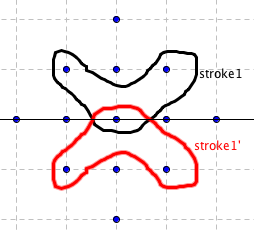
Figure 12
Decomposition of Figure 11
Source: Own production

Figure 13
Decomposition of Figure 11
Source: Own production
Figure 13 depicts two lines of symmetry for the outer portion of the mugullu. Figures 9, 10, 11 can be viewed as graphs, with even nodes. Each one of these figures is traceable without lifting your pencil or copying over a segment. These too can lead to discourse exchanges in the classroom that make connections.
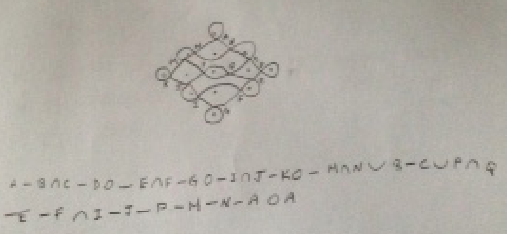
Figure 14
An algorithm for tracing
Source: Own production
Labeling the nodes as shown in Figure 14, could lead to students creating a coded algorithm for their respective path. For the path shown in Figure 14, a U denotes the path went under a point, an inverted U denotes the path went over a point, and a – denotes a straight segment from one node to another. These Muggulu align with the findings and suggestions of the work of Ascher (2002) and Gerdes (1999). Engaging this local knowledge in the creation of a pedagogical bridge, it is important to avoid divorcing this from it original intention. Local, traditional practices are important for making connections.
A confluence of the emerging concepts that Gerdes (1999) brought forward may have important educational implications. Gerdes suggests sona as a framework for educational investigations of symmetry, arithmetic progressions, greatest common divisors and elementary graph theory explorations. At the 2012 Canadian Mathematics Education Study Group’s Annual Meeting, the author and others were told a beautiful story by Paulus as he drew the representative lusona on a chalkboard, it was mesmerizing.
4. Concluding remarks
The confluence of ideas and concepts generated in Ethnomathematics emerge from many dynamic sources. This confluence is evident when Orey & Rosa’s (2015) stated: “Ethnomathematics is a program of study that allows for understanding, comprehension, articulation, processing, and ultimately the use of mathematical ideas, procedures and practices that allow us to solve problems related to our daily lives” (p. 367). The swirling effect of the sources, once an element of calmness begins, is altruism, altruism that has respect at its core value. “The important point that ethnomathematics adds, however, is that, nonetheless, expressions of mathematical ideas do have content and cultural context” (Ascher & D’Ambrosio, 1994, p. 39).
Taking liberty with Bing’s (1957) remark on teachers’ content knowledge, I would like to suggest that a teachers’ content is contextually inclusive as well. “A teacher’s knowledge of the subject should extend well beyond the material in the course. He does not want to be like the boy who fell out of bed – he went to sleep to near where he got in” (p. 307). Being contextually inclusive is not an original suggestion as Jaworski (2008) stated that mathematics teacher educators “need to know mathematics, pedagogy related to mathematics, mathematical didactics in transforming mathematics into activity for learners in classrooms, elements of educational systems in which teachers work including curriculum and assessment, and social systems and cultural settings with respect to which education is located” (p. 1).
Removing physical boundaries allows students to experience mathematics as they find it. This could occur at the Indain threshold where a Muggula was created, in Africa on smoothed dirt to study a lusona, or walking about in Brasil and looking for pi. Allowing students to lower and/or remove mental barriers permits them to realize that mathematics is not just what happens in their textbook, they can ask questions that maybe do not fit their reality of what is mathematics, questions that open up new avenues of mathematical explorations
References
Aikenhead, G. (1997). Toward a First Nations cross-cultural science and technology curriculum. Science Education , 81, 217-238.
Aikenhead, G. (2001). Integrating western and Aborignal sciences: Cross-cultural science teaching. Research in Science Education , 31, 337-355.
Ascher, M. (2002). Mathematics elsewhere: An exploration of ideas across cultures. New Jersey: Princeton University Press.
Ascher, M., & D’Ambrosio, U. (1994). Ethnomathematics: A dialogue. For the Learning of Mathematics , 14(2), 36-43.
Bassanezi, R. (1994). Modelling as a teaching-learning strategy. For the Learning of Mathematics , 14(2), 31-35.
Bassanezi, R. C. (2002). Ensino-aprendizagem com modelagem matemática [Teaching and learning wit mathematical modelling] . São Paulo: Editoria Contexto.
Bing, R. H. (1957). Point set topology. In F. Staf (Ed.), Insights into Modern Mathematics , vol. 23 (pp. 306-335). Washington, D.C.: NCTM.
Bishop, A. J. (1991). Mathematical enculturation. Dordrecht, The Netherlands: Kluwer Academic Publishers.
Bishop, A. J. (1994). Cultural conflicts in mathematics education: Developing a research agenda. For the Learning of Mathematics , 14(2), 15-18.
Costa, V. B. (1995). When science is "another world": Relationships between worlds of family, friends, school, and science. Science Education , 79, 313-333.
D'Ambrosio, U. (1985). Ethnomathematics and its place in the history and pedagogy of mathematics. For the Learning of Mathematics--An International Journal of Mathematics Education , 5(1), 44-48.
D'Ambrosio, U. (2016). An overview of the history of Ethnomathematics. In M. Rosa, U. D’Ambrosio, D. C. Orey, L. Shirley, W. V. Alangui, P. Palhares, & M. E. Gavarrete (Autores), Current and future perspectives of Ethnomathematics as a program (pp. 5-10), New York: Springer
Engblom-Bradley, C. (2006). Learning the Yup'ik way of navigation: Studying time, position, and direction. Journal of Mathematics and Culture , 1(1), 90-126.
Freire, P. (1996). Pedagogy of the oppressed. London: Penguin.
Gee, J. P. (1996). Social linguistics and literacies: Ideology in discourses (2nd ed.). London; Bristol, PA: Taylor & Francis.
Gerdes, P. (1999). Geometry from Africa: Mathematical and educational explorations. USA: Mathematical Association of America.
Hoyles, C., Noss, R., & Pozzi, S. (2001). Proportional reasoning in nursing practice. Journal for Research in Mathematics Education , 32(1), 4-27.
Jaworski, B. (2008). Mathematics teacher educator learning and development. In B. Jaworski & T. Wood (Eds.), The International Handbook of Mathematics Teacher Education Volume 4: The Mathematics Teacher Educator as a Developing Professional (pp. 1-13). Vol. 4, Rotterdam: Sense Publishers.
Kluckhohn, C. (1949). Mirror of man . New York: McGraw Hill Book Company Inc.
Leap, W. L. (1981). Does Indian math (still) exist? The Journal of the Linguistic Association of the Southwest , 4(2), 196-213.
Lipka, J., Sharp, N., Adams, B., & Sharp, F. (2007). Creating a third space for authentic biculturalism: Examples from math in a cultural context. J ournal of American Indian Education , 46(3), 94-115.
Martin, D. B. (2012). Learning mathematics while Black. The Journal of Educational Foundations , 26(1-2), 47-66.
Massarwe, K., Verner, I., & Bshouty, D. (2010). An ethnomathematics exercise in analyzing and constructing ornaments in geometry class. Journal of Mathematics and Culture , 5(1), 1-20.
Masingila, J. O. (1993). Learning from mathematics practice in out-of-school situations. For the Learning of Mathematics , 13(2), 18-22.
Millroy, W. L. (1992). An ethnographic study of the mathematical ideas of a group of carpenters . Reston: National Council of Teachers of Mathematics.
Naresh, N. (2012). Bus conductors' use of mental computation in everyday settings - is it their ethnomathematics?. Journal of Mathematics and Culture, 6(1), 308-332.
National Research Council. (1989). Everybody counts: A report to the nation on the future of mathematics education. Washington, DC: National Academy Press.
Nunes, T., Schliemann, A., & Carraher, D. (1993). Street mathematics and school mathematics. New York: Cambridge University Press.
Orey, D. C., & Rosa, M. (2015). Three approaches in the research field of ethnomathematics: Emic (local), etic (global, and dialogical (glocal). Revista Latinoamericana de Etnomatemática , 8(2), 364-380.
Peat, D. (1994). Lighting the seventh fire . New York: Carol Publishing Group.
Pike, K. L. (1967). Language in Relation to a Unified Theory of the Structure of Human Behavior. The Hague, Paris: Mouton.
RAND Mathematics Study Panel. (2003). Mathematics proficiency for all students: Toward a strategic research and development program in mathematics education. Santa Monica, CA: RAND.
Raum, O. F. (1938). Arithmetic in Africa . London: Evans Bros.
Rosa, M., & Orey, D. C. (2013). Ethnomodelling as a research lens on ethnomathematics and modelling. In G. Stillman, G. Kaiser, W. Blum & J. Brown (Eds.), Teaching mathematical modelling: Connecting to research and practice (pp. 117-130). New York: Springer.
Rosa, M., & Orey, D. C. (2016). State of the art in Ethnomathematics. In M. Rosa, U. D’Ambrosio, D. C. Orey, L. Shirley, W. V. Alangui, P. Palhares, & M. E. Gavarrete (Autores), Current and future perspectives of Ethnomathematics as a program (pp. 11 - 38), New York: Springer.
Rosa, M., & Shirley, L. (2016). Introduction. In M. Rosa, U. D’Ambrosio, D. C. Orey, L. Shirley, W. V. Alangui, P. Palhares, & M. E. Gavarrete (Autores), Current and future perspectives of Ethnomathematics as a program (pp. 1 - 4), New York: Springer
Saxe, G. B. (1988). Candy selling and math learning. Educational Researcher , 17(6), 14-21
Shockey, T. L, (1999). The mathematical practices of a group of thoracic cardiovascular surgeons. Unpublished Dissertation. University of Virginia, Charlottesville, VA.
Shockey, T. L. (2006). Left Ventricle Reduction through an Ethnomathematics Lens. For the Learning of Mathematics: An International Journal of Mathematics Education , 26(1), 2-6.
Shockey, T.L, Orey, D., & Rosa, M. (2015) A Spring Ethnomathematics Tour in Brasil. Notices of the North American Study Group on Ethnomathematics , 8 (1), 8 – 11.
Shockey, T. L., & Mitchell, J. B. (2016). An ethnomodel of a traditional penobscot summer dwelling. International Journal for Research in Mathematics Education , 6(1), 178-195.
Shockey, T. L, & Silverman, F. L. (2016). Ten Years Later: A Look Back on the History of the Journal of Mathematics and Culture. Journal of Mathematics and Culture, 10(2), 12-36.
Staats, S. (2006). The Case for Rich Contexts in Ethnomathematics Lessons. Journal of Mathematics and Culture , 1(1), 39-56
U.S. Department of Education. (2008). Foundations of success: Final report of the national mathematics advisory panel. Washington, D.C.: U.S. Government Printing Office.
Whorf, B. L. (1956a). Linguistics as an exact science. In J. B. Carroll (Ed.), Language, thought and reality: Selected writings of Benjamin Lee Whorf (pp. 220-232). Cambridge, MA: The M.I.T. Press.
Whorf, B. L. (1956b). Language, mind, and reality. In J. B. Carroll (Ed.), Language, thought and reality: Selected writings of Benjamin Lee Whorf (pp. 246-270). Cambridge, MA: The M.I.T. Press.
Zaslavsky, C. (1994). Africa Counts and ethnomathematics. For the Learning of Mathematics , 14(2), 3-8.
Author notes