Introducción

La creación del concepto de criptomonedas ha causado un gran impacto tanto desde el punto de vista comunicacional como comercial, debido a varias razones: Se presenta como un medio de pago más económico, incluso por debajo del SWIFT⁽¹⁾, la tarjeta de crédito; es una muestra más del carácter fungible del dinero en general; es discreto, asertivo, e instantáneo; es impersonal e individual; tiene un gran potencial de desarrollo; es cuantificable y puede ser convertible; y preserva lo que todo tipo de dinero tiene y es el de ser un símbolo (Navalpotro, et al., 2003;Simmel, 2004; Olivo 2011).

No obstante, este medio de pago tiene algunas desventajas: Cierto grado de desconfianza por su novedad, errores del software, virus informáticos, el papel de los keyloggers y la posibilidad de capturar contraseñas, menoscabo en la confianza del protocolo P2P (Peer to Peer), ser un medio de actividades financieras ilícitas, entre otras (European Central Bank [ECB], 2015).

Desde un punto de vista más cercano a la economía política, es un espacio de confrontación de agentes con competencia para lograr el dominio del mundo de las finanzas en particular y la economía en general. Esto queda demostrado con el surgimiento de movimientos que respaldan a las criptomonedas y quienes lo adversan. En el primer grupo se encuentra, entre otros: El anarcocapitalismo⁽²⁾y el Agorismo⁽³⁾.

No obstante, en este artículo, se pretende dar cuenta del mercado de criptomonedas desde la perspectiva de la teoría monetaria. Mediante el empleo de datos mensuales de los últimos 67 meses, desde enero de 2014 hasta julio de 2019 del Bitcoin; se procederá a realizar una investigación de carácter descriptivo del tipo ex post facto(Kothari, 2004), con la finalidad de describir el funcionamiento del mercado de criptomonedas y mostrar la relación entre el desempeño del Bitcoin en términos del teorema de la regresión de Mises (1982) y de la teoría de la demanda de dinero de Friedman (1956).

1. Revisión de la literatura

Al conceptualizar el mercado de las criptomonedas, es ineludible comenzar con una definición al menos de carácter etimológico. Así, criptomoneda es una palabra compuesta por Κρύφιος que significa oculto, escondido (Pabón y Echauri, 1967a) y moneda proviene del latin Moneta (medio para facilitar los intercambios. Ahora bien, el adjetivo virtual proviene del latin virtῡs(Pabón y Echauri, 1967b) o aquello que tiene la virtud de realizar algún efecto de manera implícita o tácita. Es decir, la criptomoneda es un medio de intercambio/inversión que se hace efectivo mediante un cifrado y un descifrado por medio de claves (del latin clavis) (Pabón y Echauri, 1967b) y sin la presencia cara a cara, física, de dos agentes económicos. Por su parte el Banco Central Europeo BCE (European Central Bank, ECB) hace la siguiente definición de criptomonedas:

A los efectos de este informe, se define como una representación digital de valor, no emitida por un banco central, entidad de crédito o entidad de dinero electrónico, que en algunas circunstancias puede utilizarse como alternativa al dinero. El término "esquema (s) de moneda virtual" se utiliza a lo largo de este informe para describir tanto el aspecto del valor como el de los mecanismos inherentes o incorporados que garantizan que el valor se pueda transferir. (ECB, 2015, p.4).

Al respecto, Huang, Huang y Ni (2019) sostienen que la primera criptomoneda descentralizada del mundo es el Bitcoin, que ha llegado a ser la más conocida, utilizada mundialmente, y en consecuencia cuya cotización sirve de referencia a las demás criptomonedas.

Silva, et al. (2019), comentan que Bitcoin comenzó en enero de 2009 y constituye una moneda digital que elimina la necesidad de un tercero para validar la ejecución de pagos. De acuerdo a Urdaneta, et al. (2019a), la criptomoneda minada la producen programadores que cuentan con equipos como los ASIC (Circuito Integrado para Aplicaciones Específicas), con el propósito de resolver las estructuras cada vez más complejas de bloques blockchain. Esa resolución permite concluir la transacción de manera segura. Por eso Wang, et al. (2019), consideran al blockchain como uno de los inventos más emocionantes en la comunidad de la información y la tecnología de comunicación durante la última década.

Ahora bien, mucho ha sido el cuestionamiento acerca de la carencia de un marco regulatorio para el mercado de la criptomoneda. Sin embargo, de acuerdo a Shanaev, et al. (2019), se ha evidenciado reacciones positivas sobre la propuesta de un marco regulatorio y el reconocimiento legal, aunque la existencia de regulaciones promueve movimientos de precios negativos.

Además, entre los atributos más notables que ofrecen las criptomonedas resumidos por Sobhanifard y Sadatfarizani (2019) se encuentran: 1) Las transacciones internacionales a muy bajo costo; 2) alta velocidad de transacción, descentralización de la moneda garantiza su seguridad (Silva, et al., 2019); 3) servicio las veinticuatro horas del día; 4) fuera del control de un gobierno o banco central; 5) el anonimato de los usuarios; 6) lo difícil de su rastreo confiable (Dibrova, 2016); y, 7) para Caporale, Gil-Alana y Plastund (2018), el mercado de Bitcoin es sensible, puesto que reacciona inmediatamente a la llegada de nueva información.

Aunque el mercado de criptomonedas es muy joven, tiene suficientes datos disponibles, que hacen atractivo su estudio para determinar sus propiedades y comportamiento (Caporale, et al., 2018). Por ello, Huang, et al. (2019), señalan que el mercado Bitcoin, está compuesto por diferentes factores que influyen en el nivel de precios de la criptomonedas como el volumen de transacciones y el monto de las criptomonedas emitidas por el sistema.

Ahora bien, este trabajo busca dar cuenta del mercado de las criptomonedas desde la perspectiva de la teoría cuantitativa del dinero y el denominado “teorema de la regresión” (Mises, 1982). En el caso de la teoría cuantitativa del dinero, Fisher y Brown (2007) definieron dinero: “como aquello que es generalmente aceptado en el intercambio de bienes” (p.8). Estos autores clasificaron el medio circulante en dos categorías: Efectivo, constituido por monedas (coins), billetes de bancos (bank notes), transferencias (transferts) y cuentas postales (post-office); y depósitos bancarios (bank deposits).

Así, Fisher y Brown (2007) relacionaron: 1) El nivel agregado de precios P; 2) la cantidad de dinero en circulación M; 3) la velocidad de circulación del dinero V⁽⁴⁾; y 4) el volumen de comercio o el monto de bienes adquiridos con dinero T. Es decir, la teoría cuantitativa del dinero podía ser mejor explicada por medio de la ecuación de cambio⁽⁵⁾. En consecuencia, el total de adquisiciones realizadas por la economía en un año sería M.V + M´.V´. En consecuencia, la nueva ecuación de cambio sería: M.V + M´.V´ = Σp.Q = P.T. Al incluir M´.V´ con relación a P.T, el equilibrio en la ecuación de cambio hará que se incremente P. En consecuencia, Fisher y Brown (2007) introducen E´= M´.V´⁽⁶⁾.

En la Universidad de Chicago, el economista Milton Friedman desarrolló un trabajo sobre la teoría monetaria, del cual se origina su obra Studies in the Quantity Theory of Money (Friedman, 1956). El autor toma del desarrollo previo de la ecuación de cambio y hace su propuesta referida a la demanda de dinero por parte de las empresas que se condensa en la siguiente expresión:

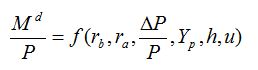(1)

Así, según Salerno (2010), la demanda de dinero quedaría determinada: 1) Por los costos de los servicios productivos del dinero; 2) la tasa de rendimiento del dinero y otros activos; 3) por el tamaño del volumen de ventas, producción total de las empresas; y 4) por factores tales como las expectativas. De esta manera, de acuerdo con Friedman (1956), la demanda de los saldos monetarios en término reales es una función que depende de forma inversa del rendimiento (r_a y r_b) de otros activos financieros alternativos (bonos y acciones) y de la tasa esperada de cambio de precios 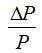, y de forma directa la renta permanente Y_p, tomada como índice de la riqueza total y de la proporción de riqueza humana respecto a la no humana, h. La variable u representa todo el conjunto de factores no especificados, que hacen referencia a las preferencias, expectativas, entre otros, y cuya incidencia directa o inversa no es posible predecir a nivel agregado.

No obstante, para los efectos del presente estudio, es necesario resaltar algunos aspectos de la teoría cuantitativa del dinero que se pueden relacionar con el mercado de las criptomonedas, entre los que se encuentran: 1) La relación directa entre la cantidad de dinero existente y el comportamiento de los precios; 2) el cambio en los agregados monetarios utilizados por los agentes económicos se hace notar fundamentalmente en los precios; 3) los determinantes en el nivel general de precios son la oferta monetaria, la velocidad de circulación del dinero; 4) el volumen de transacciones; y 5) el valor de las criptomonedas está sujeto a las leyes de oferta y demanda del mercado⁽⁷⁾.

Otro elemento a considerar en el mercado de las criptomonedas y su comportamiento es el teorema de regresión de Mises (1982) va más allá de Menger (2007) al demostrar que, lógicamente, el dinero sólo puede hacerse como producto de procesos catalácticos voluntarios (Salerno, 2010). Para Mises (1982), en el intercambio indirecto la función primaria del dinero es el de ser medio de intercambio y al estudiar el valor de los bienes es falso que el dinero mida sus valores y precios. Por su parte, Urdaneta, et al. (2019b) sostienen que “el dinero para mantenerlo debe ser medio de cambio y depósito de valor” (p.118). El poder adquisitivo del dinero tiene dos fuentes: “El valor de uso subjetivo” y el “valor de cambio objetivo” (Mises, 1982). Aquí el asunto es como determinar el valor de cambio objetivo, puesto que cuando coincide con el valor de uso subjetivo se tiene el valor de cambio objetivo.

Empleando el concepto de utilidad marginal de manera intertemporal, para evitar lo que se conoce como “circular argument” (Mises, 1982, p.113) o círculo austríaco (Rothbard, 1990);Mises (1982) consideró que en la alineación de las preferencias de bienes y servicios se consideran a los bienes de primer grado. Las valoraciones son independientes de la fijación de los precios de mercado, puesto que el dinero no se demanda para su uso directo, sino para adquirir bienes. Ahora bien, la confluencia colectiva de utilidades marginales ante la disponibilidad de bienes, determina que para un primer periodo el valor de uso subjetivo se iguale al valor de cambio objetivo. Para un segundo periodo.

Lo anterior es lo que se conoce como el “teorema de la regresión” (Mises 1982). La demanda de dinero hoy estará en función del poder adquisitivo del dinero en el periodo anterior (transacción anterior incluso), que implica un equilibrio entre oferta y demanda de dinero en el periodo anterior. La demanda de dinero dependerá del poder adquisitivo del dinero en el periodo anterior y la utilidad marginal del dinero ahora.

El logro de Mises (1982) fue demostrar, sin caer en la falacia del argumento circular, que la planificación de la demanda del dinero puede explicarse usando la teoría de la utilidad marginal y que esta tiene una curva descendente, como cualquier otro bien⁽⁸⁾. Además, demostraba que los agentes económicos demandan dinero para intercambios futuros. Está comprendida por una demanda de intercambio por aquellos que desean obtener dinero y una demanda de reserva por aquellos que lo poseen, tal como lo manifiestan Davidson y Block (2015).

Puede verse que el teorema incluye dos elementos distintos. La primera parte, es una explicación causal-realista de la utilidad marginal del dinero, mientras que la segunda, es una explicación causal-genética que trata el origen del dinero. El segundo elemento explica por qué no hay una regresión infinita y cómo la economía pasa de un estado en el que solo hay intercambio directo (un estado de trueque) a uno en el que está presente el intercambio indirecto (Davidson y Block, 2015).

En el caso del Bitcoin, según Davidson y Block (2015), está planteado un debate, respecto a si el mismo representa un medio de intercambio y se ajusta a lo planteado en el teorema de la regresión de Mises (1982); esto puede producirse de dos maneras: Bien porque Bitcoin tiene realmente un valor anterior a convertirse en medio de intercambio, o porque la teoría permite que este valor abarque un bien intangible.

2. Resultados y discusión

El presente estudio busca construir un conocimiento explícito sobre el mercado de las criptomonedas como activo financiero para las mipymes, con el fin de mejorar sus niveles de competitividad, utilizando datos mensuales de los últimos 67 meses desde enero de 2014 hasta julio de 2019. Las variables de entrada utilizada en la fase de insumos según la metodología, son el precio del cierre del Bitcoin, la capitalización del mercado, el volumen de las transacciones y la cantidad de criptomonedas emitidas. La modelización se realizó mediante la aplicación de regresiones polinomiales de segundo grado, donde las variables fueron convertidas a logaritmos de Briggs. La variable independiente, en el eje de las abscisas, es la cantidad de criptomonedas emitidas; mientras que en el eje de las ordenadas se ubican: La capitalización del mercado, el volumen de las transacciones y el precio de cierre (ver Gráfico I).

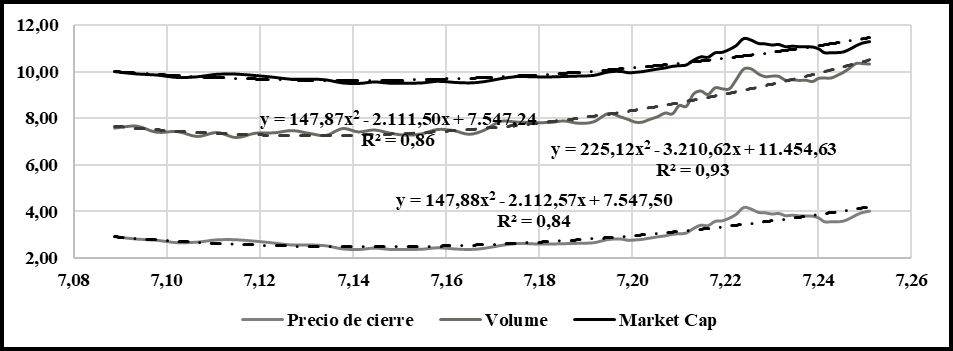
Gráfico I:
Variables del mercado
Elaboración propia, 2020

En el Gráfico I, se puede destacar la evolución ascendente de cada una de las variables, teniendo como hecho relevante que los coeficientes de las ecuaciones de regresión tanto en el precio de cierre, como capitalización del mercado, son similares; lo cual evidencia un alto grado de asociación como se muestra en la Tabla 1. Asimismo, se puede notar que en la medida que aumenta la cantidad de criptomonedas emitidas, se incrementa el valor de cada una de las variables dependientes en mayor cuantía, cuyos coeficientes de elasticidad son 16,45 respecto al precio de cierre, 15,98 en el volumen de las transacciones y 5,51 con la capitalización del mercado; evidenciándose un componente de elasticidad total, donde una variación del 1% en las criptomonedas emitidas, se traduce en una variación del 16,45% del precio de cierre; 15,98% del volumen de las transacciones y 5,51% en la capitalización del mercado.

Tabla 1
Correlación de variables de mercado

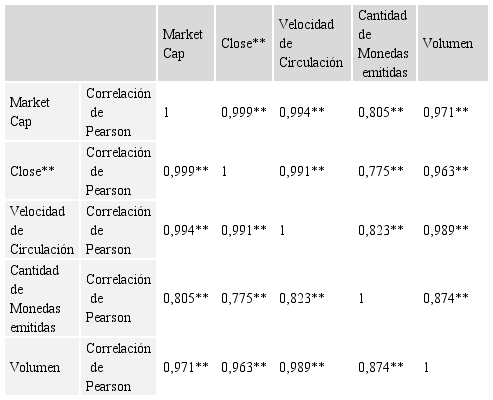
Elaboración propia, 2020. ** La correlación es significativa en el nivel 0,01 (bilateral).

		Market Cap	Close**	Velocidad de Circulación	Cantidad de Monedas emitidas	Volumen
Market Cap	Correlación de Pearson	1	0,999**	0,994**	0,805**	0,971**
Close**	Correlación de Pearson	0,999**	1	0,991**	0,775**	0,963**
Velocidad de Circulación	Correlación de Pearson	0,994**	0,991**	1	0,823**	0,989**
Cantidad de Monedas emitidas	Correlación de Pearson	0,805**	0,775**	0,823**	1	0,874**
Volumen	Correlación de Pearson	0,971**	0,963**	0,989**	0,874**	1

En la Tabla 1, se observa un alto grado de asociación lineal entre las variables del mercado, pero los resultados más relevantes para los efectos del presente estudio se encuentran el de la cantidad de criptomonedas emitidas y el precio de cierre del 77,5%, explicando el 84% de su varianza de acuerdo al Gráfico I. En el mismo orden, se encuentra la capitalización del mercado cuyo grado de asociación lineal es del 80,5% pero al mismo tiempo explica el 86% de su variación, ver Gráfico I; en lo que respecta al volumen de transacciones, existe un 87,4% de asociación lineal, mientras que explica el 93% de su varianza.

Ahora bien, en la Tabla 1 está la variable velocidad de circulación del dinero V en logaritmo base 10. Para los efectos de la presente investigación P (Precio del cierre del bitcoin), T (Volumen de transacciones) y M (Capitalización del mercado), se evidencia que existe un alto grado se asociación del 82,3% respecto a la cantidad de criptomonedas emitidas (Bitcoin); sumado a ello de acuerdo al Gráfico II, esta última explica el 89,31% de la varianza.

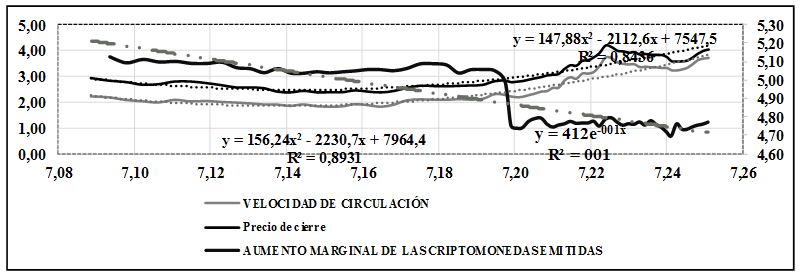
Gráfico II:
Aumento marginal de criptomonedas, velocidad de circulación y precio de cierre
Elaboración propia, 2020.

En lo que respecta al Gráfico II, este explica cómo ha funcionado el mercado de las criptomonedas, el cual consiste en un aumento de las criptomonedas emitidas, como consecuencia del incremento del volumen de transacciones, esto a su vez provoca un acrecentamiento de los precios y la velocidad de circulación; pero de forma contraria, se produce una disminución marginal exponencial del -62% respecto a las criptomonedas emitidas el mes anterior, razón por la cual se eleva cada vez más su precio en forma tendencial.

De igual manera, en el Gráfico III se muestra la función que describe la evolución de los Bitcoin emitidos durante 67 meses sujetos a estudio en logaritmo base 10. Ahora bien, existe un tope en el que no puede haber más 21.000.000 de Bitcoin emitidos en log10 (21x106) = 7,32; bajo estas condiciones, el tiempo que tardaría en alcanzar la meta . Entonces, el polinomio quedaría 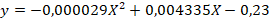que bajo el criterio de la primera derivada queda 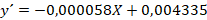maximizando la función, se iguala a cero 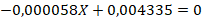se despeja .

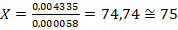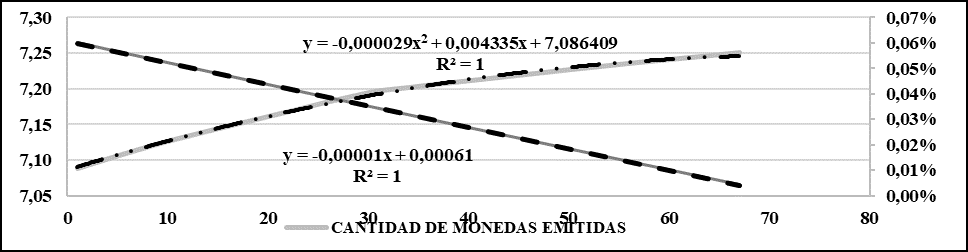
Gráfico III:
Aumento marginal de criptomonedas y las criptomonedas emitidas
Elaboración propia, 2020.

Asimismo, se plantea la función que denota la tasa de crecimiento de dicha función 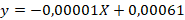, mostrando una pendiente decreciente, es decir, a medida que aumenta el número total de criptomonedas emitidas, disminuye su tasa de crecimiento. Razón por la cual surge una interrogante dada la función de la cantidad de monedas emitidas, ¿Cuándo esta alcanzará su tope y en qué tiempo bajo estas condiciones? Para responder a la misma se calculó el vértice de la curva que describe dicha función: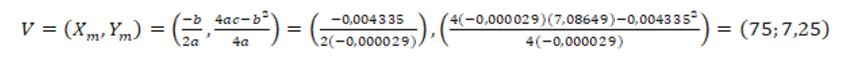

Otra forma de estimar este punto es maximizando la función de la tasa de crecimiento, igualándola a cero y sustituyendo Xm, en la ecuación de la tasa de crecimiento 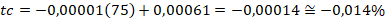la tasa de crecimiento sería cero. Con lo cual en el mes 75 alcanzaría bajo estas condiciones el tope máximo de emisión de criptomonedas.

Lo que pudiera ocurrir en estos casos para que el sistema pueda alargar un poco más la emisión, es que disminuya la tasa de crecimiento, con lo cual si aumentan el volumen de las transacciones suba el precio, o se produzca una bifurcación de Bitcoin (Fork) de la red blockchain creando nuevos proyectos partiendo de uno anterior, como para actualizar un proyecto en cuestión, antes de llegar a dicho tope antes señalado.

Es decir la tasa de crecimiento del precio respecto al volumen de transacciones es 16% según lo mostrado en el Gráfico IV, pero presentando un componente de inelasticidad, es decir, una variación de 1% del volumen de las transacciones se traduce en una variación del 0,86% de los precios. Asimismo, la tasa de crecimiento del volumen respecto al tiempo es para el periodo analizado 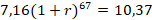; ; 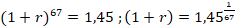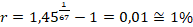esto quiere decir que en los próximos 8 meses el volumen de las operaciones podría crecer 100%(1+0,01)8-100% = 8,29% y el precio de las criptomonedas, 100%(1+0,0086)8-100% = 7,09% bajo las condiciones actuales, con tasas de crecimiento mensual del 1% para el volumen de transacciones y 0,86% para los precios.

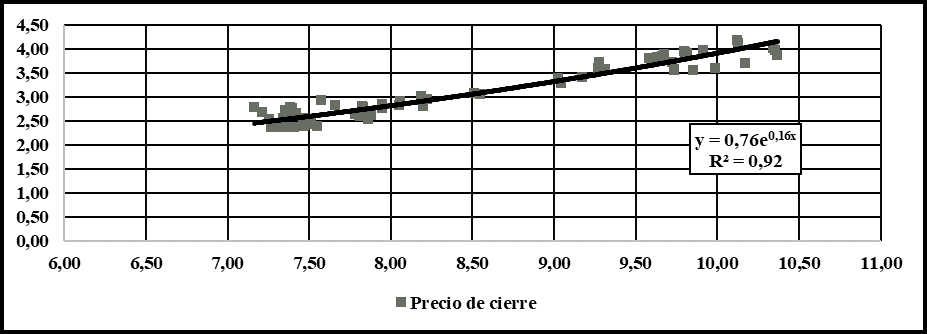
Gráfico IV:
Crecimiento del precio de las criptomonedas respecto a volumen de transacciones
Elaboración Propia, 2019.

Lo anteriormente expuesto coincide con lo planteado por Mises (1982) en relación a su “teorema de la regresión”. Así, el valor del Bitcoin (precio cierre promedio) en el mes M, es igual al poder adquisitivo del mes anterior M-1, tal como se muestra en la Tabla 2, donde el valor de la media es positivo y se encuentra dentro de los intervalos de confianza de la diferencia al 95%, es decir el precio de cierre presente es mayor al precio de cierre del mes anterior en términos promedios, aunque dicha diferencia no sea significativa debido a que el Sig. (Bilateral)>0,05; ello pudiera explicarse a la buena coordinación del mercado en sus variables.

Tabla 2
Prueba de muestras emparejadas entre el precio de cierre presente y anterior

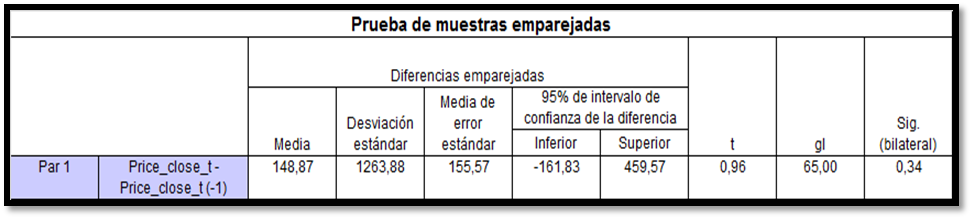
Elaboración propia, 2020.

En la Tabla 3, se observa que existe un alto grado de asociación lineal de 0,94 es decir 94% mientras que el mismo explica el 88% de la variable dependiente precio de cierre en el mes actual PCt; la misma presenta un incremento constante mensual de 233,99 dólares, más el 97% del valor del precio de cierre mensual anterior, los residuos del modelo son completamente independientes puesto que el estadístico Durbin-Watson está ubicado en los límites dL=1,43 y dU=1,49 con un nivel de significancia del 1% con un intervalo de confianza del 99%. El modelo es significativo para la predicción, debido a que el valor de Fcalculado= 472,83, como el de Tcalculado= 21,74 son significativos por ser mayores a sus valores teóricos Fteórico= 7,077 Tteórico= 7,05.

Tabla 3
Indicadores de significancia del modelo

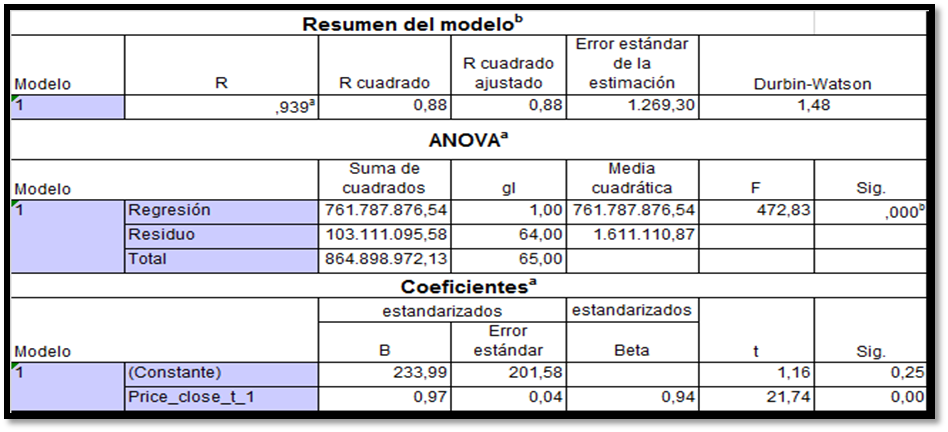
Elaboración propia, 2020.

El Gráfico V con variables a nivel, muestra que la prospección del precio promedio de cierre del mes anterior respecto al precio de cierre del mes presente, se comporta con una tendencia creciente (ver pendiente de la recta de regresión), en que el 88% de la variación del precio promedio de cierre del mes actual es explicado por el precio promedio de cierre del mes anterior.

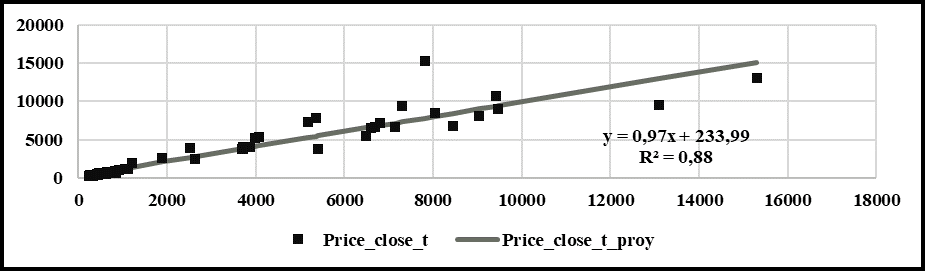
Gráfico V:
Prospección del precio de cierre del mes Pt y Pt (proyectado) en función del precio de cierre del mes Pt-1
Elaboración Propia, 2020.

De igual manera, en el Gráfico VI se evidencia con la estimación de las variaciones promedios, como en el primer cuatrimestre del año el mercado de Bitcoin se contrae en sus variaciones de precio, capitalización de mercado y volumen de transacciones en febrero y abril. Por otra parte, la cantidad de criptomonedas se expande y el volumen de transacciones también, aunque solo en enero y marzo. Mientras en el segundo cuatrimestre del año, hay una recuperación de las variaciones de precio, capitalización de mercado y volumen de transacciones, sobre todo en mayo y junio. Pero en julio y agosto se contrae nuevamente. En dicho lapso la emisión de Bitcoin se desacelera en su crecimiento entre marzo y diciembre.

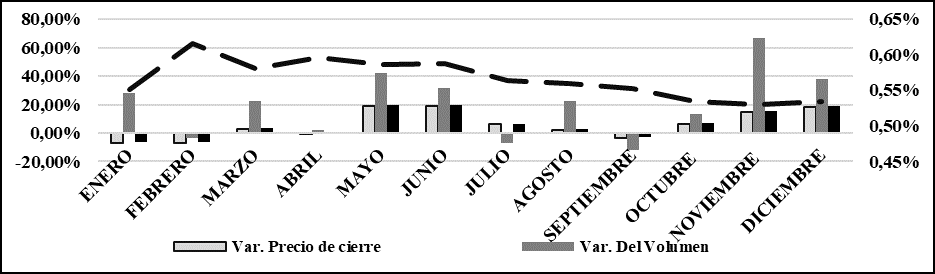
Gráfico VI:
Evolución de las variaciones de precios de cierre, capitalización del mercado, volumen de transacciones y criptomonedas emitidas mensualmente en el periodo 2014-1 al 2019-7
Elaboración Propia, 2020.

Finalmente, en el último cuatrimestre del año, con la excepción del mes de septiembre, donde culmina la contracción del mercado que inicia julio, a partir del mes de octubre el mercado comienza a expandirse, en cuando a incremento de precios, volumen de transacciones y capitalización del mercado; no así la emisión de criptomonedas, la cual evoluciona en forma contraria al resto de las variables del mercado, todo en aras de revalorizar el precio de los Bitcoins por las razones de la oferta y la demanda, debido a que crece el volumen de transacciones (demanda) y disminuye progresivamente la tasa de crecimiento del aumento marginal de Bitcoin.

Conclusiones

En el trabajo se demostró que existe, al menos desde el punto de vista estadístico, una relación plausible entre el comportamiento del mercado de las criptomonedas y supuestos que sostienen la teoría monetaria de Friedman (1982) y especialmente en relación al denominado teorema de la regresión (Mises, 1982).

Lo anterior permite aseverar de que es posible: 1) Hacer teoría monetaria con las criptomonedas; 2) uno de los resultados será que la definición operativa de dinero, el cual es ya problemática (Mishkin, 2008) deberá sufrir una seria transformación; y 3) desarrollar política monetaria con ellas. Esa posibilidad estaría abierta en la medida en que los Estados nacionales, que ejercen señoreaje con sus monedas, decidan intervenir este mercado en la medida en que se puedan, entre otras cosas: 1) Realizar un uso cada vez más extendido de las criptomonedas; 2) que surjan problemas que afecten la seguridad y calidad de las operaciones; 3) como producto de lo anterior, se produzca un incremento preocupante en delitos relacionados con el uso de este sistema de medio de pago y de inversión.

Finalmente, el trabajo de investigación se ajustó a la metodología del enfoque sistémico planteado al inicio. En la fase de insumos, se establecieron las variables del mercado de la criptodivisa para ser analizada, posteriormente en la fase de procesamiento, se estimó la variable velocidad de circulación del dinero con base a los postulados de la teoría cuantitativa del dinero, se modeló el aumento marginal de criptomonedas, velocidad de circulación del dinero y su precio de cierre; con la finalidad de explicar el funcionamiento del mercado, mediante funciones de regresión polinómica y exponencial.

Se estimó y modelo mediante el empleo de funciones de regresión polinomial y lineal del aumento marginal de las criptomonedas emitidas y las criptomonedas emitidas calculadas como el cociente entre la capitalización del mercado y el precio de cierre. Seguidamente, se valuó y simuló el crecimiento del precio de las criptomonedas respecto a volumen de transacciones, demostrando cómo la emisión de criptomonedas evoluciona en forma contraria al resto de las variables del mercado, todo en aras de revalorizar el precio de los Bitcoins por las razones de la oferta y la demanda, debido a que crece el volumen de transacciones (demanda) y disminuye progresivamente la tasa de crecimiento del aumento marginal de Bitcoin.

Referencias bibliográficas

Cantillon, R. (2002). Essai sur la nature du commerce in Général. Essay on the Nature of Trade in General. Liberty Fund, Inc.

Caporale, G. M., Gil-Alana, L., y Plastun, A. (2018). Persistence in the cryptocurrency market. Research in International Business and Finance, (46) 141-148. https://doi.org/10.1016/j.ribaf.2018.01.002

Davidson, L., y Block, W. (2015). Bitcoin, the regression theorem, and the emergence of a new medium of exchange. Quarterly Journal of Austrian Economics, 18(3), 311-338.

Dibrova, A. (2016). Virtual currency: New step in monetary development. Procedia-Social and Behavioral Sciences, 229, 42-49. https://doi.org/10.1016/j.sbspro.2016.07.112

Dupuit, J. (1952). On the measurement of the utility of public works. International Economic Papers, (2), 83-110. Recuperado de

European Central Bank - ECB (2015). Virtual currencies schemes: A further analysis. ECB. https://op.europa.eu/en/publication-detail/-/publication/96fe84e9-3d29-4790-a1a4-d89218c244ac/language-en

Fisher, I., y Brown, H. G. (2007). The purchasing power of money: Its determination and relation to credit interest and crises. Cosimo Classics.

Friedman, M. (1956). The quantity theory of money: A restatement. In M. Friedman (Ed.), Studies in the quantity theory of money (pp. 3-21). University of Chicago Press.

Huang, J-Z., Huang, W., y Ni, J. (2019). Predicting bitcoin returns using high-dimensional technical indicators. The Journal of Finance and Data Science, 5(3), 140-155.

Konkin, E. S. (2006). New libertarian manifesto. KoPubCo.

Kothari, C. R. (2004). Research methodology: Methods and technics. New Age International Publishers.

Menger, C. (2007). Principles of economics. CreateSpace Independent Publishing Platform.

Mises, L. V. (1982). The theory of money and credit. Liberty Fund, Inc.

Mishkin, F. S. (2008). Moneda, banca y mercados financieros. Octava edición. Pearson Educación.

Navalpotro, J. S., Hierro, J. D. U., Cáceres, J. I., y Freire, M. T. (2003). Teorías y modelos macroeconómicos. Esic Editorial.

Olivo, V. T. (2011). Tópicos avanzados de teoría y política monetaria. Editorial Arte Profesional.

Pabón, J. M., y Echauri, E. (1967a). Diccionario manual griego. Griego clásico-español. Primera edición. Vox.

Pabón, J. M., y Echauri, E. (1967b). Diccionario Manual de Latin. Primera edición. Vox.

Rothbard, M. N. (1990). La teoría austriaca del dinero. Revista Libertas, (13), 1-19.

Salerno, J. T. (2010). Money, sound & unsound. Ludwig von Mises Institute.

Shanaev, S., Sharma, S., Ghimire, B., y Shuraeva, A. (2020). Taming the blockchain beast? Regulatory implications for the cryptocurrency market. Research in International Business and Finance, 51, 101080. https://doi.org/10.1016/j.ribaf.2019.101080

Silva, M. J., Almudhaf, F. W., Miranda, B., Silveira, A. B., Franco, D. G., Sobreiro, V. A., y Kimura, H. (2019). Can artificial intelligence enhance the Bitcoin bonanza? The Journal of Finance and Data Science, 5(2), 83-98. https://doi.org/10.1016/j.jfds.2019.01.002

Simmel, G. (2004). Philosophy of money. Psychology Press.

Sobhanifard, Y., y Sadatfarizani, S. (2019). Consumer-based modeling and ranking of the consumption factors of cryptocurrencies. Physica A: Statistical Mechanics and its Applications, 528, 121263. https://doi.org/10.1016/j.physa.2019.121263

Urdaneta, A. J., Borgucci, E. V., Campuzano, J. A., y Avilés, P. A. (2019a). Hechos estilizados del mercado de criptomonedas desde el enfoque de la eficiencia marginal del capital. Visionario Digital, 3(2), 228-244. https://doi.org/10.33262/visionariodigital.v3i2.421

Urdaneta, A., Borgucci, E., Morán, G., y Farinango, R. (2019b). Dolarización de la economía venezolana desde el enfoque de la demanda de dinero. Revista de Ciencias Sociales (Ve), XXV(E-1), 114-129. https://dx.doi.org/10.31876/rcs.v25i1.29602

Wang, L., Shen, X., Li, J., Shao, J., y Yang, Y. (2019). Cryptographic primitives in blockchains. Journal of Network and Computer Applications, 127, 43-58. https://doi.org/10.1016/j.jnca.2018.11.003

Notas