Espacios de trabajo matemático. Puntos de vista y perspectivas
Spaces for Mathematical Work: Viewpoints and perspectives
Espaces de travail mathématique. Points de vue et perspectives
Espacios de trabajo matemático. Puntos de vista y perspectivas
Revista Latinoamericana de Investigación en Matemática Educativa, vol. 17, 4-1, pp. 5-39, 2014
Comité Latinoamericano de Matemática Educativa

Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.
Resumen: Este número especial de la Revista Latinoamericana de Investigación en Matemática Educativa (RELIME) es el resultado de distintos artículos elaborados para el tercer simposio Espacio de Trabajo Matemático (ETM), cuyo objeto de estudio es el desarrollo y los usos posibles de la noción de ETM en la didáctica de las matemáticas. El trabajo matemático y su funcionamiento en el marco escolar están a la base del enfoque de los ETM. En esta introducción se sintetiza el enfoque teórico, no como algo prescriptivo sino como una propuesta sugerente para enriquecer el estudio didáctico del trabajo matemático del alumnado y profesorado. Seguidamente, se describe la organización temática de las contribuciones.
Abstract: This special issue of Revista Latinoamericana de Investigación en Matemática Educativa (RELIME) is dedicated entirely to the articles proposed within the framework of the third Symposium Mathematical Work Space (ETM, in French) which is devoted to the study, development and possible applications of the ETM concept in the didactics of mathematics. The mathematical work and its functioning within the school setting are the foundation of the ETM approach, and in this introduction, before presenting the thematic organization of the contributions; we will summarize this theoretical approach. Its goal is to enrich, in a non-normative manner, the didactic study of the mathematical work of the students and teachers
Résumé: Ce numéro spécial de la Revista Latinoamericana de Investigación en Matemática Educativa (RELIME) est entièrement issu des propositions d’articles élaborées dans la foulée du troisième symposium Espace de Travail Mathématique (ETM) consacré à l’étude, au développement et aux usages possibles de la notion d’ETM en didactique des mathématiques. Le travail mathématique et son fonctionnement dans le cadre scolaire sont à la base de l’approche par les ETM et, dans cette introduction, avant de présenter l’organisation thématique des contributions, nous résumons cette approche théorique. Celle-ci se propose, de manière non normative, d’enrichir l’étude didactique du travail mathématique des élèves et des professeurs
Espacios de trabajo matemático. Puntos de vista y perspectivas
1. Una perspectiva didáctica sobre el trabajo matemático
A partir de la década de los sesenta se produjo un cuestionamiento fuerte de la enseñanza de las matemáticas a nivel mundial. Antes de este periodo, los sistemas escolares ofrecían dos tipos de enseñanza a los ciudadanos de los países desarrollados. Por una parte, una enseñanza corta y esencialmente utilitarista de las matemáticas elementales, propuesta a los niños de los contextos populares. Y por otra parte, a los niños de la burguesía, destinados a tomar las riendas de la economía y la gestión de los países, se les daba acceso a una enseñanza de las matemáticas vista como una escuela del razonamiento lógico. En ambos casos, al alumno se le hacía desempeñar el rol de receptor del saber de los maestros. A partir de los años sesenta, diversos fenómenos contribuyeron a cambiar los puntos de vista sobre el rol de las matemáticas y sobre la manera de enseñarlas. Sin querer ser exhaustivos, podemos señalar la reforma de las matemáticas modernas, el desarrollo de las investigaciones sobre los aprendizajes, o incluso, la masificación de la enseñanza, en un contexto de mayor competencia económica e ideológica.
Para nuestros fines, subrayaremos dos profundas características de los cambios que se acentuaron desde entonces: por una parte, hacer evidente la diversidad del trabajo del matemático visto como el motor principal de la evolución matemática y, por otra parte, la idea pedagógica de promover la actividad del alumno con miras a hacerlo más apto para desarrollar sus conocimientos en un contexto de resolución de problemas. En este caso, el trabajo matemático está en el corazón de la evolución, lo que lleva lógicamente a proporcionar a esta noción un lugar central en la didáctica de las matemáticas.
El trabajo al que nos referimos está basado en una actividad racional orientada hacia un objetivo particular que puede apoyarse o no en el uso de un cierto número de instrumentos y artefactos específicos. En matemáticas, el objetivo de esta actividad estará centrado en los objetos estudiados por los matemáticos, «estos seres humanos que hacen que avance la comprensión humana de las matemáticas» (Thurston, 1994, p. 162). Por lo tanto, consideramos que la investigación didáctica, en el marco de una enseñanza que favorezca el desarrollo del trabajo matemático del alumno, debe interrogarse sobre este trabajo desde el doble punto de vista del aprendizaje de los alumnos y de la organización de la enseñanza por el profesor.
2. La noción del Espacio de Trabajo Matemático
La noción general de Espacio de Trabajo Matemático (ETM) amplía la noción de espacio de trabajo para la geometría, introducida por Kuzniak y Houdement (Kuzniak, 2006) en el estudio de la didáctica de este ámbito. Esta noción se precisa con el objetivo de comprender mejor lo que, desde el punto de vista didáctico, se pone en juego alrededor del trabajo matemático en un marco escolar. El espacio concebido de esta manera designa un ambiente pensado y organizado que facilita el trabajo de los individuos al resolver problemas matemáticos. En el caso de las matemáticas escolares, estos individuos generalmente no serán expertos sino alumnos o estudiantes, bien a nivel de principiantes o avanzados. Del estudio inicial de este concepto en Geometría, conservamos el principio que articular el ETM en dos niveles (Kuzniak, 2011): uno de naturaleza epistemológica, en relación estrecha con los contenidos matemáticos del ámbito estudiado y, el otro, de naturaleza cognitiva, que concierne al pensamiento del sujeto que resuelve tareas matemáticas.
El trabajo matemático deriva, entonces, de un proceso que por una parte da sentido de manera progresiva, a cada uno de los niveles epistemológico y cognitivo y, por otra parte, permite la articulación de estos dos niveles gracias a diferentes génesis. En el caso de la Geometría, el conjunto del proceso se describió a partir de elementos del diagrama precisado en la Fig. 1. Éste necesitará ciertas modificaciones para adaptarlo al marco general de los ETM:
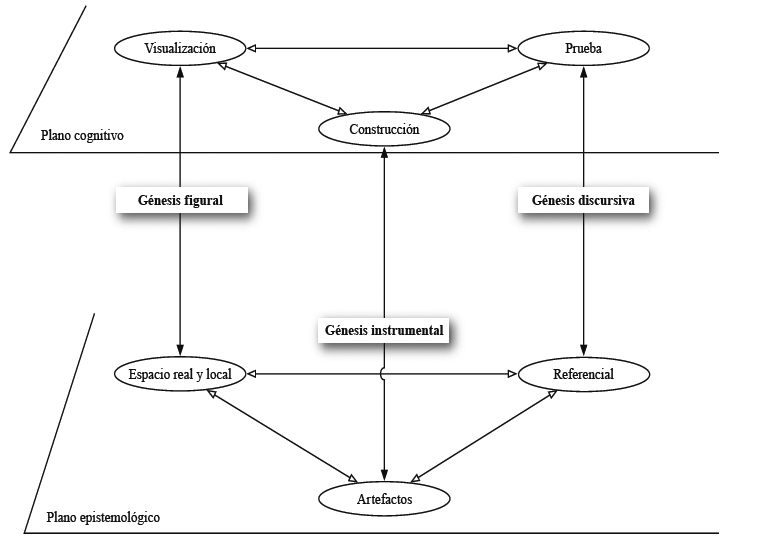
Figura 1
El espacio de trabajo geométrico y sus génesis
2.1. El nivel epistemológico y sus componentes
En lo que concierne a la Geometría, tres componentes en interacción son características de la actividad geométrica en su dimensión puramente matemática:
-
un espacio real y local como soporte material, con un conjunto de objetos concretos y tangibles;
-
un conjunto de artefactos como herramientas de dibujo o software;
-
un sistema teórico de referencia basado en definiciones y propiedades.
Estos componentes no están yuxtapuestos, deben ser organizados según un objetivo que depende del ámbito matemático en su dimensión epistemológica. Cuando el acento se pone en el proceso de aprendizaje del alumno, en una situación didáctica, este nivel epistemológico se puede considerar también como un medio epistemológico (Coutat & Richard, 2011).
Si los artefactos y el referencial teórico son dos componentes base del nivel epistemológico, asociado a un ámbito matemático particular, el componente ligado al espacio y a las configuraciones geométricas debería ser modificada si se quiere extender a otros ámbitos matemáticos. De acuerdo con una concepción de las matemáticas fundamentada en representaciones semióticas, que va más allá de la pura consideración de sistemas de representación, parece pertinente utilizar la noción de signo o representamen, en el sentido de Peirce. Así, el signo o representamen es “algo” que representa otra cosa, que sea su objeto o quizá él mismo. En función del ámbito matemático en cuestión, los signos podrán ser dibujos geométricos, símbolos algebraicos o gráficas, incluso fichas, maquetas o fotos, en el caso de problemas que ponen en juego la modelización. A diferencia de los signos de estructura diádica, tan habituales en matemáticas, la idea de un signo que también es su propia representación invita a considerar de otra manera el proceso semiótico cuando el trabajo matemático está en juego. Esto es especialmente visible cuando un dibujo geométrico, que es en sí mismo una forma, es a la vez representamen y modelo de representación (Coutat, Laborde & Richard, 2016).
2.2. El nivel de los procesos cognitivos
Las matemáticas que se enseñan no son un corpus desprovisto de propiedades y objetos reducidos a significantes manipulables mediante sistemas formales. De entrada, las matemáticas son principalmente una actividad humana. De esta manera, es esencial comprender cómo comunidades de individuos, pero también individuos particulares, utilizan y se apropian de los conocimientos matemáticos en sus prácticas de la disciplina. Asimismo, es esencial comprender cómo se va a dar sentido a estos signos y objetos tangibles, lo que implica un segundo nivel del ETM centrado en el sujeto, que a su vez, se contempla como sujeto cognitivo. Esta apertura hacia el campo cognitivo se debe realizar en estrecha relación con los componentes del nivel epistemológico y, para continuar en un marco didáctico, se efectúa una adaptación del enfoque semiótico propuesto por Duval (1995, 2005). Para la actividad geométrica, estos procesos son:
-
un proceso de visualización relativo a la representación del espacio y al soporte material;
-
un proceso de construcción que depende de los instrumentos utilizados (regla, compás, entre otros) y configuraciones geométricas en juego;
-
un proceso discursivo que produce argumentaciones y pruebas.
El proceso de visualización necesita ser precisado para encontrar su lugar en una extensión a los ETM. También se debe asociar a esquemas y operaciones de uso de los signos, de los que nada nos prueba que dependan, a priori, de la visualización en sí, incluso en una concepción extensa de ésta (Fig. 2).
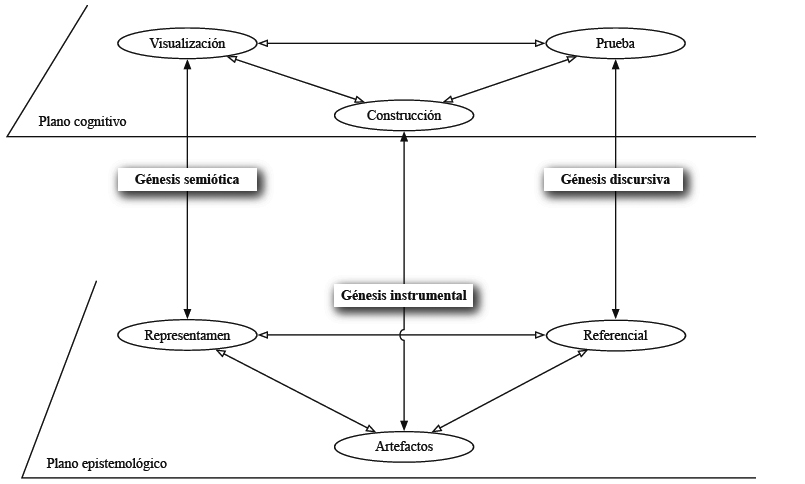
Figura 2
El espacio de trabajo geométrico y sus génesis
Este proceso de visualización «extensa» se debe distinguir de la simple visión o percepción de los objetos y se puede considerar como el proceso de estructuración de las informaciones aportadas por los diagramas y los signos. Además, este proceso alimenta la intuición de las propiedades y, a veces, fundamenta cognitivamente la validez de estas propiedades. Bajo ciertas condiciones, puede emparentarse con un razonamiento de tipo discursivo - gráfico (Richard, 2004) y podrá expresarse al interior de registros de representación semiótica determinados.
3. Los ETM de referencia, idóneos y personales
En el marco teórico de los ETM, así como en el de los Espacios de Trabajo Geométrico (ETG), la noción de paradigma orienta y estructura la organización de los componentes que, debido a sus diferentes funciones, participan en la especificidad de los diversos paradigmas en juego. Un paradigma se instituye cuando una comunidad de individuos acuerda formular problemas, así como organizar sus soluciones, privilegiando ciertas herramientas o ciertas formas de pensamiento. Al espacio de trabajo «paradigmático», tal como es definido por esta comunidad, se le llamará ETM de referencia. En una institución escolar dada, la resolución de un problema supone que un ETM idóneo se puede organizar para permitir a un alumno comprometerse en la resolución del problema. Este ETM idóneo debe necesariamente cumplir dos condiciones: por una parte, posibilitar el trabajo en el paradigma correspondiente a la problemática considerada; por otra parte, estar «bien construido», en el sentido en que sus diferentes componentes están organizados con criterios de validez. El diseñador desempeña un rol parecido al del arquitecto que diseña un espacio de trabajo para usuarios potenciales. En clase, el diseño de este espacio va a depender del ETM personal del profesor. Cuando el problema se propone a un alumno, el tratamiento matemático que éste le da lo conduce al ETM personal de este alumno. Debido a esto, el ETM idóneo no es fijo y se debe modificar continuamente para ajustarse a las restricciones locales.
De esta manera, el trabajo matemático en un marco escolar se puede describir gracias a tres niveles de ETM: la matemática considerada por la institución que se describe en el ETM de referencia, desarrollado por el profesor hasta alcanzar un ETM idóneo que permita un establecimiento efectivo en clase, donde cada alumno trabaja en su ETM personal.
La elección y la organización de las tareas propuestas a los alumnos por los profesores son esenciales en la constitución del ETM idóneo. Ofrece la posibilidad de resolver, de manera adecuada, lo que se les propone, es decir, conforme a las expectativas institucionales descritas de manera más o menos explícita en el ETM de referencia. Estas elecciones y la gestión de las actividades van a depender, en gran parte, del ETM personal del profesor. La observación de la actividad de los alumnos permitirá identificar sus ETM personales identificando posibles subconjuntos de prácticas estables.
4. Las génesis de los ETM
El desarrollo de un individuo de su trabajo matemático se lleva a cabo gradualmente y pasa por el establecimiento progresivo de su ETM personal. Esta génesis global del ETM supone un conjunto de génesis que son interdependientes y que involucran a todos los componentes epistemológicos y a los procesos cognitivos. La activación y el control de estas génesis se pueden iniciar por los profesores (en el nivel del ETM idóneo). Es importante saber en qué medida éstas se adecuan en su origen, a las expectativas definidas en el ETM de referencia (Kuzniak & Rauscher, 2011; Kuzniak, 2013).
Como lo vimos, los niveles epistemológico y cognitivo estructuran los ETM y ayudan a comprender la circulación de los conocimientos en el seno del trabajo matemático. ¿Cómo articular de manera operatoria los niveles epistemológicos y cognitivos con el fin de hacer posible el trabajo matemático esperado? Nos parece adecuado apoyarse en tres génesis fundamentales que derivan del marco teórico desarrollado previamente:
-
una génesis instrumental que hace funcional los artefactos en el proceso constructivo que contribuye al trabajo matemático;
-
una génesis semiótica basada particularmente en los registros de representación semiótica, que proporciona un sentido a los objetos del ETM y les confiere su estatus de objetos matemáticos operatorios; esta génesis semiótica asegura el establecimiento de la relación entre sintaxis, semántica, función y estructura de los signos vehiculados;
-
una génesis discursiva de la prueba que utiliza las propiedades en el referencial teórico para ponerlas al servicio del razonamiento matemático y de una validación no exclusivamente icónica, gráfica o instrumentada.
A fin de definir el trabajo geométrico en el marco de los ETG, Coutat y Richard (2011) describen las interacciones específicas del enfoque geométrico (ver Fig. 4) caracterizando los tres planos verticales que aparecen en el diagrama de los ETG. En nuestro afán por construir una teoría de los ETM que generalicen los saberes adquiridos en la investigación sobre los ETG, los planos verticales introducidos podrán conectarse con las diferentes fases del trabajo matemático implementado en la ejecución de una tarea: descubrimiento y exploración, justificación y razonamiento, presentación y comunicación. De hecho, la ejecución efectiva de estas fases definirá un cierto número de competencias matemáticas cognitivas fundamentadas sobre la base de la coordinación de las génesis y sus relaciones con el plano epistemológico (Fig. 3).
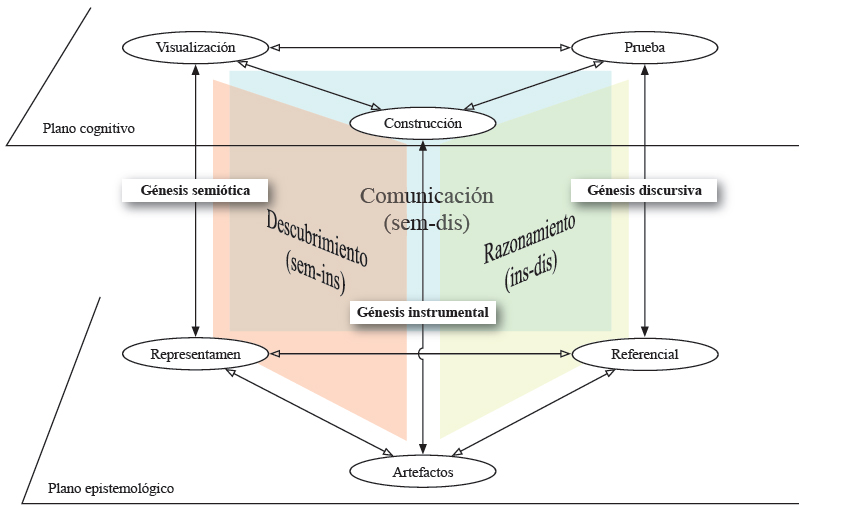
Figura 3
Los planos verticales en el ETM
Un primer tipo de interacciones privilegia la identificación y la exploración de los objetos apoyándose en las génesis semiótica e instrumental para desarrollar una competencia ligada al descubrimiento de la solución de problemas matemáticos. Un segundo tipo de interacciones desarrolla el razonamiento matemático fundado en la justificación de descubrimientos, que articula las génesis instrumental y discursiva. Finalmente, un último tipo está orientado hacia la comunicación matemática de los resultados y se apoya esencialmente en las génesis semiótica y discursiva. La definición exacta de estos planos de interacciones y la descripción de sus interrelaciones depende del ámbito matemático específico que se haya estudiado.
5. Temáticas de este número especial
El trabajo matemático confedera en este número el conjunto de contribuciones y constituye el centro científico alrededor del cual se ha cohesionado la comunidad científica que ha participado en los diferentes simposios. Sin restringirse a la elaboración de un Espacio de Trabajo Matemático en su sentido técnico, el objetivo de las conferencias elegidas en esta monografía se interrogan ampliamente acerca de las dimensiones semióticas, cognitivas e instrumentales del trabajo matemático, no excluyendo a priori ningún enfoque epistemológico o didáctico. Esta extensión de la problemática al trabajo matemático en un sentido amplio se propuso a los participantes desde los cuatro temas de reflexión especificados en este número.
Tema 1 - El trabajo matemático y los ETM
El objetivo de este tema es, por una parte, profundizar en el modelo teórico definido por los Espacios de Trabajo Matemático y, por otra parte, explorar las utilizaciones que como herramienta de análisis tiene en estudios específicos. Utilizar este modelo en otros ámbitos distintos al de la geometría conlleva un estudio particular y específico de los ámbitos en cuestión para ser aplicados en álgebra, análisis, aritmética, entre otros. Para armonizar las notaciones, estos espacios de trabajo específicos, asociados a dominios específicos D, se denotaran ETMD, es decir, ETMàlgebra, ETManàlisis, ETMaritmética, etcétera. El Espacio de Trabajo Matemático se puede entender como una red que ponga en relación las diversas fibras que constituyen los ETMà. La cuestión es saber, entonces, cómo se organizan la red de fibras entre espacios o la superposición de los planos. Estas interacciones entre los dominios específicos son esenciales para comprender el funcionamiento global del trabajo matemático y éstas obligarán, además, a considerar los procesos de modelización en el marco de los ETM, más allá de las puras cuestiones semióticas.
Tema 2 - Ambientes tecnológicos y trabajo matemático
Este tema se centra específicamente en la utilización de ambientes tecnológicos y en qué medida afectan el trabajo matemático. De hecho, la aparición reciente de numerosos instrumentos ha contribuido a dar un nuevo relieve a los aspectos constructivos y a los artefactos que sostienen la ejecución del trabajo matemático, tanto en el nivel esperado de los alumnos como en el nivel de la investigación actual. Podremos considerar un doble cuestionamiento relativo a su impacto:
-
En primer lugar, ¿qué potencialidades ofrecen estos ambientes para transformar el trabajo matemático del alumno? Como consecuencia de la inclusión de diversas génesis, es conveniente ir más allá del enfoque instrumental para responder a esta pregunta.
-
La segunda cuestión consiste en estudiar en qué medida la utilización de entornos tecnológicos influye en la construcción epistemológica del alumno, que guía su trabajo matemático. Ello puede concernir, a título indicativo, tanto a la naturaleza de los objetos matemáticos que él construye, como a las pruebas matemáticas aceptables, así como su papel como medio de investigación.
Para expresar este interrogante en el marco particular de la geometría en ambientes tecnológicos, Coutat y Richard (2011) propusieron caracterizar los planos verticales del ETG idóneo, apoyándose en la idea de procesos: validación, modelización y descubrimiento (Fig. 4). En lo que concierne a la estructuración del ETM propuesto arriba (Fig. 3), estos procesos constituyen las manifestaciones de las competencias matemáticas del sujeto en el momento de su trabajo geométrico.
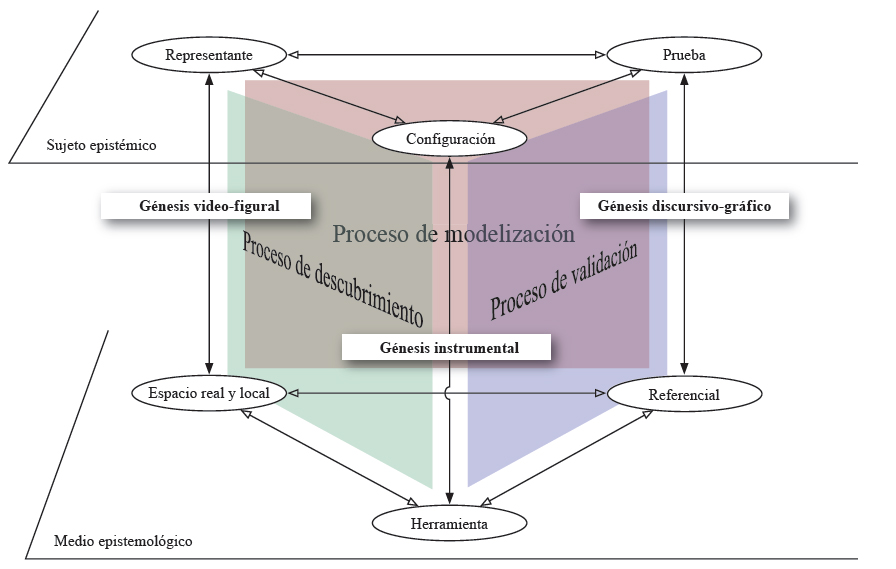
Figura 4
Los planos verticales en el ETG idóneo
Tema 3 - El trabajo matemático y los aspectos sociales e institucionales
De manera intrínseca, la cuestión de los contextos es central en la constitución del trabajo matemático. Se puede tratar como un enfoque interno para caracterizar dos facetas del trabajo de investigación del matemático con los contextos de descubrimiento y de justificación. A los contextos precedentes, podemos añadir el contexto de uso de las matemáticas que, con frecuencia, es el contexto principal para los alumnos y los usuarios habituales de las matemáticas, quienes se interesan generalmente en éstas debido a la potencia de sus aplicaciones. De la misma manera, es posible expandir la mirada sobre el trabajo matemático observando el rol de las instituciones particulares en las que este trabajo se inserta, junto al funcionamiento de las interacciones sociales y de lenguaje. El papel de la formación, inicial o continuada, de los profesores de matemáticas, aparece ya como una palanca institucional fundamental.
Tema 4 - Visualización y representación en el trabajo matemático
Debido a la variedad de los gráficos utilizados en todos los ámbitos de las matemáticas, la cuestión de la visualización y de su rol en el trabajo matemático se plantea inevitablemente. Si la visualización ha sido objeto de numerosos trabajos en geometría, son escasas las investigaciones que abordan la visualización en ámbitos matemáticos, aunque varias publicaciones contemporáneas subrayan su importancia (Guzmán, 1996, Alsina & Nelsen, 2006). Este tema se interesa por los conceptos de flexibilidad, de la génesis de los registros de representación semiótica y, de forma más amplia, el lugar de estos registros en el trabajo matemático, tradicional o instrumental - informático.
Spaces for Mathematical Work: Viewpoints and perspectives
1. A didactic perspective on mathematical work
The teaching of mathematics has been subject to a profound and worldwidere-examination since the beginning of the 1960s. Before this period the citizens of developed countries were offered two types of teaching by the school systems. The children with working class background were offered a brief and essentially utilitarian training in elementary mathematics. The children of the bourgeoisie, whose destiny was to take the economy and the governing of the country into their own hands, were given the opportunity to have access to a teaching of mathematics that was regarded as schooling in logical reasoning. In both cases, the student was placed in the position of a recipient of knowledge dispensed by the teachers. Starting from the 1960s, various phenomena have contributed to a change in the views on the role and the way of teaching of mathematics. Without pretending to be exhaustive, one can mention the reform of modern mathematics, the development of the researchon the learning experience of children, or also, the massification of the education in a context of economic and ideological competition.
For the purpose of our discussion, we will retain two profound characteristics of the changes which have become accentuated since: on the one hand, bringing to light the diversity of the work of the mathematician, viewed as the main actor in the advance of mathematics, and on the other hand, the pedagogical idea of stimulating the student’s activity in order to enhance the student’s ability to develop his or her knowledge in a problem-solving context. In each case, the mathematical work is in the core of the evolution, which leads logically to placing this concept centre stage in the didactics of mathematics.
The work we are referring to is a rational activity that is oriented towards a specific goal and is able to rely or not on the use of a certain number of specific instruments and artefacts. In mathematics, the purpose of this activity must be centred on the objects studied by the mathematicians, “these human beings working to advance the human understanding of mathematics” (Thurston, 1994, p. 162). Therefore, we consider that the didactic research should be concentrated on this double point of view – the learning experience of the students and the organization of this learning experience by the teacher within the context of a schooling that favours the development of the mathematical work of the student.
2. The Space for Mathematical Work concept
The general Space for Mathematical Work concept (ETM) expands the work space concept in geometry, introduced by Kuzniak and Houdement (Kuzniak, 2006) in the study of the didactics in this area. It was developed in order to help for better understand the didactical challenges around the mathematical work in a school environment. The space, conceived in this way, designs a well-thought and organized environment in order to permit the work of the individual solving mathematical problems. In the case of school mathematics, these individuals, generally, are not experts but pupils or students, either experienced or beginners.
From the specifi c study of geometry we retain the principle for articulation of two levels in the ETM (Kuzniak, 2011): the fi rst one of epistemological nature, in a close relation with the mathematical content of the studied area, and the other of cognitive nature, related to the thinking of the person solving mathematical tasks.
Therefore, the mathematical work is derived from a process which permits to impart, on the one hand, progressively gives a meaning to each of the epistemological and cognitive levels and, on the other hand, formulates these two levels thanks to different geneses. In the case of geometry, the entire process could be described as proceeding from the elements of the following diagram (Fig. 1), but it would need certain modifications in order to adapt it to the general framework of the ETM:
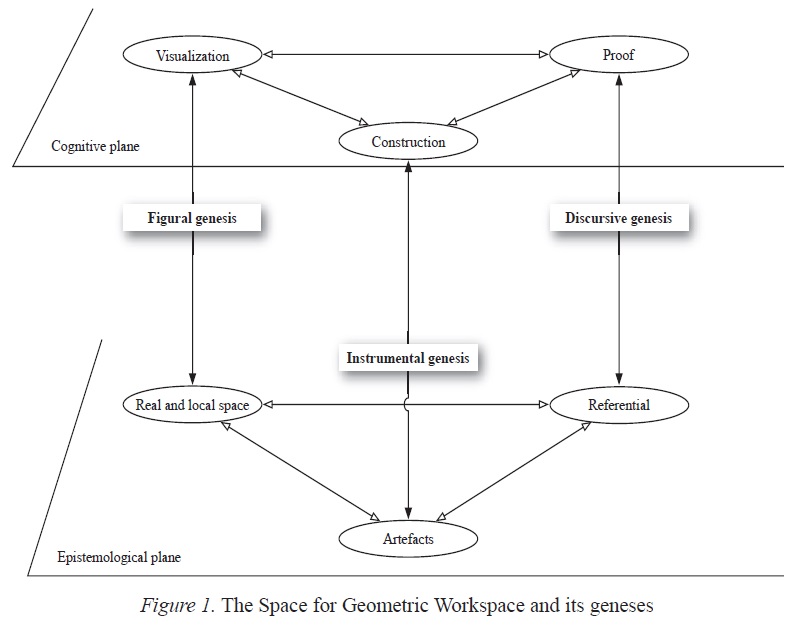
Figure 1
The Space for Geometric Workspace and its geneses
2.1 The epistemological level and its components
As regards the geometry, three components in interaction are characteristic for the geometric activity in its purely mathematical dimension:
-
a real and local space as support material, with one set of concrete and tangibles objects;
-
a set of artefacts such as drawing instruments or software;
-
a theoretical reference system based on definitions and properties.
These components are not juxtaposed; they must be organized according to a predetermined goal which will depend on the mathematical domain in its epistemological dimension. While the emphasis is on the process of the learning of the student in a didactic situation, this epistemological plan can be considered also as an epistemological environment (Coutat & Richard, 2011).
If the artefacts and theoretical referential remain two basic components of any epistemological plan associated with a specific mathematical domain, the component linked to the space and to the geometrical configurations must be modified in order to be expanded to other mathematical domains. In accordance with one concept of the mathematics based on semiotic representations, which goes beyond the single consideration of systems of representation, it seems pertinent to use the term sign or representamen in the sense of Peirce. Therefore, the sign or the representamen is “something” which represents something else that can be its object or maybe also itself as such. Following the respective mathematical domain, the signs can be geometrical images, algebraic symbols or graphics and even tokens; they can also be models or photos in the case of problems that involve modelling. Unlike the signs with dyadic structure, which retain only the relation of reference between the signifi er and the represented object, the idea of a sign, which is also its own representation, invites to revisiting the semiotic process when the mathematical work is at stake. This is particularly visible when a geometrical image, which is a form in itself, is at the same time representamen and model of representation (Coutat, Laborde & Richard, 2016).
2.2 The cognitive process level
The mathematics that is taught is not a disembodied set of properties and objects reduced to signifi ers that can be manipulated by formal systems – it is fi rst of all and mainly a human activity. Therefore, it is essential to understand how communities of individuals, but also specifi c individuals, use and internalize the mathematical knowledge in their practice of the discipline. It is also essential to understand how they will impart a meaning to all these tangible signs and objects. This implies a second level of the ETM centred on the subject which is viewed as a cognitive subject. This introduction to the cognitive fi eld must be made in close relation to the components of the epistemological level and, in order to remain within the didactical framework, it is possible to adapt the semiotic approach of Duval (1995, 2005). For the geometrical activity, these processes are as follows:
-
a process of visualization related to the representation of the space and the support material;
-
a process of construction and function of the used instruments (rulers, compass, etc.) and the respective geometrical configurations;
-
a discursive process producing arguments and proves.
The process of visualization needs to be specified precisely in order to find its place in an extension to the ETM. It must be associated with the diagrams and operations of the use of the signs, about which nothing proves a priori that they all pick up the entire visualization as such, even within its extended conceptualization (Fig.2).
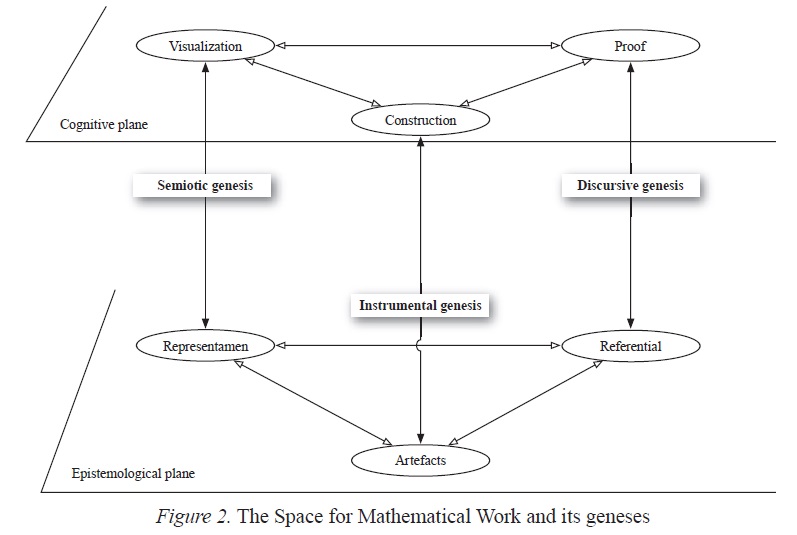
Figure 2
The Space for Mathematical Work and its geneses
This process of “extended” visualization has to be well distinguished from the simple vision or perception of the objects; it can be envisaged as a process of structuring the information provided by the diagrams and the signs. It nourishes the intuition of the properties and sometimes contributes to establishing cognitively the validity of these properties. Under certain conditions, it can be likened to a reasoning of a discursive-graphical type (Richard, 2004) and can be expressed in the interior of the registers of a determined semiotic representation.
3. The reference, adequate and personal ETM
Within the theoretical framework of ETM, just as within that of Space for Geometrical Work (ETG), the paradigm concept orients and structures the organization of the components wich, due to their different functions, participate in the specifics of the different paradigms at play. A paradigm is instituted when a given community of individuals agree to formulate problems and organize their solutions by prioritizing certain tools or certain forms of thinking. The "paradigmatic" workspace, such as it is defined by this community, will be called a reference ETM. In a given educational institution, the solving of a problem assumes that an adequate ETM could be organized in order to permit a student to participate in the solving of the problem. This adequate ETM must necessarily fulfil two conditions: on the one hand, to permit work in the paradigm that corresponds to the problems in question; on the other hand, to be “well designed” in the sense that its different components are organized in a valid manner. Its designer plays a role here that is similar to that of the architect who designs a workspace for the potential users. In the classroom, the design of this space will depend on the personal ETM of the teacher. When the problem is assigned to a student, its mathematical treatment by the student will take place within the personal ETM of this student. Based on this fact, the adequate ETM is not fixed and has to be continuously modified in order to adjust itself to the local constraints.
Therefore, the mathematical work within school settings can be described at three ETM levels: the mathematics as seen by the institution is described in the reference ETM; it must be converted by the teacher into adequate ETM to permit its effective implementation in class where everyone will work in his/her personal ETM; the choice and organization of the tasks given by the teacher to the students are essential in the constitution of the adequate ETM, so that the teacher gives an opportunity to the students to solve in an adequate manner the questions offered, i.e. in a way that is in conformity with the institutional expectations that are described more or less explicitly in the reference ETM. These choices and the management of the activities will depend, to a large extent, on the personal ETM of the teacher. The observation of the activity of the students will permit them to identify their personal ETMs by identifying eventual sub-assemblies of stable practices in them.
4. The geneses of the work in the ETM
The development by an individual of his or her mathematical work takes place gradually and passes through a gradual approach to the implementation of his or her personal ETM. This global genesis of the ETM supposes the use of a set of geneses which are interdependent and concern all epistemological components and the cognitive processes. The activation and the control of these geneses can be initiated by the teacher (at the level of the adequate ETM). It is important to know to what extent they are in conformity upstream with the expectations defi ned in the reference ETM (Kuzniak & Rauscher, 2011; Kuzniak, 2013).
As we see it, the epistemological and cognitive plans structure the ETM in two levels and help to understand the circulation of the knowledge within the mathematical work. How then, proceeding from here, should we formulate the epistemological and cognitive levels, in an operative manner, so that it is possible for the expected mathematical to work? We think that it is appropriate to use the three fundamental geneses as a base of the theoretical framework developed above:
-
The Instrumental genesis, which allows us to make the artefacts operational in the constructive process contributing to the accomplishment of the mathematical work;
-
The semiotic genesis based namely on the registers of the semiotic representation which gives meaning to the ETM objects and confers to them their status of operative mathematical objects. In this way, this semiotic genesis ensures the relationships between syntax, semantics, function and structure of the conveyed signs;
-
The discursive genesis of the proof used by the properties combined together in the theoretical referential in order to put them in service to the mathematical reasoning and to a non-exclusively iconic, graphic or instrumented validation.
In order to define the geometrical work within the framework of the ETG, Coutat and Richard (2011) describe the interactions that are specific to the geometrical approach (see Fig. 4) by characterizing the three vertical plans which appear naturally in the diagram of the ETG. In our effort to provide a theoretical construct of an ETM by generalizing the achievements of the research on the ETGs, the vertical plans introduced in this way can be related to different phases of the mathematical work implemented within the execution of a given task: discovery and exploration, justification and reasoning, presentation and communication. The effective realization of these phases will define de facto a certain number of cognitive mathematical competences based on the coordination of the geneses in their relations with the epistemological plan (Fig. 3).
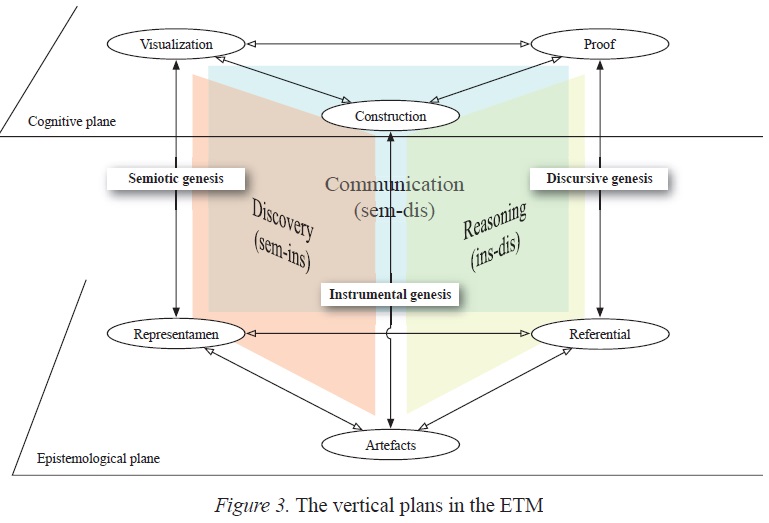
Figure 3
The vertical plans in the ETM
A first type of interaction favours the identification and exploration of objects on the basis of the semiotic and instrumental geneses in order to develop a competence related to the discovery of a solution of the mathematical problems. A second type of interaction develops the mathematical reasoning on the basis of justification of the discoveries and formulating the instrumental and discursive geneses. And finally, one last type is oriented towards the mathematical communication of the results and is based essentially on the semiotic and discursive geneses. The exact definition of these plans of interactions and the description of their interrelations depend on the specific mathematical domain that is studied
5. About the themes of this special issue
The articles in this issue are centred on the mathematical work and it constitutes the scientifi c core around which the cohesion of the scientifi c community was formed during the symposium. Without limiting themselves to the elaboration of a Space for Mathematical Work in its technical sense, the object of the articles retained for the special issue is devoted on a wider scale to the study of the semiotic, cognitive and instrumental dimensions of the mathematical work without excluding a priori any epistemological or didactic approaches. This expansion of the problematic to include the entire mathematical work in its different forms has been submitted to the wisdom of the contributors starting with four subjects for refl ection, which can be found in the present issue.
Theme 1 – The mathematical work and the ETM
The object of this theme is, on the one hand, to go deeper into the theoretical model defined by the Space for Mathematical Works and, on the other hand, to explore their use as analytical tool in specific studies. The use of this model in other domains than geometry supposes a specific and targeted study of the areas in question and suggests thinking about ETMs which, as in the geometry, can be applied to the algebra, the analysis, the arithmetic… In order to harmonize the notations, these specific workspaces, associated to the specific domains d,will be notated as ETMd, i.e. ETMalgebra, ETManalysis, ETMarithmetic, … The Space for Mathematical Work can be viewed as a network of diverse fibres constituting theETMd. Therefore, the issue is knowing how the links between the spaces or the browsing of the plans are organized. These interactions between the domains are essential for understanding the global functioning of the mathematical work and, in addition, they require taking into consideration the processes of modelling within the framework of the ETMs, besides the purely semiotic issues.
Theme 2 – Technological environments and mathematical work
This theme is interested specifically in the use of technological environments not for themselves, but to specify to what extent they affect the mathematical work. In fact, the emergence of many new contemporary instruments has contributed to the formation of a new relief of the constructive aspects and the artefacts supporting the execution of the mathematical work both at the level expected by the students and the level of the current research. We can consider their impact twice.
-
In the first place, what are the potentials of such environments for transforming the mathematical work of the student? By taking into consideration the diverse geneses, it is advantageous to move out of the instrumental approach in order to answer this question.
-
The second question requires studying in what aspects the use of technological environments infl uences the epistemological formation of the student, guiding his/her mathematical work. This can concern, for illustrative purposes only, the nature of the mathematical objects constructed and the acceptable mathematical proofs, as well as its role as a research instrument
In order to answer this issue within the specific framework of geometry in the technological environments, Coutat and Richard (2011) have proposed to characterize the vertical plans of the adequate ETG by basing them on the approach idea: validation, modelling and discovery (Fig. 4). As regards the structuring of the ETM proposed above (Fig. 3), these approaches constitute the manifestations of the mathematical competences of the subject in the course of the geometrical work
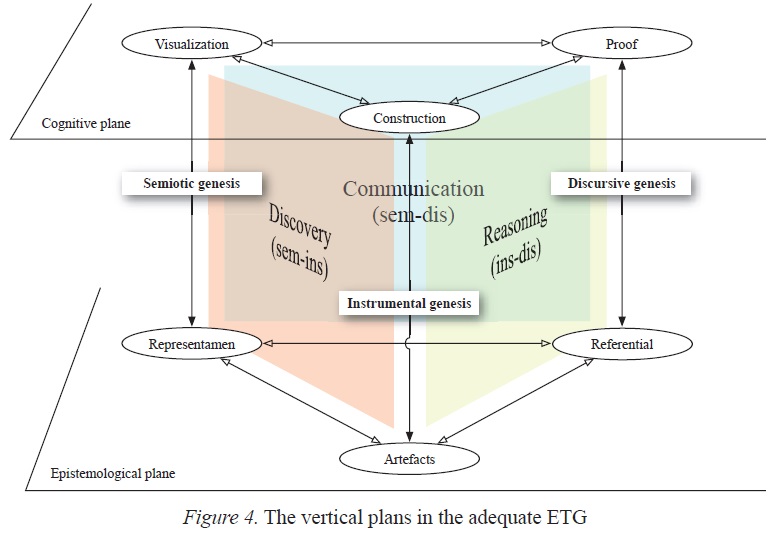
Figura 4
The vertical plans in the adequate ETG
Theme 3 – The mathematical work and its social and institutional aspects
Intrinsically, the question of the contexts is central in the constitution of the mathematical work. It can be about an internal approach in order to characterize two facets of the research work of the mathematician with the discovery and justifi cation contexts. The context of use of the mathematics can be added to the preceding contexts, which is often the main context for the students and the regular users, who are generally interested in it because of the power of its applications. It is also possible to expand the view on the mathematical work by observing the role of the specifi c institutions, into which this work is inserted, along with the play of the social and linguistic interactions. The role of the education, the initial or continuous one, and of the mathematic teachers appears here as a fundamental institutional lever.
Theme 4 – Visualization and representation in the mathematical work
From the fact of the variety of the graphical representations used in all domains of mathematics, the question about the visualization and its global role in the mathematical work inevitably arises. While the visualization has been object of numerous research investigations in geometry, there are much fewer investigations on the visualization in other areas of mathematics, although many contemporary publications emphasize their importance (Guzmán, 1996; Alsina & Nelsen, 2006). This theme is interested in the topics of flexibility, in the genesis of the semiotic representation registers and, more generally, in the place of these registers in the mathematical work, traditional or instrumented.
Espaces de travail mathématique. Points de vue et perspectives
1. Une perspective didactique sur le travail mathématique
L'enseignement des mathématiques a connu une profonde remise en question à partir des années soixante et ceci dans le monde entier. Avant cette période, les systèmes scolaires offraient deux types d’enseignement aux citoyens des pays développés. Aux enfants des milieux populaires était proposé un enseignement court et essentiellement utilitariste des mathématiques élémentaires. Les enfants de la bourgeoisie, destinés à prendre en main l’économie et la gestion du pays, avaient la possibilité d’accéder à un enseignement des mathématiques vues comme une école du raisonnement logique. Dans les deux cas, l'élève était placé en position de recépteur d'un savoir dispensé par des maîtres. Á partir des années soixante, divers phénomènes ont contribué à changer les points de vue sur le rôle des mathématiques et sur la façon de les enseigner. Sans viser à l'exhaustivité, on peut signaler la réforme des mathématiques modernes, le développement des recherces sur les apprentissages des enfants ou encore, la massification de l'enseignement dans un contexte de concurrence économique et idélogique.
Pour notre propos, nous retiendrons deux profondes caractéristiques des changements qui se sont accentués depuis : d’une part, la mise en évidence de la diversité du travail du mathématicien vu comme l’acteur principal de la progression mathématique et, d’autre part, l’idée pédagogique depromouvoir l’activité de l’élève pour le rendre plus apte à développer ses connaissances dans un contexte de résolution de problèmes. Dans chaque cas, le travail mathématique est au cœur de l’évolution, ce qui conduit logiquement à donner à cette notion une place centrale en didactique des mathématiques.
Le travail auquel nous nous référons porte sur une activité rationnelle orientée vers un but particulier et pouvant s’appuyer ou non sur l’usage d’un certain nombre d’instruments et d’artéfacts spécifi ques. En mathématiques, le but de cette activité sera centré sur les objets étudiés par les mathématiciens, « ces êtres humains qui font avancer la compréhension humaine des mathématiques » (Thurston, 1994, p. 162). Nous considérons alors que la recherche didactique doit s’interroger sur ce travail du double point de vue de l’apprentissage par les élèves et de l’organisation de cet apprentissage par le professeur, dans le cadre d’un enseignement favorisant le développement du travail mathématique de l’élève.
2. La notion d’Espace de Travail Mathématique
La notion générale d’Espace de Travail Mathématique (ETM) étend la notion d’espace de travail pour la géométrie, introduite par Kuzniak et Houdement (Kuzniak, 2006) dans l’étude de la didactique de ce domaine. Elle a été mise au point afin d’aider à mieux comprendre les enjeux didactiques autour du travail mathématique dans un cadre scolaire. L’espace ainsi conçu désigne un environnement pensé et organisé pour permettre le travail des individus résolvant des problèmes mathématiques. Dans le cas des mathématiques scolaires, ces individus ne seront généralement pas des experts, mais des élèves ou étudiants, confi rmés ou débutants.
De l’étude particulière de la géométrie, nous retenons le principe d’articuler dans l’ETM deux niveaux (Kuzniak, 2011), l’un de nature épistémologique, en rapport étroit avec les contenus mathématiques du domaine étudié, et l’autre, de nature cognitive, qui concerne la pensée du sujet résolvant des tâches mathématiques.
Le travail mathématique résulte alors d’un processus qui va permettre de donner progressivement un sens, d’une part, à chacun des niveaux épistémologique et cognitif et, d’autre part, d’articuler ces deux niveaux grâce à différentes genèses. Dans le cas de la géométrie, l’ensemble du processus a pu être décrit à partir des éléments du diagramme suivant (Fig. 1), mais celui-ci nécessitera certaines modifi cations pour l’adapter au cadre général des ETM :
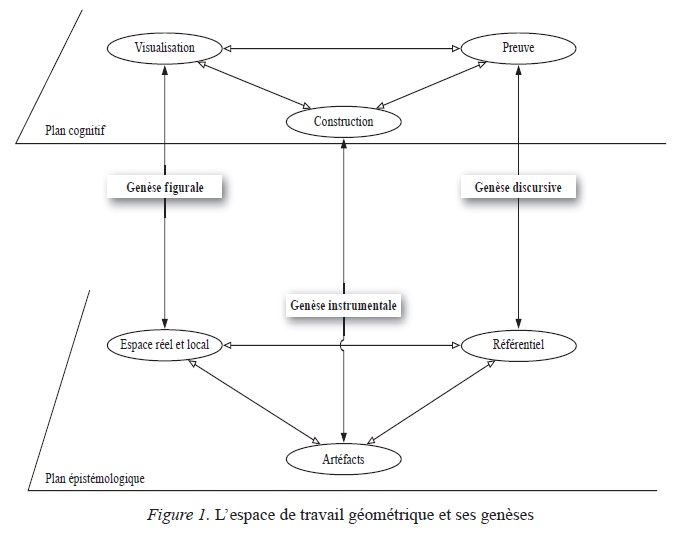
Figure 1
L'espace de travail géometrique et ses genèses
2.1 Le niveau épistémologique et ses composantes
En ce qui concerne la géométrie, trois composantes en interaction sont caractéristiques de l’activité géométrique dans sa dimension purement mathématique :
-
un espace réel et local comme support matériel, avec un ensemble d’objets concrets et tangibles ;
-
un ensemble d’artéfacts tels que des instruments de dessin ou des logiciels ;
-
un système théorique de référence basé sur des définitions et des propriétés.
Ces composantes ne sont pas juxtaposées, elles doivent être organisées selon un but déterminé qui va dépendre du domaine mathématique dans sa dimension épistémologique. Lorsque l’accent est mis sur le processus d’apprentissage de l’élève dans une situation didactique, ce plan épistémologique peut aussi se considérer comme un milieu épistémologique (Coutat & Richard, 2011).
Si les artéfacts et le référentiel théorique restent deux composantes de base de tout plan épistémologique associé à un domaine mathématique particulier, la composante liée à l’espace et aux configurations géométriques doit être modifiée pour l’étendre à d’autres domaines mathématiques. En accord avec une conception des mathématiques fondées sur des représentations sémiotiques qui va au-delà de la seule considération de systèmes de représentation, il semble pertinent d’utiliser la notion de signe ou representamen, au sens de Peirce. Ainsi, le signe ou le representamen est une « chose » qui en représente une autre que ce soit son objet ou peut-être aussi lui-même. Suivant le domaine mathématique concerné, les signes pourront être des dessins géométriques, des symboles algébriques ou des graphiques, voire des jetons,des maquettes ou des photos dans le cas de problèmes qui mettent en jeu de la modélisation. À la différence des signes de structure dyadique qui ne retiennent que la relation de référence entre le signifiant et l’objet représenté, l’idée d’unsigne qui est aussi sa propre représentation invite à revisiter le processus sémiotique lorsque le travail mathématique est en jeu. Ceci est notamment visible lorsqu’un dessin géométrique, qui est lui-même une forme, est à la fois representamen et modèle de représentation (Coutat, Laborde & Richard, 2016).
2.2 Le niveau des processus cognitifs
La mathématique enseignée n’est pas un corpus désincarné de propriétés et d’objets réduits à des signifiants manipulables par des systèmes formels, elle est d’abord et principalement une activité humaine. Ainsi, il est essentiel de comprendre comment des communautés d’individus, mais aussi des individus particuliers, utilisent et s’approprient les connaissances mathématiques dans leur pratique de la discipline. Il est aussi essentiel de comprendre comment ils vont donner un sens à tous ces signes et objets tangibles. Cela implique un deuxième niveau de l’ETM centré sur le sujet vu comme un sujet cognitif. Cette ouverture sur le champ cognitif doit se faire en étroite relation avec les composantes du niveau épistémologique et, pour rester dans un cadre didactique, il est possible d’adapter l’approche sémiotique de Duval (1995, 2005). Pour l’activité géométrique, ces processus sont :
-
un processus de visualisation relatif à la représentation de l’espace et au support matériel ;
-
un processus de construction, fonction des instruments utilisés (règles, compas, etc.) et des configurations géométriques en jeu ;
-
un processus discursif, qui produit des argumentations et des preuves.
Le processus de visualisation nécessite d’être précisé pour trouver sa place dans une extension aux ETM. Il doit être associé à des schèmes et des opérations d’usage des signes dont rien ne prouve a priori qu’ils relèvent tous de la visualisation en tant que telle, même dans une conception étendue de celle-ci (Fig.2).
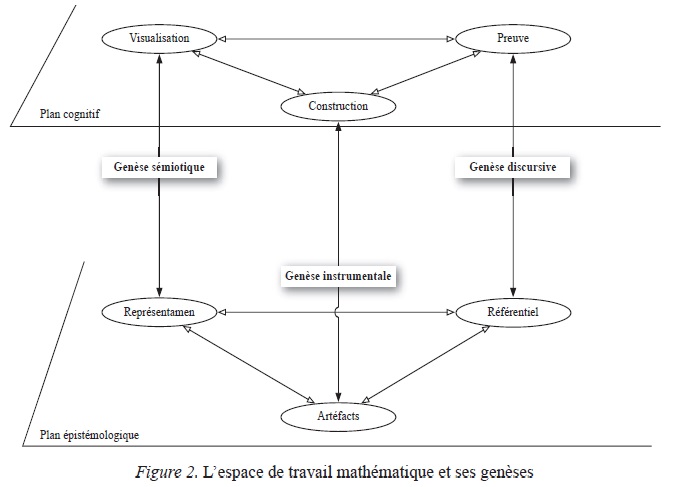
Figure 2
L'espace de travail mathématique et ses genèses
Ce processus de visualisation « étendue » doit bien être distingué de la simple vision ou perception des objets, il peut être envisagé comme le processus de structuration des informations apportées par les diagrammes et les signes. Il nourrit l’intuition des propriétés et il contribue parfois à fonder cognitivement la validité de ces propriétés. Sous certaines conditions, il peut s’apparenter à un raisonnement de type discursivo-graphique (Richard, 2004) et pourra s’exprimer à l'intérieur de registres de représentation sémiotique déterminés.
3. Les ETM de référence, idoines et personnels
Dans le cadre théorique des ETM tout comme dans celui des Espaces de Travail Géométrique (ETG), la notion de paradigme oriente et structure l’organisation des composantes qui, par leurs fonctions différentes, participent à laspécificité des divers paradigmes en jeu. Un paradigme s’institue quand une communauté d’individus s’accorde pour formuler des problèmes et organiser leurs solutions en privilégiant certains outils ou certaines formes de pensée. L’espace de travail «paradigmatique» tel qu’il est alors défini par cette communauté sera appelé ETM de référence. Dans une institution scolaire donnée,la résolution d’un problème suppose qu’un ETM idoine a pu être organisé pour permettre à un élève de s’engager dans la résolution du problème. Cet ETM idoine doit nécessairement remplir deux conditions: d’une part permettre detravailler dans le paradigme correspondant à la problématique visée, d’autre partêtre « bien construit », dans le sens où ses différentes composantes sont organisées de manière valide. Son concepteur joue ici un rôle semblable à celui del’architecte qui conçoit un espace de travail pour des utilisateurs potentiels.En classe, la conception de cet espace va dépendre de l’ETM personnel du professeur. Lorsque le problème est proposé à un élève, son traitement mathématique par l’élève va être conduit dans l’ETM personnel de cet élève. De ce fait, l’ETM idoine n’est pas figé et il doit sans cesse être modifié pour s’ajuster aux contraintes locales.
Ainsi, le travail mathématique dans un cadre scolaire pourra être décrit grâce à trois niveaux d’ETM : la mathématique visée par l’institution est décrite dans l’ETM de référence. Celui-ci doit être aménagé par le professeur en ETM idoine pour permettre une mise en place effective dans les classes, où chaque élève travaillera dans son ETM personnel.
Le choix et l’organisation des tâches données aux élèves par leur professeur sont essentiels dans la constitution de l’ETM idoine, afin qu’il donne la possibilité aux élèves de résoudre de manière adéquate les questions proposées, c’est-à-dire de manière conforme aux attentes institutionnelles décrites de façon plus ou moins explicite dans l’ETM de référence. Ces choix et la gestion des activités vont dépendre en grande partie de l’ETM personnel du professeur. L’observation de l’activité des élèves permettra d’identifi er leurs ETM personnels en y repérant d’éventuels sous-ensembles de pratiques stables.
4. Les genèses à l’œuvre dans les ETM
La développement par un individu de son travail mathématique s'opère graduallement et passe para la mise en place progressive de son ETM personnel. Cette genèse globale de l’ETM suppose un ensemble de genèses qui sont interdépendantes et qui concernent toutes les composantes épistémologiques et les processus cognitifs. L’activation et le contrôle de ces genèses peuvent être initiés par les enseignants (au niveau de l’ETM idoine). Il importe de savoir dans quelle mesure, elles sont conformes, en amont, aux attentes défi nies dans l’ETM de référence (Kuzniak & Rauscher, 2011 ; Kuzniak, 2013)
Comme nous l’avons vu, les plans épistémologique et cognitif structurent les ETM en deux niveaux et ils aident à comprendre la circulation des connaissances au sein du travail mathématique. Comment dès lors articuler de façon opératoire les niveaux épistémologiques et cognitifs afin de rendre possible le travail mathématique attendu ? Il nous apparaît convenable de s’appuyer sur les trois genèses fondamentales issues du cadre théorique développé plus haut:
-
Une genèse instrumentale qui permet de rendre opératoire les artéfacts dans le processus constructif qui contribue à l’accomplissement du travail mathématique ;
-
une genèse sémiotique basée notamment sur les registres de représentation sémiotique, qui donne un sens aux objets de l’ETM et leur confère leur statut d’objets mathématiques opératoires ;
-
cette genèse sémiotique assure ainsi la mise en relation entre syntaxe, sémantique, fonction et structure des signes véhiculés ;
-
une genèse discursive de la preuve qui utilise les propriétés réunies dans le référentiel théorique pour les mettre au service du raisonnement mathématique et d’une validation non exclusivement iconique, graphique ou instrumentée.
Afin de définir le travail géométrique dans le cadre des ETG, Coutat et Richard (2011) décrivent les interactions spécifiques à la démarche géométrique (voir Fig. 4) en caractérisant les trois plans verticaux qui apparaissent naturellement dans le diagramme des ETG. Dans notre effort de construction théorique des ETM généralisant les acquis de la recherche sur les ETG, les plans verticaux ainsi introduits vont pouvoir être reliés aux différentes phases du travail mathématique mis en œuvre dans l’exécution d’une tâche : découverte et exploration, justification et raisonnement, présentation et communication. La réalisation effective de ces phases définira, de fait, un certain nombre de compétences mathématiques cognitives fondées sur la coordination des genèses dans leurs relations avec le plan épistémologique (Fig. 3).
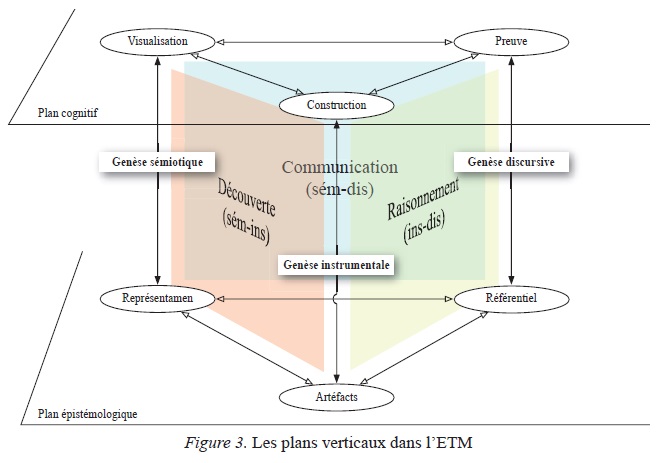
Figure 3
Les plans verticaux dans l'ETM
Un premier type d’interactions (Sem-Ins) privilégie l’identification et l’exploration des objets en s’appuyant sur les genèses sémiotique et instrumentale pour développer une compétence liée à la découverte de la solution de problèmes mathématiques. Un second type d’interactions (Ins-Dis) développe le raisonnement mathématique fondé sur la justification des découvertes en articulant les genèses instrumentale et discursive. Enfin, un dernier type (Sem-Dis) est orienté vers la communication mathématique des résultats et il s’appuiera essentiellement sur les genèses sémiotique et discursive. La défi nition exacte de ces plans d’interactions et la description de leurs interrelations dépend du domaine mathématique spécifi que étudié
5. Sur les thèmes de ce numéro spécial
Le travail mathématique fédère l’ensemble des contributions à ce numéro et il constitue le cœur scientifi que autour duquel s’est constituée la cohésion de la communauté scientifi que lors des symposiums. Sans se restreindre à l’élaboration d’un Espace de Travail Mathématique dans son sens technique, l’objet des communications retenues pour le numéro spécial vise plus largement à s’interroger sur les dimensions sémiotiques, cognitives et instrumentales du travail mathématique en n’excluant a priori aucune approche épistémologique ou didactique. Cet élargissement de la problématique à tout le travail mathématique sous ses différentes formes avait été soumis à la sagacité des contributeurs à partir de quatre thèmes de réfl exion que l’on retrouve dans le présent numéro.
Thème 1 – Le travail mathématique et les ETM
L’objet de ce thème est, d’une part, d’approfondir le modèle théorique défini par les Espaces de Travail Mathématique et, d’autre part, d’en explorer les utilisations comme outil d’analyse dans des études particulières. Utiliser ce modèle dans d’autres domaines que celui de la géométrie suppose une étude particulière et ciblée des domaines en question et amène à penser des ETM qui, comme en géométrie, peuvent s’appliquer à l’algèbre, à l’analyse, à l’arithmétique… Pour harmoniser les notations, ces espaces de travail spécifiques, associés à des domaines d particuliers, seront notés ETMd, c’est-à-dire des ETMalgèbre, ETManalyse, ETMarithmétique , … L’Espace de Travail Mathématique peutêtre vu comme une mise en réseau des diverses fibres que constituent les ETMd.La question se pose alors de savoir comment s’organisent la fibration entre espaces ou le feuilletage des plans. Ces interactions entre les domaines sont essentielles pour comprendre le fonctionnement global du travail mathématique et elles forcent en outre la considération des processus de modélisation dans le cadre des ETM, au-delà des seules questions sémiotiques.
Thème 2 – Environnements technologiques et travail mathématique
Ce thème s'intéresse spécifiquement à l'utilisation d'environnements technologiques, non pour eux-mêmes, mais pour préciser dans quelle mesure ils affectent le travail mathématique. De fait, l’apparition contemporaine de nombreux instruments a contribué à donner un relief nouveau aux aspects constructifs et aux artéfacts qui soutiennent l’exécution du travail mathématique, tant au niveau attendu des élèves qu’au niveau de la recherche actuelle. On pourra retenir une double interrogation relativement à leur impact :
-
En premier lieu, quelles potentialités offrent de tels environnements pour transformer le travail mathématique de l’élève ? Du fait de la prise en compte de diverses genèses, il reste avantageux de dépasser la seule approche instrumentale pour répondre à cette question.
-
L seconde interrogation consiste à étudier en quoi l'utilisation d'environnements technologiques influence la construction épistémologique de l’élève, guidant son travail mathématique. Cela peut concerner, à titre indicatif, aussi bien la nature des objets mathématiques qu’il construit que les preuves mathématiquement acceptables, de même que son rôle en tant que moyen d’investigation.
Pour exprimer cette interrogation dans le cadre particulier de la géométrie dans des environnements technologique, Coutat et Richard (2011) ont proposé de caractériser les plans verticaux de l’ETG idoine en s’appuyant sur l’idée de démarches : validation, modélisation et découverte (Fig. 4). Au regard de la structuration de l’ETM proposé plus haut (Fig. 3), ces démarches constituent les manifestations des compétences mathématiques du sujet lors de son travail géométrique.
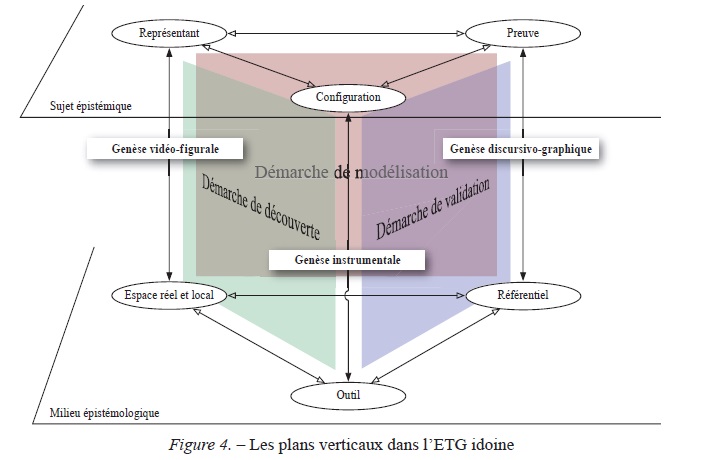
Figure 4
Les plans verticaux dans l'ETG idoine
Thème 3 – Le travail mathématique et les aspects sociaux et institutionnels
De manière intrinsèque, la question des contextes est centrale dans la constitution du travail mathématique. Il peut s’agir d’une approche interne pour caractériser deux facettes du travail de recherche du mathématicien avec les contextes de découverte et de justification. Aux contextes précédents, on peut ajouter le contexte d’usage des mathématiques qui, souvent, est le contexte principal pour les élèves et les utilisateurs usuels des mathématiques, qui s’intéressent généralement à celles-ci pour la puissance de ses applications. Il est également possible d’élargir le regard sur le travail mathématique en observant le rôle des institutions particulières dans lesquelles ce travail s’insère, conjointement au jeu des interactions sociales et langagières. Le rôle de formation, initiale ou continue, des enseignants en mathématiques apparaît ici comme un levier institutionnel fondamental.
Thème 4 – Visualisation et représentation dans le travail mathématique
Du fait de la variété des représentations graphiques utilisées dans tous les domaines mathématiques, la question de la visualisation et de son rôle global dans le travail mathématique se pose inévitablement. Si la visualisation a fait l’objet de nombreux travaux en géométrie, beaucoup moins de recherches concernent la visualisation dans d’autres domaines mathématiques, encore que plusieurs publications contemporaines en soulignent l’importance (Guzmán, 1996 ; Alsina & Nelsen, 2006). Ce thème s’intéresse aux notions de fl exibilité, à la genèse des registres de représentation sémiotique et plus généralement, à la place de ces registres dans le travail mathématique, traditionnel ou instrumenté.
Referencias
Alsina, C. & Nelsen, R. (2006). Math Made Visual: Creating Images for Understanding Mathematics. Estados Unidos: The Mathematical Association of America.
Coutat, S. & Richard, P. R. (2011). Les figures dynamiques dans un espace de travail mathématique pour l’apprentissage des propriétés géométriques. Annales de didactique et de sciences cognitives, 16, 97-126.
Coutat, S., Laborde, C. & Richard, P. R. (2016). L’apprentissage instrumenté de propriétés en géométrie : propédeutique à l’acquisition d’une compétence de démonstration. Educational Studies in Mathematics, 93 (2), 195-221
Duval, R. (1995). Why to teach geometry. ICMI Study on Geometry, (53-58) Catania.
Duval, R. (2005). Les conditions cognitives de l’apprentissage de la géométrie: Développement de la Visualisation, Différenciation des Raisonnements et Coordination de leurs Fonctionnements. Annales de Didactique et de sciences cognitives, 10, 5-53.
Guzmán, M. (1996). El Rincón de la Pizarra. Ensayos de Visualización en Análisis Matemático. Elementos Básicos del Análisis. Madrid, España: Ediciones Pirámide.
Kuzniak, A. (2006). Paradigmes et espaces de travail géométriques. Éléments d’un cadre théorique pour l’enseignement et la formation des enseignants en géométrie. Canadian Journal of Science and Mathematics Education, 6 (2) 167-187.
Kuzniak, A. (2011). L’espace de Travail Mathématique et ses genèses. [El espacio de trabajo matemático y su génesis] Annales de didactique et de sciences cognitives, 16, 9-24.
Kuzniak, A. (2013) Understanding the nature of the geometric work through its development and its transformations. In Rezat (ed) Transformation – A fundamental idea of Mathematics Education. (pp. 311-325). Springer.
Kuzniak, A. & Rauscher J. C. (2011). How do teachers’ approaches to geometric work relate to geometry students’ learning difficulties? Educational Studies in Mathematics, 77 (1), 129-147.
Richard, P. R. (2004). L’inférence figurale: Un pas de raisonnement discursivo - graphique. Educational studies in Mathematics, 57 (2), 229-263.
Thurston, W. P. (1994). On proof and progress in mathematics. Bulletin of American Mathematical Society, 30 (2). 161-177.
