Algoritmo aplicado en la sostenibilidad de una empresa de deportes
ALGORITHM APPLIED TO THE SUSTAINABILITY OF A SPORT COMPANY
Algoritmo aplicado en la sostenibilidad de una empresa de deportes
Revista Venezolana de Análisis de Coyuntura, vol. XXIV, núm. 1, pp. 135-153, 2018
Universidad Central de Venezuela
Recepción: 02 Octubre 2017
Aprobación: 11 Diciembre 2017
Resumen: Los stakeholders presentan un rol importante hacia la sostenibilidad de las empresas. Sin embargo, la priorización de temas relevantes no es una tarea sencilla para los tomadores de decisiones. Los empresarios demandan de herramientas que reducen los riesgos y los apoyen, tanto en la toma de decisiones como en la definición de sus estrategias. En este contexto, el artículo tiene como objetivos ampliar la discusión sobre sostenibilidad en las empresas y plantear soluciones para la toma de decisiones a partir de la lógica borrosa. Para conseguir este reto, se presenta un algoritmo de lógica borrosa aplicado en la priorización de temas relevantes en una empresa multinacional de deportes. Los resultados demuestran la utilidad de esta herramienta en los procesos de toma de decisiones en las empresas. Se considera también que este trabajo sea una contribución para promover la sostenibilidad en las empresas y futuros estudios de investigación sobre la toma de decisiones.
Palabras clave: Sostenibilidad, Stakeholders, Lógica borrosa, Deportes, Toma de decisión.
Abstract: Stakeholders play an important role in the sustainability of companies. However, prioritization of relevant issues is not a simple task for decision makers. Entrepreneurs demand tools that reduce risks and support them both in decision-making and in the definition of their strategies. In this context, the paper aims to broaden the discussion about sustainability in companies and propose solutions for decision making from the fuzzy logic. To achieve this challenge we present a fuzzy logic algorithm applied in the prioritization of relevant topics in a multinational sports company. The results demonstrate the utility of this tool in the decision making processes in companies. It is also considered that this work is a contribution to promote sustainability in companies and future research studies on decision making.
Keywords: Sustainability, Stakeholders, Fuzzy Logic, Sports, Decision Making.
Introducción
Diversos estudios científicos indican que la responsabilidad social empresarial (Bowen, 1953; Carroll, 1979; Wartick y Cochran, 1985; Lee, 2008; Freeman y col. 2010 y Porter y Kramer, 2011) y la sostenibilidad empresarial (Elkington, 1994-1999; Hart y Milstein, 2003 y Paula, 2011) han evolucionado en las últimas décadas en términos de conceptos, estrategias y aplicaciones hacia el desarrollo sostenible de las empresas.
Por otro lado, la Teoría de los Grupos de Interés, también conocido como Stakeholder Theory, postula que la capacidad de una empresa para generar una riqueza sostenible a lo largo del tiempo y, con ello, su valor a largo plazo, viene determinada por sus relaciones con sus grupos de interés (Freeman, 1984). Según el mismo autor, el grupo de interés de una empresa es (por definición) cualquier grupo o individuo que puede afectar o es afectado por el logro de los objetivos de la organización, como por ejemplo, sus clientes, colaboradores, proveedores, gobierno, comunidades, entre otros.
De acuerdo con Freeman y col. (2010), la responsabilidad social empresarial (RSE) debe estar integrada en toda la organización, de manera transversal y que involucre la participación de todas áreas de ésta. Por definición, la empresa debe buscar la integración de criterios económicos, éticos, sociales y ambientales y que todas las partes interesadas tengan una posición moral. De acuerdo con los mismos autores, la empresa responsable busca la creación de valor para sus stakeholders y que la RSE tenga como propósito contribuir al éxito general de la corporación. Para alcanzar este reto, Freeman y col. (2010) sugieren un modelo de negocios para las empresas con la creación de asociaciones con los grupos de interés y que incluya en sus procesos de RSE, la participación de los stakeholders.
Para Porter y Kramer (2002), ningún negocio puede resolver todos los problemas de la sociedad o soportar el costo de hacerlo. En su lugar, cada empresa debe seleccionar las cuestiones que se cruzan con su negocio particular. Este es un desafío para las empresas que necesitan priorizar los temas relevantes o materiales en sus planes de responsabilidad social empresarial.
Cabe destacar que realizamos un breve estudio bibliométrico, utilizando la palabra clave Fuzzy logic applied in sustainability. Los resultados indican que la aplicación de la lógica borrosa a la sostenibilidad ha sido poco investigada hasta el momento. En el Gráfico 1 se presentan los resultados de las publicaciones (sólo doce trabajos) y citas (ciento setenta y dos referencias) obtenidas a través de la Web of Science. El estudio se realizó en 23/06/2017, y las informaciones obtenidas pueden variar a lo largo del tiempo, ya que, al ser publicaciones, con el tiempo su número aumenta constantemente y se amplían los temas, a la vez que se producen conexiones interdisciplinarias.
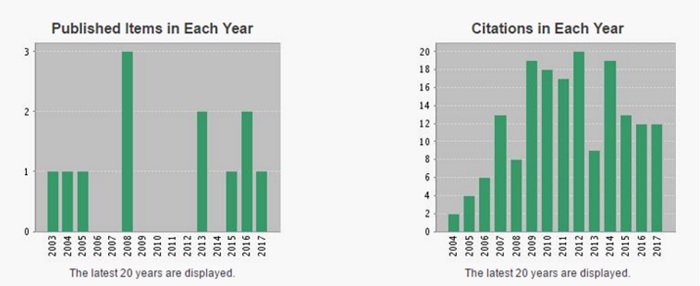
Gráfico 1. Estudio bibliométrico
Fuente: Web of Science (2017).
Resaltamos también que la búsqueda realizada puede presentar pequeñas desviaciones, ya que no todos los artículos que concuerden con las palabras Fuzzy logic applied in sustainability serán útiles en nuestra investigación. Se evidenció que existe una oportunidad de ser explorada con una investigación innovadora en esta área.
Los resultados del estudio bibliométrico indican brechas y futuras líneas de investigación con el uso de algoritmos de la lógica borrosa aplicada a la sostenibilidad, como por ejemplo, en la toma de decisiones relacionada con identificación, priorización y diálogo de stakeholders, agrupación de opiniones, definición de temas relevantes o materialidad, gestión estratégica con los grupos de interés, elección y definición de proyectos de sostenibilidad, entre otros.
En este contexto, este artículo tiene como objetivos ampliar la discusión sobre sostenibilidad en las empresas y proponer soluciones para la toma de decisiones a partir de la lógica borrosa. Para aclarar el punto, se presenta una propuesta al desarrollo sostenible de las empresas a partir de la aplicación de un algoritmo de lógica borrosa en la priorización de temas relevantes o materiales. Los resultados demuestran la utilidad de esta herramienta para las empresas en la toma de decisiones. Consideramos que nuestra contribución servirá para promover futuros estudios de investigación sobre algoritmos aplicados a la sostenibilidad de las empresas. A continuación se describe resumidamente la estructura del artículo.
En la segunda parte se exponen algunas referencias sobre la matemática de la incertidumbre y se destacan las diferencias más relevantes en relación con la matemática del azar. Más adelante, se enfatiza en las posibilidades que la teoría de los subconjuntos borrosos ofrece para abordar los problemas de decisión, en tanto ésta es considerada la principal herramienta matemática para el tratamiento de la incertidumbre. Finalmente abordaremos aquellos elementos que constituyen la base sobre la cual se asientan los conceptos fundamentales de la teoría de la decisión. En este caso, analizaremos los procesos de relación, asignación, agrupación y ordenación.
En la tercera parte se propone una aplicación de lógica borrosa para priorizar temas relevantes de los stakeholders de una empresa de deportes. En este caso se utiliza el algoritmo Expertón para alcanzar los objetivos propuestos. Los resultados confirman la validez y utilidad para las empresas en los procesos de toma de decisión. Por último, se presentan las conclusiones del artículo y las futuras líneas de investigación.
A continuación procederemos a exponer los fundamentos de la matemática de la incertidumbre.
La matemática de la incertidumbre
Se entiende por incertidumbre una forma de representar las inestabilidades y, a través de ellas, intentar comprender el papel que juegan los fenómenos en las reglas que rigen en la naturaleza. El saber científico debe describir y tratar el universo en el que realmente vivimos. Será un universo incierto, pero que responde a unas determinadas normas de conducta de los sistemas inciertos en leyes que pueden ser formalizadas de una manera cierta. Pero como muy bien afirma el Dr. Jaime Gil Aluja, “incluso de la incertidumbre se pueden extraer ciertos comportamientos expresables, la mayor parte de ellos mediante posibilidades, algunos a través de probabilidades y muy pocos por la certeza”.
La principal herramienta matemática para el tratamiento de la incertidumbre es la teoría de lo borroso y de la valuación con sus infinitas variantes, mientras que la relativa al azar es la teoría de probabilidades (Kaufmann y Gil Aluja, 1990).
La incertidumbre no posee leyes, el azar posee leyes, conocidas o no, pero que existen por hipótesis. La incertidumbre está deficientemente estructurada y cuando se la explica, se hace de manera subjetiva. El azar, por el contrario, se halla ligado al concepto de probabilidad, el cual es una medida sobre observaciones repetidas en el tiempo y/o en el espacio; el azar es una medida sobre hechos observados, constituyen una evaluación que se desearía fuera lo más objetiva posible (Ídem, pp. 1-5).
La actitud probabilística es necesariamente objetiva mientras que la modelización frente a la incertidumbre es subjetiva.
Para Kaufmann y Gil Aluja (1986), la Teoría de los Subconjuntos Borrosos es una parte de las matemáticas que se halla perfectamente adaptada al tratamiento tanto de lo subjetivo como de lo incierto. Es un intento de recoger un fenómeno tal cual se presenta en la vida real y realizar su tratamiento sin intentar deformarlo para hacerlo preciso y cierto.
El nuevo tratamiento de la incertidumbre a partir de los conceptos borrosos, ha dado lugar a una manera distinta de pensar, que reúne el rigor del razonamiento secuencial con la riqueza de la imaginación inherente a la borrosidad, que asocia las posibilidades secuenciales de la máquina a las posibilidades del cerebro humano.
La preparación de una decisión, simple o compleja, es una actividad organizativa del pensamiento en la que se combinan intuición y lógica y donde, con frecuencia, resulta difícil realizar la separación. Las matemáticas sirven a menudo de ayuda a los mecanismos de la lógica, aunque en la actualidad también somos capaces de utilizarlas para estimular la imaginación y afinar la intuición. Además estamos viviendo en la era de la información, es decir el período en que la sociedad humana ha desarrollado, en todas partes, sistemas muy potentes para el tratamiento de la información. Estos sistemas aportan, de manera directa e indirecta, nuevas y considerables posibilidades de utilizar mejor los modelos matemáticos en todo aquello que puede tener relación con el hombre y su entorno.
Los modelos tienen su soporte, la mayor parte de las veces, en teorías formales o probabilísticas. Los modelos formales toman en consideración datos ciertos, los modelos probabilísticos, datos estadísticamente mensurables o construidos a partir de razonamientos que permitan aceptar a priori leyes de probabilidad. La novedad aparece con el hecho de saber construir modelos, en el supuesto de que no puedan utilizarse ni leyes de probabilidad ni los razonamientos que con ellas se relacionan. Estos modelos son construidos, la mayor parte de las veces, utilizando propiedades definidas en la teoría de los subconjuntos borrosos y sus infinitas variantes. En lugar de partir de datos objetivos que, en muchas ocasiones, desgraciadamente no se conocen, se parte de datos subjetivos e inciertos pero aceptados generalmente como razonables. Para ello se utiliza una lógica calificada de máximo-mínimo o “maxmin”, en la que todas las hipótesis llamadas “blandas” (no mensurables) son calculadas tomando el máximo de los mínimos, lo que corresponde al comportamiento más prudente teniendo en cuenta las hipótesis existentes.
La incorporación de estos instrumentos significa una clara ruptura en relación a situaciones precedentes. Y ello, aun cuando en su desarrollo se utilicen elementos ya empleados en los estudios clásicos. La actual situación de equilibrio en la cohabitación de modelos numéricos y no numéricos en la incertidumbre, está dando paso a una mayor supremacía de estos últimos, como consecuencia de las crecientes dificultades para acotar siquiera los fenómenos sociales, económicos y de gestión. Por ello, aquellos conceptos que exigen inevitablemente ser expresados numéricamente (en la certeza o en la incertidumbre) han ido cediendo protagonismo por las dificultades de expresarlas objetiva y hasta subjetivamente, habida cuenta del contexto cada vez más incierto en el cual se inscriben (Gil Aluja, 1999).
La decisión en el ámbito empresarial resulta cada vez más compleja como consecuencia de los avances tecnológicos, la diversidad de mercados, la globalización, la multiplicidad y diversidad de productos que han motivado la necesidad de que la intuición del empresario deba ser completada por esquemas científicos cada vez más complejos. Las posibilidades que los subconjuntos borrosos ofrecen para abordar los problemas de decisión en el campo de actuación de las empresas son tan amplias, que van a enriquecer las técnicas operativas de la gestión de las empresas, principalmente en los temas actuales, como el desarrollo sostenible en las empresas.
Elementos fundamentales de la teoría de la decisión[4]
En el ámbito de las ciencias económicas y de gestión, un concepto parece primar sobre los demás, el concepto de decisión. Tanto es así que, para muchos, la economía es la ciencia de la decisión. Por esta razón, Kaufmann y Gil Aluja (1999) elaboraron la teoría de la decisión utilizando instrumentos emanados de la matemática no numérica de la incertidumbre. El resultado ha salido a luz con la publicación en Estados Unidos, de la obra Elements for a theory of decisión in uncertainty[5], construida con base en cuatro conceptos fundamentales: relación, asignación, agrupación y ordenación.
El estudio del campo decisional en las ciencias sociales pone de manifiesto que, en la práctica totalidad de los casos, la adopción de decisiones tiene lugar bien para establecer una relación, bien para afectar un “elemento” a otro “elemento”, bien para realizar agrupaciones, casi siempre homogéneas, (las cuales sirven también para separar los grupos formados) o bien para establecer un orden de prioridades, unas veces de mejor a peor (de más a menos), otras veces en sentido inverso. En cualquier caso, uno de estos elementos se hace presente en los momentos en los cuales los hombres de acción deben asumir sus responsabilidades.
En este contexto, pasamos a la descripción de aquellos elementos que constituyen la base sobre la cual se asientan los conceptos fundamentales en la decisión. En este caso, analizaremos los conceptos básicos en los procesos de relación, asignación, agrupación y ordenación. En la figura 1 presentamos los cuatro elementos que representan la pirámide de la teoría de la decisión en la incertidumbre. A partir de ellos, es posible adoptar decisiones sin necesidad de recurrir a elementos numéricos, como sucede en las viejas teorías sobre la decisión, teorías en las eran protagonistas conceptos tales como productividad, rentabilidad, economicidad, quedan ahora desplazados y sustituidos por otros. Su utilidad adquiere carta de naturaleza en unos momentos en los que la incertidumbre es tal que ni siquiera es posible acotar los fenómenos para adscribirles el más elemental de los números inciertos.
En primer lugar, partiremos nuestro estudio de investigación sobre la teoría de la decisión en la incertidumbre con la definición de la palabra relación: “Entendemos relación todo tipo de asociación capaz de poner en evidencia los niveles de conexión existente entre objetos físicos o mentales pertenecientes a un mismo conjunto o entre objetos de distintos conjuntos” (Gil Aluja, 1999, p. 33). Consideramos que esta definición pone de manifiesto la amplia posibilidad de conexiones existentes en el ámbito de la empresa, que todos los días está expuesta a diversos tipos de relaciones con sus grupos de interés. Entre ellos podemos citar a los proveedores, empleados, comunidad, administración pública, etcétera. La característica de cada uno de estos vínculos es que un sujeto cualquiera es capaz de relacionarse con todo otro sujeto, bien de manera directa o a través de otros sujetos. Además, cabe destacar que cada grupo de interés ejerce un nivel diferente de relación e influencia con la empresa. Con el paso del tiempo, el nivel o fuerza de relación también podrá variar.
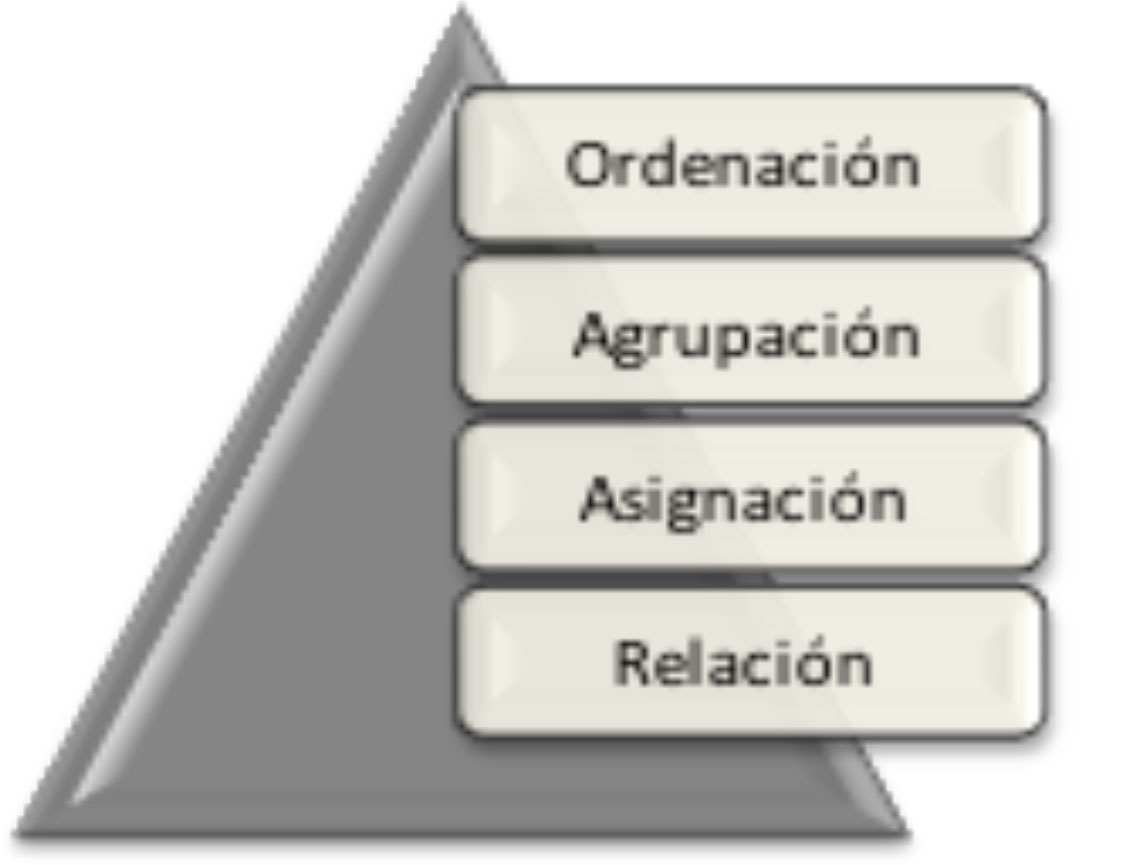
Figura 1. Elementos fundamentales de la teoría de la decisión en la incertidumbre
Fuente: elaboración propia, a partir de los datos de Gil Aluja (1999).
Hay que tener en cuenta que la relación que representa la base en el proceso de toma de decisión sobre la cual se asientan otros conceptos como asignación, agrupación y ordenación, es, en sí misma, soporte directo de la decisión. Para ello, es necesario realizar una cierta manipulación de las relaciones, utilizando convenientemente los operadores adecuados. El operador o agente conector convolución maxmin permite llegar a la conclusión de que el tiempo, el espacio, o las conexiones, según los casos, desembocan en tres situaciones a largo plazo, tipificadas por la convergencia en el límite, la periodicidad y las situaciones no estandarizables. La teoría de la decisión recurre a la pretopología, generalización de la topología, a la teoría de grafos, a la teoría reticular y a tantos otros aspectos que conforman los estudios combinatorios. Son elementos íntimamente relacionados entre sí, teniendo en cuenta que un grafo es una topología combinatoria, un retículo es un grafo y un álgebra, sea booleana o borrosa, adopta la estructura reticular (Gil Aluja, 1999). En tal sentido, el mismo autor destaca que:
En efecto, a partir de un grafo borroso, presentado en forma matricial o sagitada, permite, mediante adecuados algoritmos, conocer si existe un sólo círculo de relaciones (grafo fuertemente conexo) o varios círculos de relaciones (grafo no fuertemente conexo). En este último caso aparece la noción de clase de equivalencia o subgrafo fuertemente conexo (Ídem, p. 21).
De acuerdo con Gil Aluja (1999), al analizar la variación en las intensidades, niveles o fuerza de las relaciones, surgen particularidades que es necesario tener en cuenta en el momento de representar fielmente las realidades sociales, económicas y de gestión. Así, en multitud de supuestos tiene lugar la “degradación” en el nivel de una o varias relaciones, mientras que en otros, el transcurso del tiempo o la sucesión de etapas “fortalece” los vínculos. El tratamiento de este tipo de relaciones acumulativas presenta unas particularidades tales que no pueden ser tratadas de la misma manera que las no acumulativas. La combinatoria generada entre los diferentes elementos que forman parte directa o indirecta del contexto empresarial, afecta de forma decisiva la toma de decisiones. La toma de decisiones acostumbra a ser el resultado de un encadenamiento de ideas representativas de fenómenos que pertenecen al campo formal y/o al campo material, dirigido a la consecución de un objetivo inmediato o mediato.
Un buen ejemplo para solucionar las relaciones de incidencia o causalidad sería la aplicación de la teoría de los efectos olvidados que permite obtener “todas” las relaciones directas e indirectas, determinar algunos elementos que no son fácilmente observables y que pueden ser importantes en la toma de decisiones, sin posibilidad de error u omisión, para recuperar lo que se ha denominado “efectos olvidados”.
El segundo elemento de la teoría de la decisión en la incertidumbre que trataremos se refiere a la asignación, que es una manera muy especial de establecer relaciones. “Entendemos por asignación aquel proceso mediante el cual cada elemento de un conjunto de objetos es adscrito a otro elemento perteneciente a otro conjunto de objetos de naturaleza diferente, en base a ciertas características, exigidas a un cierto nivel.” (Gil Aluja, 1999, p. 125).
En relación con el problema de la asignación y los criterios empleados, el autor indica que:
el planteamiento del problema de la asignación parte de la existencia de tres conjuntos, normalmente finitos, de objetos físicos o mentales. El primero recoge los elementos a asignar, el segundo los elementos que deben recibir asignación y el tercero los elementos en los cuales se base el proceso asignado (cualidades, características, singularidades,…), en definitiva lo que podríamos denominar criterios de asignación. Cómo organizar el papel que juega cada uno de estos conjuntos, constituye el punto de arranque a partir del cual se desarrollan las distintas técnicas que se han ido utilizando. Consideramos que una buena manera de representar estos aspectos viene dada por la construcción de un subconjunto borroso para cada uno de los objetos a asignar tomando como referencia el conjunto de criterios de asignación (Ibídem)
Con objeto de obtener las relaciones, a partir de las cuales iniciar el proceso para la asignación, se puede recurrir a alguno de los índices capaces de expresar el “alejamiento” o acercamiento”, en su caso, entre los objetos a afectar y los objetos a los cuales debe realizarse la afectación. Entre los más conocidos, cabe citar los que surgen de la noción de distancia y los que parten de la noción de adecuación. La tarea de asignar correctamente un objeto a otro objeto, tiene, en sí misma, un carácter combinatorio, y ello entraña complejidad para alcanzar los resultados óptimos. Por esta razón, se debe poner de relieve la necesidad de hallar soluciones a través de algoritmos para el tratamiento de la asignación. Podemos destacar que el algoritmo húngaro y branch and bound, han presentado excelentes resultados en diversos campos como en los recursos humanos, finanzas, marketing, entre otros.
Por otro lado, el problema de la agrupación homogénea de objetos físicos o mentales constituye una constante para quienes deben adoptar decisiones. En efecto, son frecuentes las situaciones en las cuales el sujeto decisor se ve ante la necesidad de reunir, en bloques, “objetos” muchas veces con apariencia diferente, bien para una selección entre los componentes del mismo grupo bien para elegir un grupo entre varios de ellos (Gil Aluja, 1999).
Para lograr la construcción de un conglomerado de conocimientos a partir de la noción de afinidad, los profesores Gil Aluja y Kaufmann toman como punto de partida el concepto de relación, en su aspecto más amplio, en el sentido de que pueden existir conexiones a distintos niveles entre elementos de dos conjuntos referenciales finitos. La presentación de estas relaciones mediante una relación borrosa, normalmente rectangular, permite un amplio juego del que se derivan interesantes reflexiones. Una de ellas hace referencia a la flexibilidad derivada de la posibilidad de obtener, a partir del tratamiento mediante α-cortes, un abanico de matrices booleanas capaz de permitir la adaptabilidad necesaria en la formulación de agrupaciones, considerando los niveles deseados de homogeneidad.
Kaufmann y Gil Aluja definen las afinidades como “aquellas agrupaciones homogéneas a determinados niveles, estructuradas ordenadamente, que ligan elementos de dos conjuntos de distinta naturaleza, relacionados por la propia esencia de los fenómenos que representan” (Gil Aluja, 1999, p. 186).
Se puede observar la existencia de tres aspectos configuradores del concepto de afinidad. El primero hace referencia al hecho de que la homogeneidad de cada agrupación se halla ligada al nivel escogido. Según la exigencia de cada característica (elementos de uno de los conjuntos) se asignará un nivel más o menos elevado definidor del umbral a partir del cual existe homogeneidad. El segundo expresa la necesidad de que los elementos de cada uno de los conjuntos se hallen ligados entre sí por ciertas reglas de la naturaleza en unos casos o por la voluntad humana de otros. El tercero exige la construcción de una estructura constitutiva de un cierto orden susceptible de permitir la posterior decisión (Ídem).
Es importante destacar la importancia de los cierres de Moore en la obtención de afinidades, la representación de estas agrupaciones mediante estructuras reticulares que ponen en evidencia las afinidades, las subrelaciones máximas de similitud y las agrupaciones a partir del concepto de clan. Este conjunto de elementos va a facilitar a toma de decisión en la incertidumbre.
Se llega, finalmente, a la noción de orden. Constituye el concepto que culmina la pirámide de la teoría de la decisión en la incertidumbre. El desafío está en elaborar una estructura teórica capaz de suministrar elementos suficientes para la adopción de decisiones basadas en la ordenación, cuando la incertidumbre no permite la estimación de magnitudes numéricas, ni en el ámbito de la certeza o del azar, ni en el campo de la incertidumbre (Gil Aluja, 2001).
Efectivamente, cuando somos capaces de ordenar de alguna manera un conjunto de elementos (objetos) y este orden se halla establecido según otro conjunto de elementos (normalmente de naturaleza distinta), es posible la construcción de una escala con apreciaciones crecientes (o decrecientes). Se obtienen, así, óptimos y subóptimos sin la necesidad de recurrir a conceptos cardinales. Para Gil Aluja (1999) “el orden es una graduación en las preferencias de objetos físicos o mentales, establecida en base a la apreciación objetiva o subjetiva de sus propiedades, características o singularidades.” (p. 265).
Con objeto de obtener estructuras capaces de conducirnos hacia algoritmos aptos para la ordenación, resulta muy importante también, la presentación de las relaciones a través de grafos en las formas matriciales y sagitadas. A partir de ellas, se recurre a ciertos desarrollos que permiten una suficiente gama de caminos capaces de cubrir un amplio abanico de problemas hasta hace poco sin solución satisfactoria. Una vez formadas las clases de equivalencia, nos hallamos en disposición de establecer un orden entre las mismas. Para ello, existen varios caminos cuya utilización depende, entre otros factores, de los planteamientos realizados y de los fines a alcanzar. Podemos destacar dos métodos, el que parte de la noción de función ordinal de un grafo y el que utiliza las propiedades de la Composición P-latina. En un sistema social y económico marcado por la incertidumbre el concepto de orden ocupa un puesto de privilegio para la decisión. Cuando no es posible obtener un cuadro “valorado” de objetos, apelar a un “orden no cuantificado” de estos, puede resultar suficiente para una decisión adecuada.
Método de los expertones
En este apartado se describe la metodología y enseguida su aplicación en una empresa de deportes.
El “método de los expertones” que representa una importante extensión de los subconjuntos borrosos cuya idea y desarrollo se debe a A. Kaufmann. Para autores como Gil Lafuente y col. (2007),
el avance que representan los expertones en relación con otros instrumentos de tratamiento de la incertidumbre viene dado por el hecho de que permite a la vez una buena agregación de la opinión de varios expertos y que éstos expresan sus opiniones con la libertad que proporcionan los números borrosos.
Veamos, muy brevemente, cómo se construye un expertón a partir de sus propiedades. Se conoce que todo expertón posee la propiedad de la monotonía creciente horizontal no estricta, es decir, la función característica de pertenencia de la función de pendiente positiva es menor o igual a la función característica de pertenencia de la función de pendiente negativa. Y por otro lado todo expertón posee monotonía creciente vertical no estricta, salvo en el nivel 0 que siempre toma el valor 1. Por tanto, diremos que:
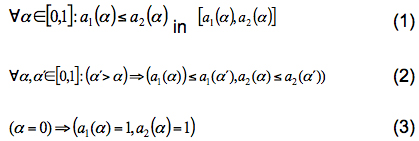
Consideramos que la valuación de cada experto expresa un nivel de verdad mediante la escala endecadaria (11 valores entre 0 y 1, ambos incluidos) que puede ser explicada genéricamente de la siguiente forma:
0: falso
0.1: prácticamente falso
0.2: casi falso
0.3: bastante falso
0.4: más falso que verdadero
0.5: ni verdadero, ni falso
0.6: más verdadero que falso
0.7: bastante verdadero
0.8: casi verdadero
0.9: prácticamente verdadero
1: verdadero
A partir de aquí se va a iniciar un proceso de agregación dirigido a la transformación de opiniones en una valuación representativa. En primer lugar será preciso obtener una estadística de las opiniones para conocer la cantidad de veces que los expertos han expresado la misma opinión. A partir de las frecuencias acumuladas obtenidas, se procede al cálculo de las frecuencias acumuladas relativas, dividiendo los valores anteriores por el número total de opiniones. El resultado obtenido es el denominado "expertón". Su significación no sólo reside en la obtención de las frecuencias relativas asignadas a la función característica de pertenencia, sino que la información suministrada permite conocer la distribución y la tendencia de unas opiniones subjetivas cuyo número puede ser muy variable.
El expertón es en sí una opinión agregada representativa de todas las que han sido consideradas en la muestra. Con objeto de dar una representación simplificada de un expertón, se puede recurrir a la obtención de la esperanza matemática. Todos los operadores que pueden ser utilizados con variables o intervalos de confianza en [0,1] también pueden utilizarse con expertones, y estas operaciones son válidas para un número cualquiera de expertones.
Esta metodología puede facilitar la toma de decisiones mediante la obtención de datos cualitativos a partir del diálogo con los diferentes grupos de interés. Ello constituye una innovación y una herramienta útil a ser utilizada en los procesos de agregación y unificación de opiniones contradictorias o expectativas divergentes entre sus grupos de interés. Además, el modelo permite conocer la distribución por niveles en la función característica de pertenencia de los valores agregados.
Algoritmo aplicado en una empresa de deportes
Este apartado se presenta una aplicación del método de los expertones para priorizar temas relevantes de los stakeholders de una empresa multinacional deportes. El nombre la empresa no será revelado por razones de confidencialidad. Esta empresa se dedica a la fabricación de calzado, ropa deportiva y otros productos relacionados con el deporte y la moda. La empresa emplea a más de 60.000 personas en más de 160 países y produce más de 850 millones de unidades de producto cada año.
Nuestro estudio se centra en conocer las expectativas de las partes interesadas en cuanto al cumplimiento de los contenidos del informe de sostenibilidad preparado por una empresa de acuerdo con el Global Reporting Initiative (GRI). Para lograr este objetivo se intentará analizar la evaluación de materialidad de la empresa.
El GRI define la materialidad como "Temas e indicadores que reflejan los impactos económicos, ambientales y sociales significativos de la organización, o que influirían sustancialmente en las evaluaciones y decisiones de las partes interesadas". "La materialidad es el umbral en el cual un tema o indicador llega a ser lo suficientemente importante como para ser reportado". Los datos del estudio fueron tratados con estricta confidencialidad. Por lo tanto, como lo sugiere el GRI, la empresa para desarrollar su "Informe de Sostenibilidad" debe estar involucrada en una extensa red de expertos de diversos grupos de interés, entre los que se incluyen, en este caso:
- 1.
1. Analista
2. Inversor
3. Organización No Gubernamental (ONG)
4. Académico
5. Consultor
6. Medios de comunicación
7. Otro
El objetivo es la evaluación y priorización de los temas económicos, y que a partir de los resultados, la empresa puede o no establecer compromisos específicos. Una vez presentado a los siete expertos sobre la importancia de las cuestiones de sostenibilidad a través de la encuesta en línea, se pide que indique su punto de vista con la escala [0,1], por lo que, con la estimación más cercana a 1, mejor y más de acuerdo con las expectativas de los stakeholders en relación a los siguientes temas:
- 1.
1. Prácticas comerciales éticas
2. Gobierno, gestión de riesgos, cumplimiento legal
3. Compras locales
4. Rendimiento financiero
5. Impacto económico
El enfoque que sigue se basa en la consideración de elementos y datos que surgen de una demanda real. Los resultados pueden permitir una profunda reflexión y aplicación a los campos académicos y profesionales, de acuerdo con los datos recogidos tendrían las opiniones de los siete expertos, como se muestra en la tabla 1.
| Experto | Valuación | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0.8 | 0.8 | 0.8 | 0.8 | 0.6 |
| 2 | 0.8 | 0.7 | 0.7 | 0.8 | 0.7 |
| 3 | 0.7 | 0.7 | 0.7 | 0.6 | 0.6 |
| 4 | 0.7 | 0.7 | 0.6 | 0.5 | 0.6 |
| 5 | 0.7 | 0.8 | 0.6 | 0.7 | 0.7 |
| 6 | 0.6 | 0.6 | 0.8 | 0.6 | 0.4 |
| 7 | 0.8 | 0.8 | 0.7 | 0.6 | 0.6 |
La primera tarea será obtener las frecuencias acumuladas (F.A.) de las opiniones, para conocer el número de veces que los expertos han expresado la misma valoración, como se muestra en la tabla 2.
| 1 | 2 | 3 | 4 | 5 | ||||||
| F. A. | Nº veces | F. A | Nº veces | F. A | Nº veces | F. A | Nº veces | F. A | Nº veces | |
| 0 | 7 | 0 | 7 | 0 | 7 | 0 | 7 | 0 | 7 | 0 |
| 0.1 | 7 | 0 | 7 | 0 | 7 | 0 | 7 | 0 | 7 | 0 |
| 0.2 | 7 | 0 | 7 | 0 | 7 | 0 | 7 | 0 | 7 | 0 |
| 0.3 | 7 | 0 | 7 | 0 | 7 | 0 | 7 | 0 | 7 | 0 |
| 0.4 | 7 | 0 | 7 | 0 | 7 | 0 | 7 | 0 | 7 | 1 |
| 0.5 | 7 | 0 | 7 | 0 | 7 | 0 | 7 | 1 | 6 | 0 |
| 0.6 | 7 | 1 | 7 | 1 | 7 | 2 | 6 | 3 | 6 | 4 |
| 0.7 | 6 | 3 | 6 | 3 | 5 | 3 | 3 | 1 | 2 | 2 |
| 0.8 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 0 | 0 |
| 0.9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
A partir de la frecuencia acumulada obtenida se realiza el cálculo de las frecuencias relativas (Tabla 3) dividiendo los valores anteriores por el número total de vistas, en nuestro caso son siete.
| Frecuencias relativas | |||||
| 1 | 2 | 3 | 4 | 5 | |
| 0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 0.1 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 0.2 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 0.3 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 0.4 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 0.5 | 1.0 | 1.0 | 1.0 | 1.0 | 0.9 |
| 0.6 | 1.0 | 1.0 | 1.0 | 0.9 | 0.9 |
| 0.7 | 0.9 | 0.9 | 0.7 | 0.4 | 0.3 |
| 0.8 | 0.4 | 0.4 | 0.3 | 0.3 | 0.0 |
| 0.9 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
El resultado se denomina “Experton”. El Experton es en sí mismo una vista agregada representativa de todo lo que se ha considerado en la muestra, para dar una representación simplificada de un Experton, se puede recurrir a la obtención de la esperanza matemática, conforme descrito en la tabla 4.
El resultado muestra un orden de prioridades en relación a los temas relevantes o materiales de los stakeholders a través de la agregación de sus puntos de vista. En este caso, sigue el orden de prioridades: La presentación de los resultados también puede ser plasmado en una matriz de materialidad (Figura 2) que toma en cuenta los criterios de impacto y relevancia para la empresa.
- 1.
1. Prácticas comerciales éticas
2. Gobierno, gestión de riesgos, cumplimiento legal
3. Compras locales
4. Rendimiento financiero
5. Impacto económico
| Esperanza matemática | |
| ε1 = | 0.73 |
| ε2 = | 0.73 |
| ε3 = | 0.70 |
| ε4 = | 0.66 |
| ε5 = | 0.60 |
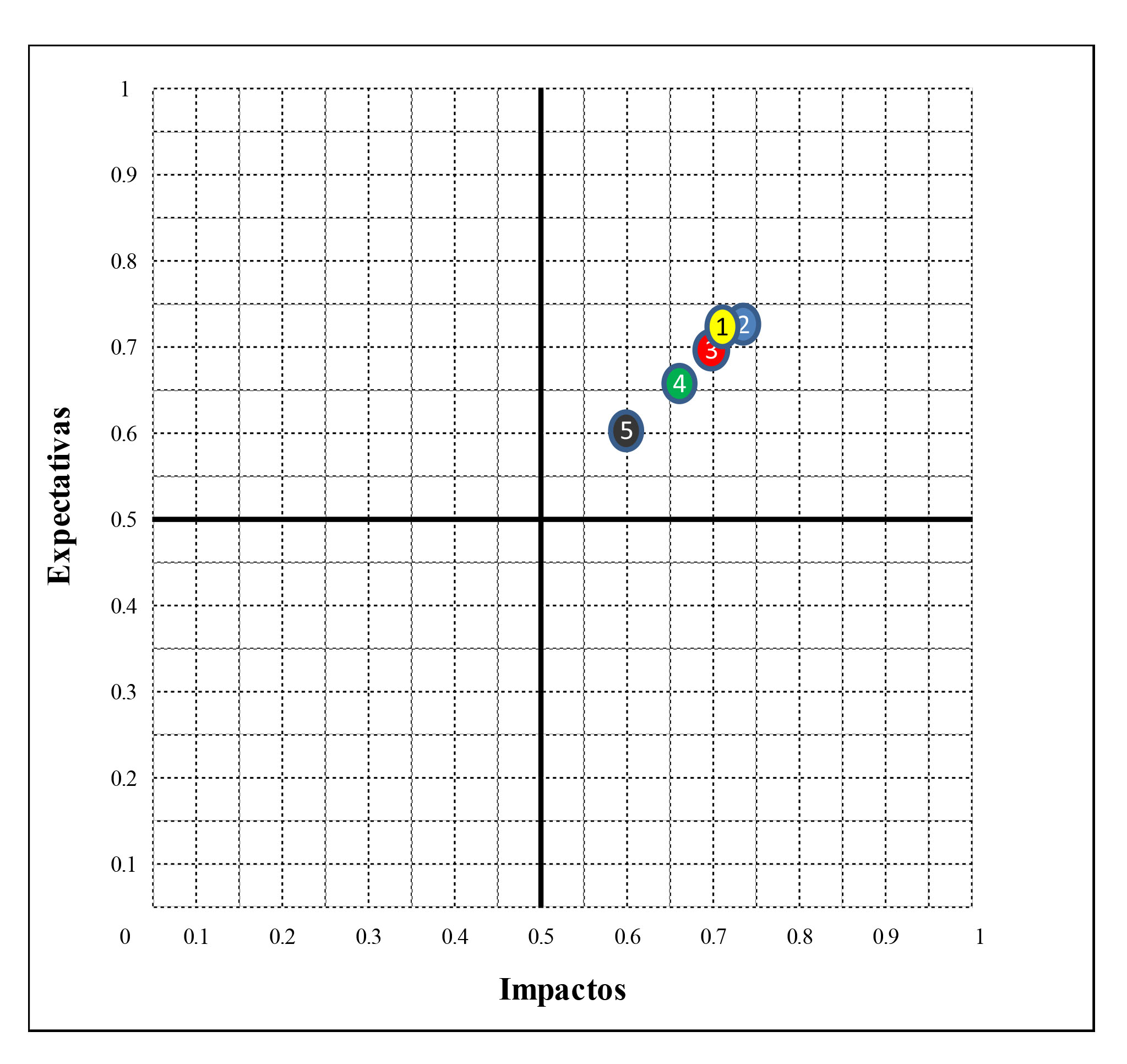
Figura 2. Matriz de materialidad
Fuente: elaboración propia (2017).
El modelo propuesto puede ampliarse de acuerdo con los requisitos de las preguntas, el número de expertos y sectores empresariales participantes. A continuación se presentan las conclusiones del estudio y futuras líneas de investigación.
Conclusiones
La investigación sobre la sostenibilidad en las empresas indica que la necesidad de encontrar herramientas de toma de decisión para apoyar a los empresarios, principalmente en la gestión y el diálogo con los stakeholders. Por esta razón, ofrecemos una herramienta de lógica borrosa, basada en el uso del Método de los Expertones.
Esta metodología puede facilitar la toma de decisiones mediante la obtención de datos cualitativos a partir de un diálogo con diversas partes interesadas. Se trata de una innovación y una herramienta útil en los procesos de agregación y unificación de opiniones o expectativas diferentes entre las partes. Además, el modelo permite conocer la distribución por niveles en la función característica de pertenencia de los valores agregados
El resultado permitió conocer y priorizar las expectativas de los stakeholders sobre temas relevantes relacionados con la dimensión económica, basada en el cumplimiento de los contenidos del informe de sostenibilidad de Global Reporting Iniciative (GRI).
Cabe destacar que los resultados fueron ilustrados gráficamente en una matriz de materialidad, para facilitar la gestión de los temas priorizados. Con los resultados, la empresa de deportes debe revisar sus compromisos y cuestiones relacionadas con la materialidad del enfoque económico, tales como: (1) Prácticas comerciales éticas, (2) Gobierno, gestión de riesgos, cumplimiento legal, (3) Compras locales, (4) Rendimiento financiero y (5) Impacto económico.
La principal contribución de este trabajo es proporcionar un modelo que ayude a los empresarios en la agregación de opiniones relacionadas con las partes interesadas. Además, como indica el GRI, este proceso sirve como documentación y explicación de cómo se han evaluado y priorizados tales factores al elaborar el informe de sostenibilidad.
Consideramos que nuestra contribución servirá para apoyar la investigación futura en el campo de la sostenibilidad empresarial, contribuirá al desarrollo sostenible y en la aplicación de la metodología de evaluación de la materialidad.
Agradecimientos
Le agradecemos a CENTRUM Católica por el soporte en esta investigación.
Referencias
Bowen, H.R. (1953). Social responsibilities of the businessman. Nueva York: Harper.
Carroll, A.B. (1979). A three dimensional conceptual model of corporate performance. Academy of Management Review, 4(4): 497-505.
Elkington, J. (1994). Towards the Sustainable Corporation: Win-Win-Win Business Strategies for Sustainable Development. California Management Review, 36(2): 90-100.
Elkington, J. (1999), Triple bottom line revolution: reporting for the third millennium. Australian CPA, 69(11): 75-76.
Freeman, R.E. (1984). Strategic Management: A Stakeholder Approach. Pitman Series in Business and Public Policy. Nueva York: Cambridge University Press.
Freeman, R.E., Harrison, J.S., Wicks, A.C., Parmar, B. y Colle, S. (2010). Stakeholder theory, the state of the art. Nueva York: Cambridge University Press.
Gil Aluja, J. (2001). Entre la epistemología y la lógica. Decisión y algoritmo de ordenación. Cuadernos de Gestión, 1(1): 151-159.
Gil Aluja, J. (1999). Elementos para una teoría de la decisión en la incertidumbre. Santiago de Compostela: Editorial Miladoiro.
Gil Aluja, J. (1999). Elements for a theory of decision in uncertainty. Boston: Kluwer Academic Publishers.
Gil Lafuente, A.M. y Gil Lafuente, J. (2007). Modelos y Algoritmos para el tratamiento de la creatividad en la gestión empresarial. Santiago de Compostela: Editorial Milladoiro.
Hart, S.L. y Milstein, M. (2003). Creating Sustainable Value. Academy of Management Executive, 17(2): 56-69.
Kaufmann, A. y Gil Aluja, J. (1990). Las matemáticas del azar y de la incertidumbre. Elementos básicos para su aplicación en economía. Madrid: Editorial Centro de Estudios Ramón Areces.
Kaufmann, A. y Gil Aluja, J. (1986). Introducción de la teoría de los subconjuntos borrosos a la gestión de las empresas. Santiago de Compostela: Editorial Milladoiro.
Lee, M.D.P. (2008). A review of the theories of corporate social responsibility: Its evolutionary path and the road ahead. International Journal of Management Reviews, 10(1): 53–73.
Paula, L.B. (2011). Modelos de gestión aplicados a la sostenibilidad empresarial. Tesis Doctoral. Universidad de Barcelona, España. [En línea. Consultado en 26 de julio del 2017]. Disponible en http://hdl.handle.net/10803/32219.
Porter, M., y Kramer, M. (2011). Creating Shared Value. Harvard Business Review, 89. Disponible en: https://hbr.org/2011/01/the-big-idea-creating-shared-value.
Porter, M. y Kramer, M.K. (2002). The competitive advantage and corporate philanthropy. Harvard Business Review, 80 (12): 55-69.
Steven L. Wartick y Cochran, P.L. (1985). The Evolution of the Corporate Social Performance Model. The Academy of Management Review, 10(4): 758-769.
Notas