Artículo original
Estudio teórico de la descomposición térmica del ácido malónico en fase gaseosa y en disolución acuosa
Theoretical study of the thermal decomposition of malonic acid in gas phase and aqueous solution
Estudio teórico de la descomposición térmica del ácido malónico en fase gaseosa y en disolución acuosa
Revista Cubana de Química, vol. 31, núm. 2, p. 0, 2019
Universidad de Oriente
Recepción: 05 Junio 2018
Aprobación: 11 Febrero 2019
RESUMEN: En este trabajo se presenta el estudio computacional de la reacción de descomposición térmica del ácido malónico. Se modeló mediante dos mecanismos, a cinco temperaturas, en fase gaseosa y en disolución acuosa. Los cálculos fueron realizados mediante la teoría de los funcionales de la densidad. Para las condiciones estudiadas de la reacción, la constante de velocidad fue calculada con la ecuación de Eyring-Polanyi. Los resultados fueron comparados con los valores experimentales reportados. Otro tipo de cálculo realizado fueron los orbitales naturales de enlace. Los resultados obtenidos permitieron discutir diferentes aspectos acerca de los mecanismos de reacción planteados.
Palabras clave: B3LYP, M05-2X, ácido malónico, descomposición térmica, mecanismo de reacción.
ABSTRACT: In this work, the computational study of the thermal decomposition of malonic acid is presented. It was followed by two mechanisms, at five temperatures, in gas phase and in aqueous solution. The calculations were carried out by means of the density functional theory. The rate constant of the reaction for the studied conditions was calculated with the Eyring-Polanyi equation. The results were compared with the reported experimental values. Another type of calculation performed were the natural bond orbitals. The results obtained allowed to discuss different aspects about the proposed reaction mechanisms.
Keywords: B3LYP, M05-2X, malonic acid, thermal decomposition, reaction mechanism.
Introducción
El ácido malónico o propanodioico, CH2(COOH)2, es un ácido dicarboxílico de gran interés industrial, utilizado como un intermedio o como una sustancia de partida para la síntesis de otros productos.1-3 El ácido malónico ha sido reportado como una molécula presente en varias rutas metabólicas de sistemas biológicos.4-7
Sus múltiples aplicaciones han suscitado un interés creciente por el estudio de sus propiedades y su reactividad química. Este ácido descompone térmicamente a temperaturas moderadamente altas. Se han realizado estudios de su descomposición en fase sólida 8,9, como liquido sub-enfriado 8, en fase gaseosa 10, en disolución acuosa 3,11,12 y en otros solventes no acuosos.8,13,14 Con temperaturas de trabajo que abarcan valores desde 80 hasta 200 °C. La descomposición ocurre unimolecularmente para producir dióxido de carbono y ácido acético en iguales proporciones.10 Los mismos productos han sido reportados para la descomposición del ácido malónico cuando se ha llevado a cabo en atmósferas de CO2 o de N2.15 Los estudios cinéticos realizados previamente reportan una cinética de primer orden.3,10-14,16
Estudios de efecto isotópico sobre la reacción de descomposición del ácido malónico han sugerido que la reacción ocurre en forma concertada mediante un estado de transición de seis miembros y que ambos grupos carboxílicos están involucrados en el estado de transición.17 Otra investigación de la termólisis del ácido malónico en fase gaseosa indica que la reacción ocurre mediante un mecanismo concertado, que implica la transferencia intramolecular de un átomo de hidrógeno, a través de un estado de transición cíclico de cuatro centros.10 Cruz-Castañeda y colaboradores realizaron la termólisis del ácido malónico a 95 °C y plantearon un mecanismo en dos etapas para la formación de ácido acético y dióxido de carbono, como productos finales de la descomposición.12 En estudios cinéticos llevados a cabo en solventes no acuosos, se ha encontrado que la energía de activación de la reacción disminuye según aumenta la disponibilidad de electrones desapareados en el átomo nucleofilico 13 y que la constante de velocidad de la reacción llevada a cabo en disolución varía dependiendo de la naturaleza del solvente utilizado.14 La reacción también ha sido estudiada teóricamente 18 a MP2(Full)/6-31G*, para los canales de reacción que implican estados de transición de 6 y de 4 centros, realizadas en fase gaseosa y en disolución. Los investigadores encontraron que la vía a través de un estado de transición cíclico de 6 centros está favorecida energéticamente.
Otros tipos de estudios realizados sobre el ácido malónico han sido la reacción de disociación en disolución acuosa, para la cual se ha reportado una baja velocidad comparada con la velocidad de descarboxilación 11 y también se ha reportado el cálculo de las entalpías estándar de formación del ácido malónico y los productos de su disociación en disolución acuosa.19
En este trabajo presentamos el estudio computacional de la reacción del ácido malónico en fase gaseosa y en disolución acuosa. La reacción se modeló mediante dos mecanismos de reacción diferentes. El primero consiste en la formación de ácido acético y dióxido de carbono en un solo paso, a través de un estado de transición cíclico de cuatro miembros, así como fue propuesto por Cao y Back.10 El estudio del segundo mecanismo se basó en el propuesto por Cruz-Castañeda y colaboradores 12, el cual ocurre en dos etapas. La primera, mediante un estado de transición cíclico de seis centros, donde hay una transferencia intramolecular de H y una descarboxilación, lo que permite la formación de una molécula de 1,1-etenodiol y una molécula de dióxido de carbono. Por razones que se discutirán más adelante, en este trabajo se descartó la segunda etapa del mecanismo mencionado y el estudio se centró en la primera etapa de la reacción.
Materiales y métodos
Todas las moléculas involucradas en los mecanismos de reacción estudiados fueron optimizadas en el paquete computacional Gaussian 09.20 Mediante la teoría de los funcionales de la densidad (DFT, por sus siglas en inglés). Con los funcionales B3LYP 21,22,23 y M05-2X 24 y conjuntos de base 6-31G(d,p) y 6-31+G(d,p)25, respectivamente. Se realizaron cálculos de frecuencia vibracional para obtener los parámetros cinéticos y termodinámicos de las reacciones, ello también permitió caracterizar cada estructura como un mínimo o un punto silla dentro de la superficie de energía potencial. Las energías vibracionales del punto cero fueron corregidas mediante factores de escalamiento de 0,985 7 y 0,963 1 26 para los métodos B3LYP/6-31G(d,p) y M05-2X/6-31+G(d,p), respectivamente. Los cálculos fueron realizados a cinco temperaturas diferentes dentro del rango de 365,2 -424,2 K y a una presión de 1 atm. Los valores de entalpías y entropías fueron evaluados de acuerdo a las ecuaciones de la termodinámica estándar.27) Los cálculos en disolución acuosa fueron realizados mediante el modelo continuo polarizable, se usó el formalismo de la ecuación integral (IEFPCM).28 La constante de velocidad, k(T), se calculó mediante la teoría clásica del estado de transición (TST) de acuerdo a la ecuación de Eyring-Polanyi.29,30 Cálculos de la coordenada intrínseca de la reacción (IRC) 31 fueron realizados sobre cada uno de los estados de transición, para verificar que ellos conectan con los respectivos puntos mínimos estacionarios correspondientes a los reactivos y productos de las reacciones estudiadas.
La técnica de partición poblacional, Natural bond orbital (NBO) 32-34, implementada en el paquete computacional Gaussian 09.20 Se utilizó para obtener las cargas naturales totales atómicas y los índices de enlace de Wiberg 35 utilizados para hacer un seguimiento a la reacción.
Resultados y discusión
Mecanismo y geometría molecular
La reacción de descomposición térmica del ácido malónico fue estudiada a dos diferentes niveles de teoría, B3LYP/6-31G(d,p) y M05-2X/6-31+G(d,p). La reacción fue modelada mediante dos mecanismos de reacción, como se muestra en la fig. 1.
El primer mecanismo (1a) consiste en un proceso de una etapa que ocurre por la migración 1,3 de hidrógeno. A través de un estado de transición cíclico de cuatro centros, el cual permite la formación de ácido acético y dióxido de carbono.
El segundo mecanismo (1b) corresponde a un proceso de dos etapas, en la primera ocurre una descarboxilación que conlleva a la formación de una molécula de 1,1-etenediol y una molécula de dióxido de carbono. El estado de transición para la primera etapa presenta una geometría cíclica de seis centros. En la segunda etapa se da la transferencia intramolecular de H en un proceso del tipo ceto-enol para generar el ácido acético.
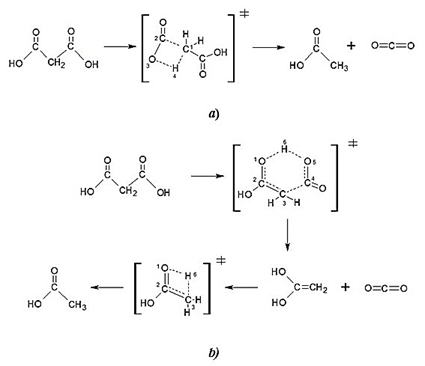
Fig. 1
Mecanismos de reacción estudiados para la descomposición térmica del ácido malónico. a) mecanismo en una etapa. b) mecanismo en dos etapas
Cada estructura molecular de las sustancias involucradas en las reacciones estudiadas fue completamente optimizada a los niveles de teoría M05-2X/6-31+G(d,p) y B3LYP/6-31G(d,p). En la figura 2 se muestran las estructuras optimizadas. TS4a representa el estado de transición para el mecanismo representado en la fig. 1a, TS6b y TS4b, se refieren a los estados de transición de 6 y 4 centros respectivamente, según el mecanismo representado en la fig. 1b.
Los estados de transición para los dos mecanismos estudiados se caracterizan por tener una frecuencia imaginaria, cuyos valores a M05-2X/6-31+G(d,p) son: TS4a (ν = 1977i cm-1), TS6b (ν = 451i cm-1), y TS4b (ν = 2068i cm-1)
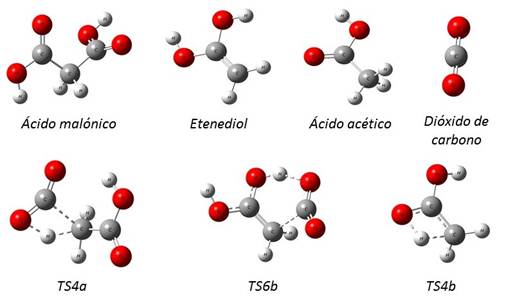
Fig. 2
Geometrías optimizadas a M05-2X/6-31+G(d,p) para todas las especies involucradas en las reacciones estudiadas
Cinética de la reacción
Termodinámicamente el ácido acético tiene mayor estabilidad que la molécula del 1,1-etenediol. 36-43 Por ejemplo, los cálculos realizados para la reacción a 365,2 K y a M05-2X/6-31+G(d,p) en fase gaseosa y en disolución acuosa indican que el ácido acético es más estable que el 1,1-etenediol por 118.1 y 105.6 kJ.mol-1 respectivamente. Los resultados cinéticos en disolución acuosa a B3LYP/6-31G(d,p), muestran que la formación de ácido acético desde el 1,1-etenediol tiene un valor para la barrera energética de 183,3 kJ.mol-1 (ver tabla 1). La magnitud de ΔG≠ es tan alta que la constante de velocidad para esa reacción es del orden de 10-14 s-1 a 365,2 K, lo que permitiría un tiempo de vida media para el 1,1-etenediol del orden de 1013 s y por tanto debería ser detectado en los análisis experimentales. Los resultados obtenidos del mecanismo de reacción propuesto para la segunda etapa de la fig. 1b, van en contradicción con lo observado experimentalmente, ello nos permite concluir que la reacción para la cual ocurre el proceso de equilibrio ceto-enol debe proceder por un mecanismo de reacción diferente al planteado.
Nguyen all. 41 estudiaron el mecanismo de reacción para la hidratación de una molécula de ceteno hasta ácido acético, en los mecanismos que estudiaron se produce 1,1-etenediol como intermedio de la reacción para luego tautomerizar hasta ácido acético. Para la reacción de isomerización, los investigadores plantearon un mecanismo asistido por una molécula de agua (presente como vapor de agua cuando la reacción se lleva a cabo en fase gaseosa) la cual presenta un efecto catalítico y permite que la reacción transcurra de manera rápida. Otro importante aspecto a tener en cuenta, y que además hace que la conversión del 1,1-etenediol hasta ácido acético sea una etapa rápida y por tanto no contribuya al valor de la constante de velocidad observada experimentalmente, tiene que ver con el efecto de superficie existente, que actúa catalíticamente en el proceso de reacción.41
Por lo anterior, de aquí en adelante la discusión acerca de los mecanismos de reacción propuestos (como fueron representados en la fig. 1) se limitará al mecanismo 1a y a la primera etapa en el mecanismo 1b (descartando que la segunda etapa del mecanismo 1b sea la etapa limitante de la velocidad).
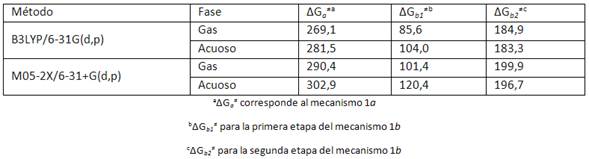
La tabla 1 resume los valores calculados para las barreras energéticas de las reacciones en los mecanismos propuestos. Éstos fueron obtenidos mediante los cálculos a B3LYP/6-31G(d,p) y M05-2X/6-31+G(d,p).
La reacción mediante el mecanismo 1a (a través de TS4a) tiene una barrera energética más alta para la reacción en fase gaseosa y en disolución acuosa que cuando la reacción procede a través del mecanismo 1b. La diferencia en las barreras energéticas son cercanas a 180 kJ.mol-1, ello corrobora la mayor estabilidad para el estado de transición cíclico de 6 miembros respecto a un estado de transición de 4 miembros. Los resultados están de acuerdo con las conclusiones obtenidas del estudio realizado.18
Los resultados de la reacción en disolución acuosa indican que ésta ocurre de manera más lenta cuando se lleva a cabo en fase gaseosa. Se evidencia por un incremento en la magnitud de la energía libre de activación (ΔG≠). La diferencia entre los ΔG≠ de la reacción en la fase gaseosa y la fase acuosa es de 12.4 kJ/mol a B3LYP/6-31G(d,p) y de 12,5 kJ/mol a M05-2X/6-31+G(d,p). Ello es indicativo de la presencia de un estado de transición poco polar, lo cual está de acuerdo con Huang y colaboradores 18 que concluyeron que la polaridad del solvente no genera un importante efecto sobre la barrera energética de la reacción. En consecuencia el solvente no presenta un efecto estabilizador o si lo hace ocurre en proporción mínima en comparación a la mayor interacción que debe tener con el ácido malónico (reactivo), por ejemplo, por la formación de puentes de hidrogeno intermoleculares.
En la tabla 2 se presentan las ecuaciones de Arrhenius experimentales para la reacción de descomposición térmica del ácido malónico. Los estudios de la descomposición se han llevado a cabo en diferentes estados: como sólido fundido, en solución acuosa y en fase gaseosa.
El perfil de la reacción de descomposición térmica del ácido malónico calculado con el método M05-2X/6-31+G(d,p) se presenta en la fig. 3. Se nota que la reacción se favorece cinética y termodinámicamente cuando es llevada a cabo en fase gaseosa en referencia a la misma reacción en disolución acuosa.
| Rango de T (K) | Ecuación de Arrhenius linealizadaa | Eab (kJ/mol) | Ab (s-1) | Fase | Ref. |
| 399,0 - 426,8 | ln k = 34,8 - 16 356 T-1 | 136,0 | 1,3×1015 | sólido fundido | [8] |
| 353,2 - 363,2 | ln k = 30,9 - 15 519 T-1 | 129,0 | 2,6×1013 | disolución acuosa | [11] |
| 365,2 - 424,2 | ln k = 30,3 - 15 486 T-1 | 128,8 | 1,5×1013 | gas | [10] |
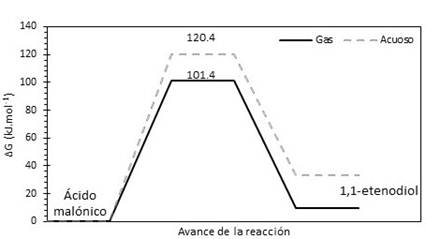
Fig. 3
Perfil de reacción para la descomposición del ácido malónico (mecanismo 1b). Calculado a M05-2X/6-31+G(d,p) a 365,2 K, en fase gaseosa y en disolución acuosa
La tabla 3 muestra las constantes de velocidad (k) para los canales de reacción estudiados, fueron calculadas mediante la teoría del estado de transición convencional, se asumió una cinética de primer orden y un coeficiente de transmisión de 1. Los cálculos fueron realizados en fase gaseosa y en disolución acuosa con los métodos B3LYP/6-31G(d,p) y M05-2X/6-31+G(d,p) en el rango de temperatura de 365,2 - 424,2 K.
Las constantes de velocidad calculadas con el método M05-2X/6-31+G(d,p) se acercan más a las constantes experimentales reportadas. Los valores obtenidos con el método B3LYP/6-31G(d,p) se hallan más alejados de los valores experimentales.
Se encontró que la relación kComp/kExp es de aproximadamente cinco cuando los cálculos computacionales se realizan a M05-2X/6-31+G(d,p) para la fase acuosa. Donde kComp es la constante obtenida computacionalmente y kExp es la constante experimental obtenida a la misma temperatura. Esa misma relación para las constantes en fase gaseosa presenta un valor mucho más alto.
Las ecuaciones de Arrhenius computacionales fueron determinadas a partir de las gráficas de ln k y T-1 como se muestran en las figuras 4 y 5. La energía de activación (Ea) y el factor pre-exponencial (A) también han sido tabulados en la tabla 3.
Los parámetros cinéticos experimentales (k, Ea y A) para la reacción en fase gaseosa presentan muy poca diferencia respecto a los valores obtenidos para la reacción en disolución acuosa. Por ejemplo la diferencia en las energías de activación de la reacción en fase gaseosa respecto al mismo en la fase acuosa (ΔEa(a-g)) es de solo 0,2 kJ.mol-1. A partir de los resultados a M05-2X/6-31+G(d,p), esa diferencia es de 24 kJ.mol-1. El factor pre-exponencial calculado está en buen acuerdo con el valor experimental para la reacción en las dos fases estudiadas y se encuentra dentro del rango de valores característicos para reacciones de primer orden.
| Método | B3LYP/6-31G(d,p) | M05-2X/6-31+G(d,p) | Experimentala | |||
| Gas | Acuoso | Gas | Acuoso | Gas | Acuoso | |
| T (K) | k (s-1) | |||||
| 365,2 | 4,4 | 1,0×10-2 | 2,4×10-2 | 4,5×10-5 | 5,7×10-6 | 9,0×10-6 |
| 372,2 | 7,3 | 1,9×10-2 | 4,4×10-2 | 9,6×10-5 | ||
| 379,2 | 1,2×101 | 3,5×10-2 | 7,8×10-2 | 2,0×10-4 | ||
| 389,2 | 2,3×101 | 7,9×10-2 | 1,7×10-1 | 5,4×10-4 | ||
| 424,2 | 1,8×102 | 1,0 | 2,1 | 1,2×10-2 | ||
| Ea (kJ.mol-1) | 80,8 | 101,2 | 98,4 | 122,4 | ||
| A (s-1) | 1,6×1012 | 3,0×1012 | 2,7×1012 | 1,5×1013 | ||
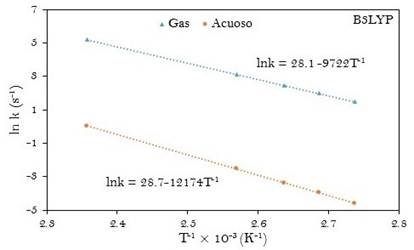
Fig. 4
Gráfica de la ecuación linealizada de Arrhenius para la descomposición del ácido malónico en fase gas y en disolución acuosa. Obtenida a B3LYP/6-31G(d,p)
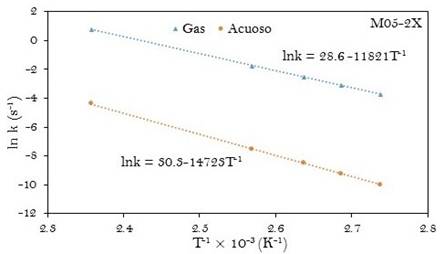
Fig. 5
Gráfica de la ecuación linealizada de Arrhenius para la descomposición del ácido malónico en fase gas y en disolución acuosa. Obtenida a M05-2X/6-31+G(d,p)
Cálculos de NBO
NBO es una técnica de partición poblacional que permite asociar cargas eléctricas a los átomos de las moléculas y también permite obtener los índices de enlace de Wiberg (βi), correspondientes a cada uno de los enlaces involucrados en la reacción química, para cada una de las estructuras del reaccionante, el estado de transición y los productos.
A partir de los βi es posible realizar un amplio seguimiento a los procesos de formación y rompimiento de enlaces durante la reacción. Por ejemplo, la variación relativa del índice de enlace 44, definida como:
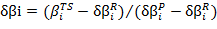 [1]
[1]
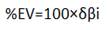 [2]
[2]Dan una idea del grado de avance de los enlaces durante el proceso de reacción.
La tabla 4 presenta los βi para la reacción de descomposición térmica del ácido malónico. Se obtuvieron a M05-2X/6-31+G(d,p) para el mecanismo de reacción 1b, en fase gaseosa y en disolución acuosa.
En los βi, valores cercanos a la unidad indican la existencia de enlaces simples. Los enlaces dobles se caracterizan por tener un índice con valor alrededor de dos y valores cercanos a cero ocurre en el caso de la ausencia del enlace. De manera similar a la interpretación de los índices de enlace en las estructuras de Lewis.
Los enlaces que presentan mayor avance en el estado de transición para la reacción en fase gaseosa corresponden a los enlaces O5-H6, O1-C2 y H6-O1, con valores de 79,87, 78,37 y 72,51 %, respectivamente. El proceso más lento tiene que ver con la formación del enlace C2-C3 (44,7 %). Según esas observaciones, se podría pensar que la reacción inicia con el movimiento del átomo H6 desde el átomo O5 para unirse con el átomo O1 y que ello provocaría los demás reordenamientos electrónicos.
Si se hace una comparación de los resultados de los índices de enlace de Wiberg entre la reacción en fase gaseosa y en disolución acuosa, se observa para la etapa 1 del mecanismo 1b, que el solvente estabiliza levemente las cargas que se generan por la migración del átomo de hidrógeno. Por ejemplo los enlaces O5-H6 y O1-H6 aumentan en porcentaje de evolución de 79,9 a 80,7 y de 72,5 a 75,2 respectivamente. Por el contrario, los demás enlaces del centro de la reacción disminuyen en su porcentaje de evolución. Se podría pensar que el solvente disminuye la movilidad y disponibilidad de electrones en el estado de transición. En la tabla 5 se muestran las cargas NBO para los átomos involucrados en el centro de la reacción, para el reaccionante y el estado de transición. En la misma tabla se calculó el valor absoluto del cambio en la carga atómica desde el reactivo hasta el estado de transición |Δ(TS-R)carga|. Se encuentra que la diferencia es mayor para las cargas atómicas en la fase gaseosa que en disolución acuosa, lo que estaría en concordancia con lo que se dijo acerca de la función del solvente en la reacción.
La sincronicidad de la reacción (SY) es otro indicador para la reacción, se calcula a partir de los índices de enlace de Wiberg, según la siguiente expresión:
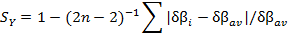 [3]
[3]
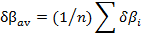 [4]
[4]n, es la cantidad de átomos que participan directamente en la formación y rompimiento de enlaces durante la etapa de la reacción que se esté analizando.
El valor promedio de la variación relativa del índice de enlace (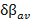 ) permite caracterizar el estado de transición según su posición en el perfil energético de la reacción, de manera similar a lo señalado en el postulado de Hammond.45 El valor de
) permite caracterizar el estado de transición según su posición en el perfil energético de la reacción, de manera similar a lo señalado en el postulado de Hammond.45 El valor de 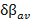 para la reacción estudiada en fase gaseosa es de 0,64, un valor similar fue obtenido para la reacción en disolución acuosa. Según los
para la reacción estudiada en fase gaseosa es de 0,64, un valor similar fue obtenido para la reacción en disolución acuosa. Según los 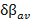 calculados se puede caracterizar el estado de transición TS6b, como una estructura de transición del tipo late, es decir, energética y geométricamente se localiza más cerca a los productos que al reactivo.
calculados se puede caracterizar el estado de transición TS6b, como una estructura de transición del tipo late, es decir, energética y geométricamente se localiza más cerca a los productos que al reactivo.
En teoría, el valor de la sincronicidad está entre los límites de 0 < SY< 1. Un valor de 0 caracterizaría un proceso totalmente asincrónico. Cuando SY es igual a 1, se tendría un proceso de reacción totalmente sincrónico. En términos prácticos, se considera que la reacción transcurre de manera sincrónica cuando el indicador SY presenta un valor comprendido entre 0,9 y 1,0. Según los resultados mostrados en la tabla 4, se puede decir que la reacción estudiada mediante el mecanismo 1b transcurre de forma levemente sincrónica (SY: 0.89 fase gaseosa, 0,88 en disolución acuosa).
| βi | O1-C2 | C2-C3 | C3-C4 | C4-O5 | O5-H6 | H6-O1 |
| R | 1,792 (1,738) | 0,976 (0,984) | 0,973 (0,979) | 1,062 (1,076) | 0,684 (0,672) | 0,000 (0,000) |
| TS | 1,191 (1,196) | 1,344 (1,311) | 0,460 (0,501) | 1,507 (1,502) | 0,138 (0,130) | 0,513 (0,519) |
| P | 1,024 (1,022) | 1,798 (1,794) | 0,000 (0,000) | 1,882 (1,875) | 0,000 (0,000) | 0,708 (0,691) |
| %EVb | 78,37 (75,63) | 44,74 (40,38) | 52,77 (48,83) | 54,26 (53,27) | 79,87 (80,70) | 72,51 (75,17) |
| δβavc | 0,64 (0,62) | |||||
| SYd | 0,89 (0,88) | |||||
El análisis de la tabla 5 permite observar que durante el proceso de la reacción se obtiene un desbalance electrónico debido a un aumento en las cargas negativas de los átomos O1 y C3 y una disminución de la carga positiva en el átomo C2, Mientras tanto los átomos del lado derecho de la estructura reaccionante pierden carga negativa (O5) y ganan carga positiva (átomos C4 y H6).
| Átomo | O1 | C2 | C3 | C4 | O5 | H6 |
| Ácido Malónico | -0,571 (-0,635) | 0,837 (0,862) | -0,701 (-0,710) | 0,840 (0,856) | -0,733 (-0,735) | 0,537 (0,548) |
| TS1 | -0,743 (-0,738) | 0,815 (0,836) | -0,768 (-0,768) | 0,958 (0,964) | -0,713 (-0,730) | 0,577 (0,578) |
| |Δ(TS-R)carga| | 0,172 (0,103) | 0,022 (0,026) | 0,067 (0,058) | 0,118 (0,108) | 0,020 (0,005) | 0,040 (0,030) |
Conclusiones
Se estudió la reacción de descomposición térmica en fase gaseosa y en medio acuoso, mediante dos mecanismos y a dos métodos de cálculo computacional. Energéticamente se encontró que el mecanismo a través de un estado de transición de 6 miembros es favorecido respecto al mecanismo que procede mediante una sola etapa con participación de un estado de transición cíclico de 4 miembros.
Los resultados obtenidos con el método M05-2X/6-31+G(d,p) se ajustan mejor a los resultados experimentales que los resultados obtenidos con el método B3LYP/6-31G(d,p). La reacción transcurre más lenta cuando se lleva a cabo en disolución acuosa que en fase gaseosa.
Los resultados computacionales para la velocidad de conversión desde 1,1-etenediol a ácido acético no están de acuerdo con las observaciones experimentales. El mecanismo por el que ocurre esa etapa de la reacción debe ser diferente al postulado. Los valores obtenidos para 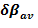 y SY, permiten caracterizar el estado de transición TS6b como una estructura del tipo “late” y el proceso de reacción como levemente sincrónico.
y SY, permiten caracterizar el estado de transición TS6b como una estructura del tipo “late” y el proceso de reacción como levemente sincrónico.
Agradecimientos
Este trabajo fue realizado gracias al apoyo dado por la Universidad Nacional de Colombia, sede Medellín
Referencias bibliográficas
1. GHOSH DASTIDAR, T.; NETRAVALI, A. N. “Green’ crosslinking of native starches with malonic acid and their properties”. Carbohydr. Polym. 2012, 90 (4), 1620-1628. ISSN 0144-8617
2. APELBLAT, A.; MANZUROLA, E. “Volumetric properties of aqueous solutions of malonic acid”. J. Chem. Thermodyn. 2016, 102, 63-67. ISSN 0021-9614
3. MASENDE, Z.; KUSTER, B.; PTASINSKI, K.; JANSSEN, F.; KATIMA, J.; SCHOUTEN, J. “Kinetics of malonic acid degradation in aqueous phase over Pt/graphite catalyst”. Appl. Catal. B Environ. 2005, 56 (3), 189-199. ISSN 0926-3373
4. WAKIL, J. S. “A malonic acid derivative as an intermediate in fatty acid synthesis”. J. Am. Chem. Soc. 1958, 80 (23), 6465-6465. ISSN 0002-7863
5. VELLIS, De J.; SHANNON, L. M.; LEW, J. Y. “Malonic acid biosynthesis in bush bean roots. I. evidence for oxaloacetate as immediate precursor”. Plant Physiol., 1963, 38 (6), 686-690. ISSN 1532-2548
6. KIM, Y. “Malonate metabolism: biochemistry, molecular biology, physiology, and industrial application”. J. Biochem. Mol. Biol. 2002, 35 (5), 443-451. ISSN 1225-8687
7. AMBATI, C.; YUAN, F.; ABU ELHEIGA, L.; ZHANG, Y.; SHETTY, V. “Identification and quantitation of malonic acid biomarkers of In-born error metabolism by targeted metabolomics”. J. Am. Soc. Mass Spectrom. 2017, 28 (5), 929-938. ISSN 1044-0305
8. HINSHELWOOD, C. “XX.-The Rate of Decomposition of Malonic Acid”. J. Chem. Soc. Trans, 1920, 117 (1), 156-165. ISSN 0368-1645
9. EL AWAD, A.; MAHFOUZ, R. “Kinetic analysis of isothermal, non-isothermal and catalysed termal Decomposition of Malonic Acid”. J. Therm. Anal. 1989, 35, 1413-1414. ISSN 1388-6150
10. CAO, J. R.; BACK, R. A. “The thermolysis and photolysis of malonic acid in the gas phase”. Can. J. Chem. 1986, 64 (5), 967-968. ISSN 0008-4042
11. HALL, G. A. “The kinetics of the decomposition of malonic acid in aqueous solution”. J. Am. Chem. Soc. 1949, 71 (8), 2691-2693. ISSN 0002-7863
12. CRUZ CASTAÑEDA, J.; NEGRÓN MENDOZA, A.; FRÍAS, D.; COLÍN GARCÍA, M.; HEREDIA, A.; RAMOS BERNAL, S.; VILLAFAÑE BARAJAS, S. “Chemical evolution studies: the radiolysis and thermal decomposition of malonic acid”. J. Radioanal. Nucl. Chem. 2015, 304 (1), 219-225. ISSN 0236-5731
13. CLARK, L. W. “A systematic study of the kinetics of the decomposition of malonic acid in non-aqueous solvents”. J. Phys. Chem. 1958, 62 (1), 79-81. ISSN 0022-3654
14. MIDYANA, G. G.; MAKITRA, R. G.; PAL’CHIKOVA, E. Y. “Solvent effect on the reaction of decarboxylation of malonic acid. Correlation analysis”. Russ. J. Gen. Chem. 2010, 80 (5), 944-947. ISSN 1070-3632
15. CAIRES, F. J.; GOMES, D. J. C.; GIGANTE, A. C.; LIMA, L. S.; CARVALHO, C. T.; IONASHIRO, M. “Thermal behavior of malonic acid, sodium malonate and its compounds with some bivalent transition metal ions in dynamic N2 and CO2 atmospheres”. Braz. J. Therm. Anal. 2013, 2 (1), 12-16. ISSN 2316-9842
16. STANFORD, V. L.;VYAZOVKIN, S. “Thermal decomposition kinetics of malonicacid in the condensed phase”. Ind. Eng. Chem. Res. 2017, 56 (28), 7964-7970. ISSN 0888-5885
17. LOUDON, A. G.; MACCOLL, A.; SMITH, D. “Heavy atom kinetic isotope effects. Part 1 .-liquid phase decarboxylation of malonic acid”. J. Chem. Soc. Faraday Trans. 1. 1972, 69(1), 894-898. ISSN 0956-5000
18. HUANG, C. L.; WU, C. C.;LIEN, M. H. “Ab initio studies of decarboxylations of the β-keto carboxylic acids XCOCH2COOH (X = H, OH, and CH3)”. J. Phys. Chem. A. 1997, 101 (42), 7867-7873. ISSN 1089-5639
19. DMITRIEVA, N.; GRIDCHIN, S.; ROMODANOVSKII, P.; MAIOROV, A. “Standard enthalpies of formation of D,L-α-alanyl-glycine and the products of its dissociation in aqueous solutions”. Russ. J. Phys. Chem. A. 2010, 84 (11), 1997-1999. ISSN 0036-0244
20. FRISCH, M. J.; et. al. “Gaussian 09, Revision B.01.”. Gaussian, Inc., Wallingford CT, 2010.
21. LEE, C.; YANG, W.; PARR, R. G. “Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density” Phys. Rev. B, 1988, 37 (2), 785-789. ISSN 1098-0121
22. BECKE, A. D. “Density-functional thermochemistry. III. The role of exact exchange” J. Chem. Phys., 1993, 98 (7), 5648-5652. ISSN 0021-9606
23. STEPHENS, P. J.; DEVLIN, F. J.; CHABALOWSKI, C. F.; FRISCH, M. J. “Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields” J. Phys. Chem., 1994, 98 (45), 11623-11627. ISSN 0022-3654
24. ZHAO, Y.; SCHULTZ, N. E.; TRUHLAR, D. G. “Design of density functionals by combining the method of constraint satisfaction with parametrization for thermochemistry, thermochemical kinetics, and noncovalent interactions” J. Chem. Theory Comp., 2006, 2 (2), 364-382. ISSN 1549-9618
25. DITCHFIELD, R.; HEHRE, W. J.; POPLE, J. “Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules” J. Chem. Phys., 1971, 54, 724-728. ISSN 0021-9606
26. MERRICK, J. P.; MORAN, D.; RADOM, L. “An evaluation of harmonic vibrational frequency scale factors” J. Phys. Chem. A, 2007, 111 (45), 11683-11700. ISSN 1089-5639
27. MCQUARRIE, D.; SIMON, J.Molecular Thermodynamics. Sausalito: University Science Books, 1999.ISBN 1-891389-05-X
28. TOMASI, J.; MENNUCCI, B.; CAMMI, R. “Quantum mechanical continuum solvation models” Chem. Rev., 2005, 105 (8), 2999-3093. ISSN 0009-2665
29. GLASSTONE, K.; LAIDLER, K.; EYRING, H.The Theory of Rate Processes. New York: McGraw-Hill, 1941. ISBN 0070233608
30. BENSON, S. The Foundations of Chemical Kinetics. New York: McGraw-Hill , 1960. ISBN 0070047782
31. FUKUI, K. “A formulation of the reaction coordinate” J. Phys. Chem., 1970, 74 (23), 4161-4163. ISSN 0022-3654
32. REED, A. E.; WEINHOLD, F. “Natural bond orbital analysis of nearHartree - Fock water dimer” J. Chem. Phys., 1983, 78, 4066-4073. ISSN 0021-9606
33. REED, A. E.; CURTISS, L. A.; WEINHOLD, F. “Intermolecular interactions from a natural bond orbital , donor-acceptor viewpoint” Chem. Rev., 1988, 88, 899-926. ISSN 0009-2665
34. GLENDENING, E. D.; BADENHOOP,J. K.;REED, A.E.; CARPENTER, J.E.; MORALES, C.E.; WEINHOLD, F. “NBO 5.0” Theoretical Chemistry Institute, University of Wisconsin, Madison, 2001
35. WIBERG, K. B. “Application of the Pople-Santry-Segal CNDO method to the ciclopropylcarbinyl and cyclobutyl cation and to bicyclobutane” Tetrahedron, 1968, 24, 1083-1096. ISSN 0040-4020
36. GAO, J.“A theoretical investigation of the enol content of acetic acid and the acetate ion in aqueous solution” J. Mol. Struct. THEOCHEM, 1996, 370, 203-208. ISSN 0166-1280
37. LAURELLA, S.β-cetoamidas : estudio de equilibrios tautoméricos y reactividad química.Tesis Doctoral, Universidad Nacional de la Plata, La Plata, 2012.
38. SPENCER, J. N.; HOLMBOE, E.; KIRSHENBAUM, M.; FIRTH, D.; PINTO, P. “Solvent effects on the tautomeric equilibrium of 2,4-pentanedione” Can. J. Chem., 1982, 60, 1178-1182. ISSN 0008-4042
39. DUAN,X.; PAGE, M. "Theoretical investigation of competing mechanisms in the thermal unimolecular decomposition of acetic acid and the hydration reaction of ketene" J. Am. Chem.Soc ., 1995,117, 5114-5119. ISSN 0002-7863
40. FREY, J.; RAPPOPORT, Z. “Observation of an amide enol of bis(2,4,6-triisopropylphenyl)acetic acid,” J. Am. Chem. Soc., 1996, 118 (16), 3994-3995. ISSN 0002-7863
41. NGUYEN, T. L.; XUE, B. C.; ELLISON, G. B.; STANTON, J. F. “Theoretical study of reaction of ketene with water in the gas phase: formation of acetic acid?” J. Phys. Chem. A, 2013, 117 (43), 10997-11005. ISSN 1089-5639
42. HEGARTY, A. F.; NGUYEN, M. T. “Molecular orbital study on the hydrolysis of ketene by water dimer: β-carbon vs. oxygen protonation?” J. Am. Chem. Soc., 1984, 106, 1552-1557. ISSN 0002-7863
43. KRESGE, A. “Ingold Lecture. Reactive intermediates: carboxylic acid enols and other unstable species” J. Chem. Soc. Rev., 1996, 25, 275-280. ISSN 0306-0012
44. MOYANO, A.; PERICAS, M.; VALENTÍ, E. “A theoretical study on the mechanism of the thermal and the acid-catalyzed decarboxylation of 2-oxetanones (β-Lactones)” J. Org. Chem., 1989, 54 (3), 573-582. ISSN 0022-3263
45. HAMMOND,G. “A Correlation of Reaction Rates” J. Am. Chem. Soc., 1955, 77 (2), 334-338. ISSN 0002-7863
Notas de autor
*Autor para la correspondencia. correo electrónico:paruizr@unal.edu.co