Sólidos de Revolução num Curso de Engenharia com Matlab
Revolution Solids in Engineering Course with Matlab
Sólidos de Revolução num Curso de Engenharia com Matlab
Research, Society and Development, vol. 4, núm. 2, pp. 102-115, 2017
Universidade Federal de Itajubá

Este trabalho está sob uma Licença Internacional Creative Commons Atribuição 4.0.
Recepção: 10 Outubro 2016
Aprovação: 11 Janeiro 2017
Resumo: Este trabalho tem por finalidade apresentar duas atividades elaboradas com o software Matlab sobre o ensino dos conceitos matemáticos de Sólido de Revolução nos Eixos x e y, usadas como ferramenta de apoio pedagógico com alunos de um curso de Engenharia, complementando as aulas expositivas presenciais sobre esse mesmo tema. A metodologia utilizada é do tipo acadêmico, buscando ampliar o conhecimento na disciplina Cálculo Diferencial e Integral quanto ao processo de ensino-aprendizagem. Pelos resultados obtidos podemos comprovar a importância da utilização de tal ferramenta no processo de ensino-aprendizagem uma vez que a aula tornou-se um momento diferenciado, pela interação e motivação do aluno, que participa ativamente de seu aprendizado com aproveitamento melhor ou superior ao da aula expositiva.
Palavras-chave: Sólidos de Revolução, Software Matlab, Engenharia.
Abstract: This paper aims to present two activities elaborated with the Matlab software on the teaching of Mathematical concepts of Solid of Revolution in the x and y axes, used as pedagogical support tool with students of an Engineering course, complementing the expositive classes on the same subject . The methodology used is of the academic type, seeking to extend the knowledge in the discipline Differential and Integral Calculus regarding the teaching-learning process. Based on the results obtained, we can prove the importance of the use of such a tool in the teaching-learning process because the classroom became a differentiated moment, through the interaction and motivation of the student, who actively participates in his or her learning with better or better use of the lecture .
Keywords: Revolution Solids, Matlab Software, Engineering.
1. Introdução
Há pesquisas que evidenciam preocupações de educadores relacionadas ao ensino-aprendizagem de matemática, em diversos níveis do ensino, destacando-se, sobretudo as dificuldades dos alunos em Análise e Cálculo Diferencial e Integral.
Muitos fatores podem estar relacionados a essas dificuldades encontradas pelos alunos, principalmente quando ingressam no ensino superior. Podemos mencionar, por exemplo, que os alunos possuem deficiências em conhecimentos de matemática básica, de leitura e interpretação de textos, na resolução de problemas e na capacidade de argumentação. Alguns estudos revelam resultados de testes realizados com alunos de vários níveis, evidenciando que os mesmos não têm domínio em conteúdos de Álgebra e Geometria do Ensino Fundamental, como também em Trigonometria e Geometria Espacial do Ensino Médio. Em consequência, já no ensino superior, o índice de reprovação aumenta pelo baixo rendimento desses alunos e, novamente, há evasão nessas disciplinas e na universidade.
Segundo Costa e Hartmann (2011):
‘As principais dificuldades dos alunos mostram-se no desconhecimento da matemática básica necessária em cálculo como, por exemplo, a compreensão do que é uma função, fatoração, dúvidas de como igualar os denominadores para resolver a soma de uma fração, divisão entre duas frações, desenvolvimento de um produto notável, entre outras situações. Também se observou a dificuldade que os alunos demonstram em explicar suas idéias, justificar os procedimentos adotados na resolução dos exercícios, argumentar e contra argumentar.’
A Comissão Especial de Estudos sobre a Evasão nas Universidades Públicas Brasileiras definiu em seu estudo três fatores que influenciam a evasão universitária, sendo eles: fatores referentes às características individuais do estudante, fatores internos às instituições e fatores externos às instituições. Os fatores referentes às características individuais do estudante têm relação com habilidades de estudo, personalidade, formação escolar de níveis anteriores, escolha precoce da profissão, dificuldades de adaptação à rotina universitária, falta de compatibilidade entre a vida acadêmica e as exigências do mercado de trabalho, desencanto pelo curso resultando em desmotivação, dificuldade na relação ensino-aprendizagem, reprovações sucessivas e desinformação acerca da natureza dos cursos (ANDIFES/ABRUEM/SESu/MEC,1996).
O estudo das dificuldades que o estudante encontra para sua permanência na faculdade é de extrema importância, uma vez que o alto índice de evasão na universidade pode causar um grande impacto social, visto a falta de mão de obra qualificada em determinadas áreas.
Segundo Morais,
Acreditamos que o abandono dos estudantes da universidade pode ser um dos fatores que contribuem para a desigualdade social, visto que o mercado de trabalho se encontra cada dia mais exigente em busca de profissionais qualificados para exercerem as mais variadas funções, o que dificulta quando o candidato não se enquadra neste padrão (MORAIS, 2015).
Nesse contexto, estamos interessados em superar/amenizar algumas das dificuldades com relação às características individuais do estudante, em particular sobre lacunas matemáticas de ensinos anteriores. Para tal, o que temos feito é integrar o uso de tecnologias, tais como as calculadoras científicas e os softwares, ao ambiente da sala de aula presencial. Entendemos que o ensino-aprendizagem não pode mais ser visto como uma simples transmissão e recepção de informações, sendo necessário então variar as estratégias ou técnicas empregadas no ensino visando atender às diferenças próprias de cada aluno.
A cada dia um novo software surge no ambiente estudantil, livre ou gratuito, que pode auxiliar nesse processo de aprendizagem e de construção do conhecimento.
Valente (2008) afirma que a escola deveria incorporar cada vez mais a utilização das tecnologias digitais, para que seus estudantes pudessem aprender a ler, escrever e se expressar por meio desses instrumentos. Ao integrar tecnologias ao processo de ensino-aprendizagem, surge um excelente caminho para promover novos conhecimentos que permitem a inserção dos estudantes num contexto social e tecnológico.
Em Parâmetros Curriculares Nacionais, podemos ler:
[...] Quanto aos softwares educacionais é fundamental que o professor aprenda a escolhê-los em função dos objetivos que pretende atingir e de sua própria concepção de conhecimento e de aprendizagem, distinguindo os que se prestam mais a um trabalho dirigido para testar conhecimentos dos que procuram levar o aluno a interagir com o programa de forma a construir conhecimento (PCN, 1997).
Sob esse enfoque, buscando sanar algumas lacunas matemáticas que, possivelmente, os alunos apresentam, bem como levando em conta nossa experiência docente que revela dificuldades dos alunos em certos temas matemáticos, apresentamos duas atividades elaboradas por meio de um software, abordando os temas Área e Volume de sólido de revolução em torno dos eixos x e y.
Sem dúvida, calcular a área e o volume de um objeto é um tema importante, que faz parte da grade curricular num curso de Engenharia, pois a partir desses conceitos é possível estimar os custos de fabricação de um objeto. Isso significa que a partir da forma geométrica de um objeto é possível determinar a quantidade de material a ser usado, determinar o tempo necessário gasto e os melhores processos de fabricação, ou ainda o custo para submeter esse componente a um tratamento superficial. Lembrando-se ainda que, para ARBACHE (2011), ‘o cálculo de volume de um componente mecânico também é muito utilizado para determinar os custos de operações de transporte e armazenagem do mesmo’.
Há muitos softwares, pagos ou gratuitos, que podem ser utilizados como ferramenta auxiliar no ensino-aprendizagem de matemática, e que constatamos em nossa experiência com alunos de engenharia, ser benéfico em amenizar as dificuldades encontradas pelos mesmos ao estudar Área e Volume de sólido de revolução.
No presente trabalho, temos particular interesse no Matlab. Trata-se de um software de alta performance cujo elemento básico de informação é uma matriz. Justificamos a nossa escolha pelo Matlab tendo em vista que a Universidade, na qual lecionamos, possui licença do mesmo para diversos computadores e, sobretudo, porque o aluno fará uso desse software em outras disciplinas no decorrer de seu curso de engenharia. Além disso, também é oportuno salientar que gráficos de sólidos de revolução, em geral, não são feitos em sala de aula presencial em nossa Universidade e, por isso, são propostos em trabalhos extra classe durante a disciplina em curso.
Essas Atividades, bem como o software Matlab são descritos nos próximos itens.
2. Software Matlab*
Matlab (MATrix LABoratory) é um software de alta performance que integra análise numérica, cálculo com matrizes, processamento de sinais e construção de gráficos em ambiente fácil de usar, em que problemas e soluções são expressos somente como são escritos matematicamente, ao contrário da programação tradicional *.
É um sistema interativo cujo elemento básico de informação é uma matriz, que não requer dimensionamento. Esse software permite a resolução de muitos problemas numéricos em apenas uma fração do tempo, diferente do que se gastaria para escrever um programa semelhante em linguagem Fortran, Basic ou C. Além disso, as soluções dos problemas são expressas quase que exatamente igual ao que elas são escritas matematicamente num papel.
Foi criado no fim dos anos 70 por Cleve Moler, então presidente do departamento de ciência da computação da Universidade do Novo México.
Matlab logo se espalhou para outras universidades e encontrou um amplo uso no âmbito da comunidade matemática aplicada. O engenheiro Jack Little conheceu a linguagem Matlab, durante uma visita feita por Moler a Universidade de Stanford em 1983. Reconhecendo o seu potencial comercial, ele juntou-se a Moler e Steve Bangert. Reescreveram o Matlab em linguagem C, em 1984 fundaram a MathWorks, prosseguindo em seu desenvolvimento.
Matlab foi adotado pela primeira vez por engenheiros de projeto de controle, a especialidade de Little, e rapidamente se espalhou para outros campos de aplicação. Atualmente é também utilizado nas áreas de educação, em especial no ensino da álgebra linear e análise numérica, e é muito popular entre os pesquisadores envolvidos com o processamento de imagem.
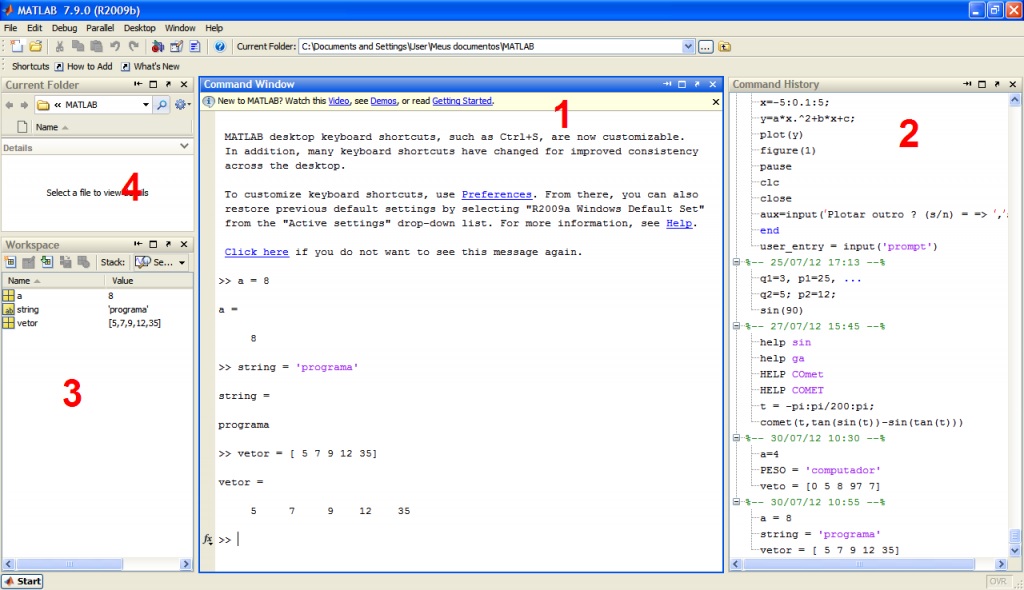
Para executar o Matlab (previamente instalado no computador) em ambiente Windows, deve-se colocar o cursor sobre seu ícone e pressionar com o botão esquerdo do mouse, aparecendo então a janela de comando na qual o usuário e o Matlab interagem. O sinal >> significa que Matlab está pronto para receber os comandos digitados pelo usuário. Ao ser carregado, nos deparamos com algumas janelas, que são as seguintes:
-
1 – Command Window: Essa janela é o local onde são digitados os comandos e operações.
-
2 – Command History: Nessa janela é possível ver todos os comandos e dados apresentados ao programa.
-
3 – Workspace: Espaço onde é possível visualizar as variáveis que já se trabalhou.
-
4 – Current Folder: Lugar onde é possível encontrar o arquivo no formato .m
O Matlab também dispõe de uma janela chamada Editor. Nela podemos criar nossos programas e salvá-los na extensão .m. É possível acessar esse espaço através de File> New> Script, File>New>M-file ou Ctrl+N.
Para trabalhar na janela Command Window, escrevemos os comandos após o símbolo >> , e nesse espaço podemos continuar digitando até o momento em que apertamos a tecla ENTER. Contudo, nessa janela não é possível fazer correções de digitação a não ser digitando-as novamente. Na janela Editor, as correções são possíveis a qualquer momento o que facilita muito a sistematização de um problema a ser resolvido.
Algumas operações básicas, que seguem a ordem matemática de predominância, são apresentadas no Quadro 1, seguinte:
| Operação básica | Símbolo | Exemplo |
| Soma | + | 3+5 |
| Subtração | – | 90-45 |
| Multiplicação | * | 3*6 |
| Divisão | / ou \ | 16/4 |
| Potência ( ) | ^ | 4^3 |
Quando colocamos certa operação no espaço determinado e apertamos a tecla ENTER, obtemos o resultado numa variável chamada ans (answer). Porém, também podemos criar uma variável, igualando-a as operações e a variável através do símbolo =. Por exemplo, ao digitarmos 2^3 obtemos a resposta ans=8 ou então para m=2^3 obtemos a resposta m=8 .
Existem também outros símbolos comuns no uso do Matlab. A tabela abaixo mostra quais são e suas funções:
| Símbolo | Função |
| , | Permite separar diversas variáveis somente numa linha. |
| ; | Suprime da tela a informação daquela variável que está antes do ponto e vírgula, porém ela é ainda salva como variável. |
| % | Tudo que está depois desse símbolo é entendido pelo código como comentário e não será processado. |
| … | Caso necessite pular uma linha, é necessário o uso das reticências. |
O software possui muitas maneiras convenientes para a criação de matrizes de várias dimensões. No vocabulário do Matlab, por exemplo, um vetor refere-se a uma dimensão (1 × N ou N × 1), comumente referida como um vetor em outras linguagens de programação. A matriz geralmente refere-se a uma matriz multidimensional, isto é, uma matriz com mais de uma dimensão, por exemplo, uma matriz do tipo N × M ou uma N × M × L, onde N, M, L, são superiores a 1. Matlab permite definir de maneira simples uma arrays, usando a sintaxe dada por inicial: incremento: final.
Matlab é uma combinação perfeita de muitas das linguagens mais utilizadas, tais como C, Java e Basic. Essa linguagem segue então, de uma maneira muito fiel, a maior parte dos aspectos das linguagens de sua origem. Isso é uma das grandes vantagens do Matlab, pois um programador de C não terá grandes dificuldades em se adaptar a esta nova linguagem, visto que os códigos-fonte são muito parecidos. Também um programador de Java não encontrará dificuldade em se adaptar à construção de objetos GUI em Matlab.
O programa dispõe de diversas extensões, chamadas toolboxes ou blocksets.
Além desses módulos adicionais, o Matlab conta com o Simulink, um ambiente de simulação baseado em diagrama de blocos e plataforma para Model-Based Design, muito usado em engenharia.
O Matlab conta ainda com o MuPAD (Multi-Processing Algebra Data Tool), que é um sistema de computação algébrica (C.A.S. – Computer Algebra System) interativo, desenvolvido à partir de 1990 na Universidade de Paderborn (Alemanha) com todos os recursos dos principais softwares comerciais nesta área.
No MuPAD é possível solucionar praticamente todos os tipos de problemas de matemática, podendo ser usado como um programa stand-alone. Ainda está disponível em Symbolic Math Toolbox do Matlab, mas nas próximas edições (release) será substituído pelo Windows Live (mais informações pode-se consultar https://www.mathworks.com/products/matlab.html ).
Há muito que falar sobre os estudos e usos desse software na área educacional, todavia foge ao escopo do presente texto, deixando para próximos trabalhos. Para mais detalhes sobre Matlab pode-se consultar o endereço http://es.mathworks.com/matlabcentral/.
No que se segue, apresentamos as duas atividades elaboradas no Matlab sobre Área e Volume de Sólido de Revolução em torno dos Eixos x e y. Para tal, a metodologia utilizada, de natureza acadêmica, buscou ampliar e diversificar as tratativas adotadas na disciplina Cálculo Diferencial e Integral quanto ensino e a aprendizagem.
3. Usando o Matlab com Sólido de Revolução
Superfícies e sólidos de revolução são amplamente usados em design industrial, arquitetura, engenharias e são importantíssimos quando se trata, por exemplo, em estimar custos de fabricação.
Em geral, dizemos uma superfície de revolução quando ela é oca, enquanto que um sólido de revolução é maciço.
Resumidamente falando, um sólido de revolução é um sólido gerado pela rotação de uma região plana em torno de uma reta que está no mesmo plano da região. Nesse caso, a reta é denominada eixo de revolução. Muitos sólidos conhecidos são desse tipo.
Para os cálculos de área e de volume do sólido, consideramos que a curva faz uma revolução em torno de um eixo fixo, podendo ser o eixo x, o eixo y ou, um outro, pré-determinado.
Na Atividade 1, a seguir, queremos determinar a área do sólido gerado pela rotação em torno do eixo X. Nesse caso, lembramos que a fórmula que permite calcular a área é dada por ,
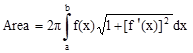
, onde f(x) e o intervalo [a, b] são dados.
Além disso, para visualizar o sólido de revolução, temos que fazer o gráfico e para tal precisamos ainda de parametrização. Isso é obtido através das seguintes equações*
Dada y=f(x), (sob certas condições) as parametrizações são as seguintes:
-
Eixo X Þ F(u,v)=u ; G(u,v)= f(u).cos(v) ; H(u,v)=f(u).sin(v)
-
Eixo Y Þ F(u,v)= u.cos(v) ; G(u,v)=f(u) ; H(u,v)=u.sin(v)
Assim, a Atividade 1, proposta para o aluno, tem o seguinte enunciado:
Atividade 1: Determinar a área do sólido gerado pela rotação em torno do Eixo X, considerando a curva y=f(x)=x3 , com 0≤x≤4 .
A resolução, a mão e no papel, é a seguinte:
Como f(x)=x3 então f ’(x)=3x2. Daí, temos a integranda
Então:
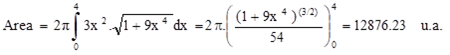
A resolução no Matlab é dada abaixo:
Podemos fazer a digitação no Comannd Window ou no Editor. Aqui optamos pelo Editor para resumir a tela de resolução. Usamos também a opção Publish para obter a seguinte resolução em formato .doc.


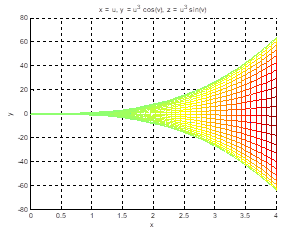
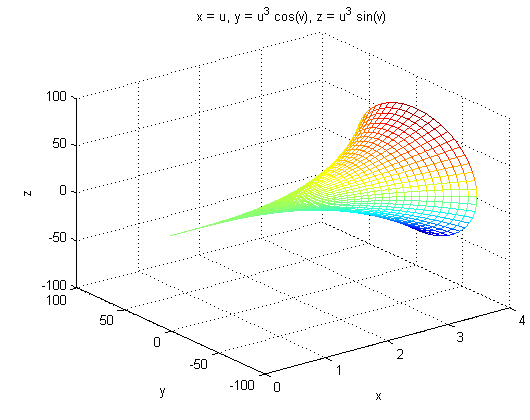
Esclarecemos, ainda, que o Matlab possui um ícone/ferramenta que permite girar/rodar as figuras acima, obtendo outros ângulos de visão.
Atividade 2: Determinar o volume do sólido gerado pela rotação em torno do eixo y da região plana delimitada pelas curvas
por y=2 e por x=0 .
A resolução, a mão e no papel, é a seguinte:
Como
e x=0 então y=6.
Lembrando a fórmula
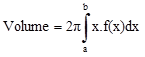
então
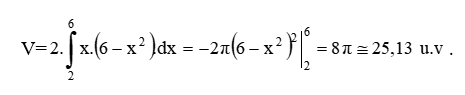
No Matlab optamos, novamente, pela digitação no Editor e usamos ainda a opção Publish para obter a resolução em formato .doc.
A resolução no Matlab é a seguinte:
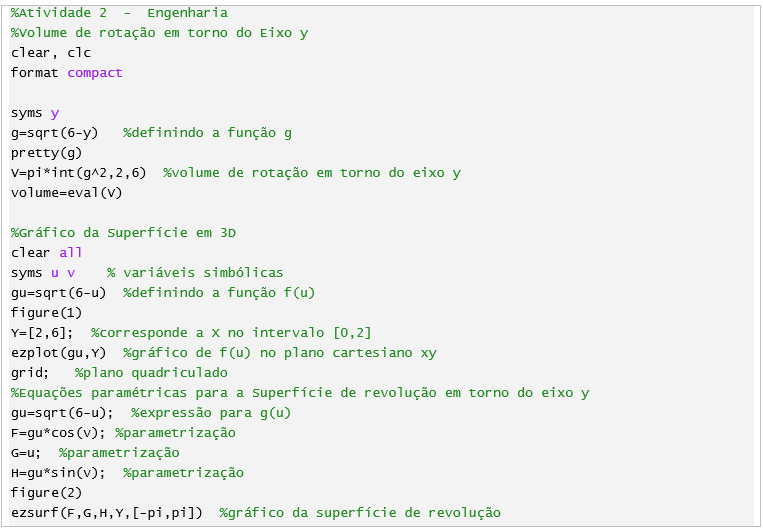
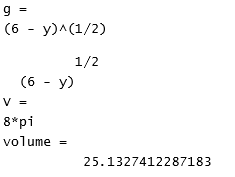
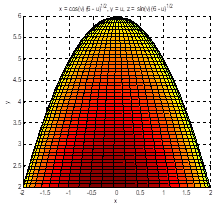
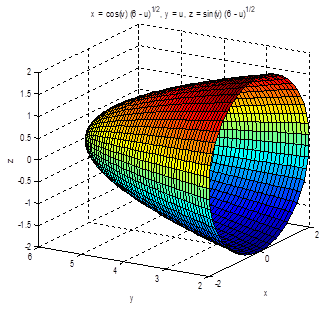
Elaboramos também mais 2 Atividades, sendo uma sobre Área do sólido gerado pela rotação em torno do Eixo Y e a outra sobre Volume do sólido gerado pela rotação em torno do Eixo X, cujas soluções são análogas as que apresentamos aqui, deixando para os alunos fazerem as resoluções. Salientamos, novamente, que gráficos de sólidos de revolução são propostos em trabalhos extra classe durante a disciplina em curso da Universidade.
4. Considerações Finais
Como educadores, preocupados com o ensino e a aprendizagem de matemática, em especial no que se refere às dificuldades dos alunos em Análise e Cálculo Diferencial e Integral, podemos fazer uso de certos softwares que permitem tornar as aulas um momento diferenciado, pela interação do aluno ao participar ativamente de seu aprendizado com aproveitamento melhor ou superior ao da aula expositiva.
Entendemos que é possível renovar e criar condições para que os alunos possam participar de todo o seu processo de aprendizagem. Para tal, para que a aprendizagem seja realmente efetiva é necessário que o aluno tenha vontade de aprender, que busque continuamente a compreensão e procure novas soluções, participando ativamente na construção de seu próprio conhecimento.
Por outro lado, para que isso seja possível, o professor precisa estar disposto a encontrar formas de inovar no ensino o conteúdo convencional, transpondo o espaço escolar, navegando pela Internet e expandindo o conhecimento de seus alunos.
Em nossa experiência docente, ao propor essas atividades para os alunos de um curso de Engenharia, constatamos que foi importante a inserção dessa nova proposta metodológica usando o software Matlab no ensino, já que permitiram lidar com o conceito de Sólido de Revolução de uma forma significativa e estimulante para os alunos.
Isso nos revelou, mais uma vez, que o emprego da tecnologia na educação modifica a forma de ensinar e, sobretudo, a forma de aprender. Modifica, principalmente, o conceito de curso, de aula, de professor e de aluno num ambiente universitário.
Na verdade o que precisamos modificar é a nossa prática educativa, buscando sempre o conhecimento a cada dia. Foi o que procuramos fazer, em nossas tarefas docentes, pois ao lidar com o software Matlab tornamos a aula um momento diferenciado para o aluno, através de sua interação e motivação.
Sabemos que há muitos outros trabalhos que enfatizam as pesquisas sobre o potencial dos recursos tecnológicos para o ensino. Como há também diversos temas matemáticos que podem ser abordados pelo software Matlab, em vários momentos do curso superior, que futuramente pretendemos estudar e propor aos alunos.
Esperamos de alguma forma ter contribuído com as discussões acerca desse tema, especialmente no ensino de matemática na engenharia, visando à aprendizagem.
Concluímos com a afirmação de Vilardell (2000): ‘O melhor resultado não virá pela tecnologia, mas pela compreensão do que se espera da educação’.
Referências
ANDIFES/ABRUEM/SESu/MEC. Diplomação, Retenção e Evasão nos Cursos de Graduação em Instituições de Ensino Superior Públicas. Comissão Especial de Estudos sobre a Evasão nas Universidades Públicas Brasileiras, 1996.
BOERI, C.N. e VIONE, M.T.. Abordagens Em Educação Matemática. disponível em http://www.dominiopublico.gov.br/download/texto/ea000661.pdf. Acessado em 15 dezembro 2016.
BRASIL. Ministério da Educação e do Desporto. Secretaria de Educação Fundamental. (2002) Parâmetros Curriculares Nacionais: Matemática. Brasília: MEC/SEF.
COSTA, V.H.H. e HARTMANN, A.M.. Anais do Salão Internacional de Ensino, Pesquisa e Extensão, 2011. Disponível em http://seer.unipampa.edu.br/index.php/siepe/article/view/2819
JARDIM, D.F. et al. Softwares matemáticos na construção de novos perfis sócio- educacionais. In: SINTEGRA, v.1,p.422, 2012b, UFVJM, Anais do I Sintegra, Diamantina- MG, Disponível em http://sintegra.ufvjm.edu.br/arquivos/docs/AnaisSINTEGRA2012.pdf Acessado em 15 Dez. 2016.
KABACA, T. AKTUMEN, M.. Using the Geogebra as an Expressive Modeling Tool: disconvering the anatomy of Cycloids parametric equation. In: First Eurasia Meeting of Geogebra, 2010.
MATLAB. MATLAB Central - MathWorks disponível em <https://es.mathworks.com/matlabcentral>. Acessado em 15 Dez. 2016.
MORAIS, K.S.. A dificuldade do ingressante no Ensino Superior. Website Brasil Escola 2010. Disponível em:<http://meuartigo.brasilescola.uol.com.br/psicologia/a-dificuldade-ingressante-no-ensino-superior-para-htm> . Acesso em 15 Dez. 2016.
MORAN, J. M., MASETTO, M.T., BEHRENS, M.A. Novas tecnologias e mediação pedagógica. Campinas, SP: Papirus, 5ª ed., 2002.
PERRENOUD, P. Dez novas competências para ensinar. Artmed, 2000.
PIVA, C. et al. Articulação entre álgebra e geometria de sistemas lineares em ambiente informatizado: uma experiência em curso de engenharia. In: CONGRESSO INTERNACIONAL DE MATEMÁTICA, ENGENHARIA E SOCIEDADE – ICMES 2009, 1, 2009a, Curitiba.
PONTE, J.P., BROCARDO, J., OLIVEIRA, H. Investigações matemáticas na sala de aula. 2. ed. Belo Horizonte: Autêntica, 2009.
SCHLIEMANN, A. L. D. CARRAHER, D. W. CARRAHER, T. N., 2001. Na vida dez, na escola zero. 11ª Edição. São Paulo. Cortez Editora.
SOUSA, G. C. de; AMORIM, F. V.; SALAZAR, J. V... Atividades com GeoGebra para o Ensino de Cálculo (TA). In: XIII CONFERÊNCIA INTERAMERICANA DE EDUCAÇÃO MATEMÁTICA. 2011.
TARDIF, M. Saberes docentes e formação profissional. 15. ed. Petrópolis: Vozes, 2013.
VALENTE, J. A.. Integração Currículo e Tecnologia e a produção de narrativas. (2012). Currículo sem Fronteiras. Campinas-SP . v. 12, n. 3, p. 57-82, Set/Dez 2012. Disponível em: http://www.curriculosemfronteiras.org/vol12iss3articles/almeida-valente.htm. Acessado em 5 junho de 2016.
VILARDELL, N. P. C.. Novas Linguagens, Novas Oportunidades, Novas Formas De Ensinar E Aprender. Disponível em http://www.academia.edu/10987348. Acessado em 21 setembro de 2015.
Notas