Estudio comparativo inferencial de esfuerzo flexionante en engranes rectos aplicando análisis teórico e Ingeniería Asistida por Computadora
Inferential Statistics Comparative Study of Bending Stress in Spur Gears Applying Theoretical Analysis and Computer-Aided Engineering
Estudio comparativo inferencial de esfuerzo flexionante en engranes rectos aplicando análisis teórico e Ingeniería Asistida por Computadora
Científica, vol. 20, núm. 2, pp. 103-109, 2016
Instituto Politécnico Nacional
Recepción: 13/10/2015
Aprobación: 08/03/2016
Resumen: El análisis teórico de esfuerzo flexionante en engranes rectos aún depende de la aplicación de la fórmula de Lewis en conjunto con factores de corrección, cuya selección, se realiza con base en fórmulas y en la experiencia del diseñador. Sin embargo, en la actualidad, la Ingeniería Asistida por Computadora (CAE) ha evolucionado el estudio de los sistemas mecánicos con nuevas herramientas que permiten realizar y validar el análisis a través de métodos numéricos. No obstante, siempre existe la incertidumbre sobre qué método es más apropiado y preciso. El objetivo fue determinar si existen diferencias significativas en los resultados obtenidos por el análisis teórico y por CAE en el cálculo de esfuerzo flexionante para engranes rectos mediante un análisis comparativo inferencial. La metodología consistió en analizar diez casos diferentes por ambos métodos variando dos parámetros principales: el factor de sobrecarga y el tamaño del mallado. Posteriormente, se realizó un análisis de varianza y la prueba de Tukey para identificar las diferencias. Los resultados revelaron diferencias significativas ( p <0.05) cuando se aplica un factor de sobrecarga alto o un mallado medio, por lo que se concluye que en casos de factores moderados y mallado fino la aplicación de ambos métodos es apropiada.
Palabras clave: esfuerzo flexionante, engranes rectos, análisis comparativo, ingeniería asistida por computadora.
Abstract: Theoretical analysis of bending stress in spur gears still depends on the application of the Lewis formula with correction factors. This selection is made based on formulas and experience of the designer. However, at present, the Computer Aided Engineering (CAE) has evolved the study of mechanical systems with new tools that allow the analysis and validation through numerical methods. However, there is always uncertainty about which method is more appropriate and accurate. The aim of this study was to determine whether there are significant differences in the results obtained by the theoretical analysis and CAE in the calculation for bending stress of spur gears by an inferential comparative analysis. The methodology consisted of ten different cases analyzed by both methods varying two main parameters: the overload factor and mesh size. Subsequently, an analysis of variance and Tukey's test was performed to identify the differences. The results revealed significant differences ( p <0.05) when it is applied either a high load factor or average mesh, so it is concluded that in cases of moderate factors and fine mesh, the application of both methods is appropriate.
Keywords: bending stress, spur gears, inferential statistics, Computer-Aided Engineering.
1. Introducción
El diseño teórico de un sistema de engranaje en muchas ocasiones es complejo debido al número de variables, limitaciones y relaciones que se involucran [1]. Sin embargo, su extensa aplicación en la industria hace que su análisis siga siendo pertinente, en la búsqueda de métodos que permitan su estudio de una manera más simple y, al mismo tiempo, confiable [2], lo que conlleva a la consideración de diversos criterios de diseño y teorías de cálculo, ya sea con la filosofía de diseño por evolución como por la de innovación [3].
La teoría clásica de esfuerzo flexionante se fundamenta en la ecuación de Lewis, la cual parte del supuesto de que el diente es como una viga en voladizo cuya sección crítica está en la raíz, sujeta a una carga uniformemente distribuida a lo largo del ancho de la cara del diente [4]. Es claro que cuando un engrane aplica una carga a otro, la carga se desplaza a todo lo largo del diente, iniciando su aplicación en la punta del mismo [5]. Estos principios siguen siendo válidos, pero han sido aumentados con factores adicionales para tomar en consideración mecanismos de falla que a través del tiempo fueron comprendidos, como lo es la concentración de esfuerzos [6]. Actualmente, el análisis teórico es regido por la American Gear Manufacturers Association (AGMA), que presenta un conjunto de normas bien estructuradas de información para el diseño y análisis de sistemas de transmisión por engranes.
Por otra parte, en Ingeniería Mecánica se ha venido desarrollando una nueva área llamada Ingeniería Asistida por Computadora (Computer Aided Engineering, CAE), que es una herramienta para realizar cálculos, estudios y simulaciones de sistemas dinámicos con base en el uso de programas computacionales que permiten el modelado y análisis de piezas, y que se fundamenta en la aplicación del Método del Elemento Finito (MEF). Para tal fin, el modelo se divide en numerosas piezas de formas simples llamadas "elementos" permitiendo su análisis en forma individual. Este proceso de división se conoce como "mallado del modelo", siendo uno de los parámetros que mayor influencia tiene durante el proceso de cálculo [7].
Tanto el análisis teórico como del CAE presentan diferencias, ventajas y desventajas en su aplicación. No obstante, ambos son de gran utilidad para los diseñadores, ya que son una referencia confiable para tomar decisiones. Sin embargo, dependen muchas veces del criterio, conocimientos y habilidades de quién los aplica [8]. Por lo tanto, el objetivo del presente trabajo fue determinar si existen diferencias significativas entre los resultados obtenidos por ambos métodos en el análisis de esfuerzo flexionante en engranes rectos con un nivel de significancia del 95%, a través del estudio de diez casos sometidos a diferentes tipos de carga variando dos parámetros de control principales: el factor de sobrecarga en el análisis teórico y el tamaño de malla en la aplicación de CAE.
2. Desarrollo
El presente trabajo se estructuró en tres etapas de análisis, las cuales, se describen a continuación.
2.1. Análisis teórico
De los métodos más reconocidos para el análisis de esfuerzo flexionante en engranes rectos, se destaca el de la norma AGMA 2001-D04, el cual, presenta un método teórico para diseñar satisfactoriamente un sistema de engranaje de ejes paralelos aplicando una serie de factores adicionales de modificación al esfuerzo flexionante calculado en conjunto con la ecuación de Lewis modificada [9], dando como resultado una mejor estimación del valor real del esfuerzo que se produce en los dientes de los engranes [10]. La ecuación de Lewis considera como variables principales a la fuerza tangencial ( Wt ), el paso diametral ( Pd ), el ancho de la cara del diente ( F ) y el factor de forma de Lewis ( J ) que depende de la geometría del diente. Aunque ya no se aplica en su forma general, sirve como base para la propuesta definida en AGMA 2001-D04, cuya fórmula para calcular el esfuerzo de flexión en los dientes de un engrane recto es [8]:
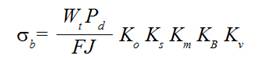 (1)
(1)Donde los factores adicionales que influyen en el análisis son [10]:
Ko = factor de sobrecarga para resistencia flexionante
Ks = factor de tamaño
Km = factor de distribución de carga
KB = factor de espesor de orilla
Kv = factor dinámico
Para el cálculo y estimación de estos factores, existen métodos y fórmulas en la misma norma, a excepción del factor de sobrecarga Ko , en el que sólo se especifica que se debe considerar la probabilidad de variaciones que puedan causar cargas máximas mayores que Wt durante el funcionamiento. Sin embargo, no presenta valores específicos. Por tal motivo, diversos autores han establecido valores que juzgan adecuados con base en su experiencia para una aplicación particular [11], siendo una de las más reconocidas la propuesta de Shigley y Mischke [12], la cual se muestra en la Tabla 1.
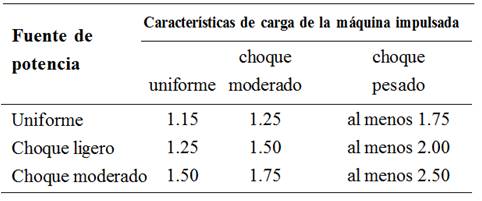
En la Tabla 1 se observa como característica principal que el valor de Ko para el nivel uniforme entre la fuente y la máquina impulsada es mayor que 1.0 ya que Shigley y Mischke [12] establecen que el factor de aplicación debe ser mayor, salvo que exista una clara evidencia que indique que la carga es perfectamente uniforme, situación que no se presenta comúnmente, ya que toda maquinaria tiene pares de torsión o fuerzas variando con el tiempo que influyen en el esfuerzo que experimentan los dientes en adición a los valores promedio [6].
Dada la ausencia de información definitiva sobre cargas dinámicas en máquinas impulsoras, en el presente trabajo se consideró sólo a la fuente de potencia uniforme empleando un motor eléctrico a velocidad constante [10] y aplicando el factor Ko en los tres niveles de carga para la máquina impulsada, la cual consideraría para analizar el incremento del esfuerzo sobre el diente con base en el grado de impacto de la maquinaria conectada al tren de engranes [6].
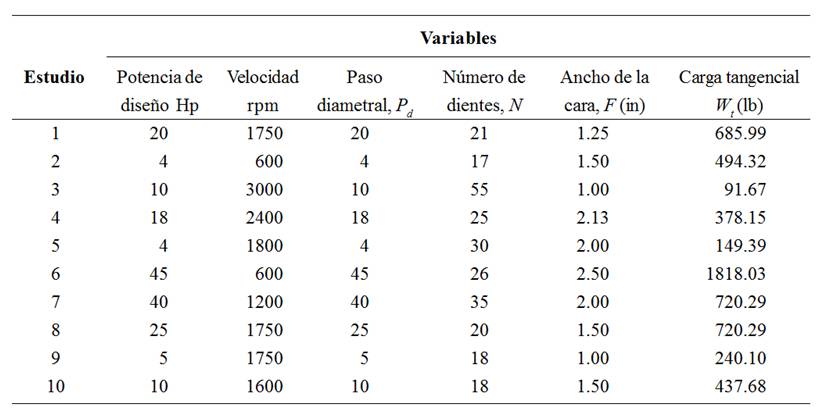
Para aplicar la ecuación de esfuerzo flexionante, en la Tabla 2 se presentan los datos de las variables principales para los diez casos de estudio analizados y sometidos a los tres niveles de carga mostrados en la Tabla 1, con una fuente de potencia uniforme.
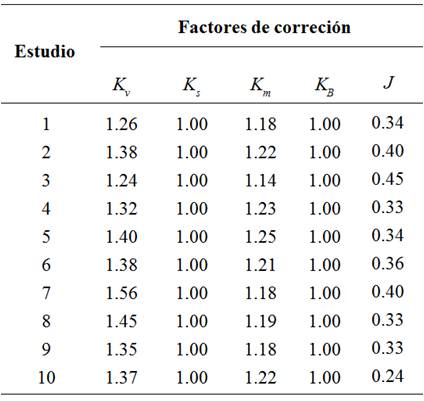
Finalmente, en la Tabla 3 se presentan los valores considerados para los factores de corrección con base en los criterios establecidos por la norma AGMA 2001-D04.
2.2. Análisis aplicando Ingeniería Asistida por Computadora
Hoy en día, los programas computacionales han logrado una mejora significativa en diversas áreas de la Ingeniería Mecánica generando un auge por las técnicas de computación y por el empleo de nuevos procesadores matemáticos cada vez más veloces que posibilitan el incluir nuevas técnicas de Diseño Asistido por Computadora (CAD) para el diseño y análisis de sistemas mecánicos, específicamente, en sistemas de engranaje [1], lo que ha hecho más común el uso de la Ingeniería Asistida por Computadora como una nueva referencia de análisis para la toma de decisiones, en conjunto con los estudios teóricos [13].
Para tal fin, existen diversos programas de CAE que se fundamentan en el Método del Elemento Finito, planteando ecuaciones que permiten una descripción cuantitativa del fenómeno estudiado. Este método es una herramienta que permite realizar una gran cantidad de análisis que difícilmente se obtienen por métodos analíticos clásicos [14]. De esta forma, el conocimiento del comportamiento mecánico en modelos ensayados virtualmente, permite diseñar productos más competitivos, de mejor calidad, en menor tiempo y a menor coste [15] con resultados confiables y acorde con la teoría [16].
Así, para esta segunda etapa de análisis, el programa seleccionado SolidWorks 2014 con su complemento SolidWorks Simulation y Catia V5R19 con su módulo Generative Part Structural Analysis, ambos por su alta capacidad de análisis y muy buena resolución numérica.
Para el desarrollo, se consideró la metodología de análisis propuesta por Carro et al., [8], en la cual, se aplican las restricciones en el soporte para el eje del engrane y se aplica la carga total en la cara superior del diente tal como lo propone Lewis [4], obteniendo como resultado final el esfuerzo de von Mises equivalente al teórico en el punto crítico.
En SolidWorks, la carga total se insertó en el estudio a través de sus componentes tangencial y radial, tal como se muestra en la Fig. 1 para facilitar la captura de los valores en el caso 1.
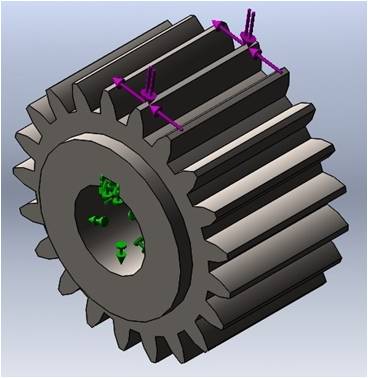
FIG. 1.
Análisis CAE con SolidWorks.
De la misma forma, en la Fig. 2 se muestra la configuración de la carga total y las restricciones sobre el modelo del caso 1 para el análisis CAE aplicando Catia.
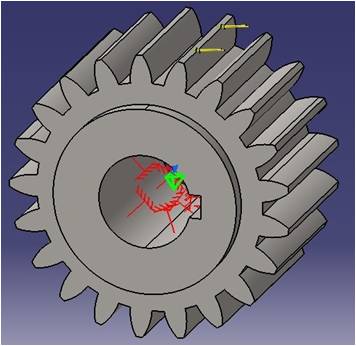
FIG. 2.
Análisis CAE con Catia.
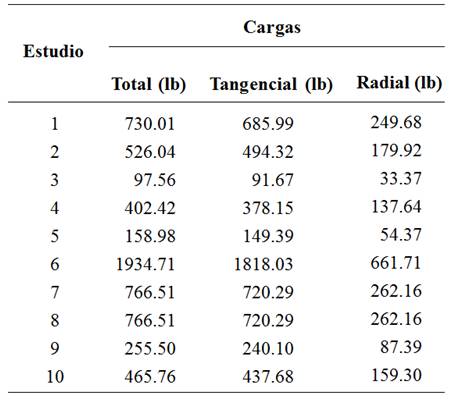
Una de las etapas más importantes en la realización de la simulación numérica es la definición del mallado tridimensional del modelo [15]. El software utilizado tienen la ventaja de estimar de forma automática el tamaño grueso, medio y fino de la malla en función de las dimensiones y de la forma geométrica de la pieza. Es claro que este parámetro influye en la precisión de los resultados y en la velocidad de cálculo [14], [15] por lo que para el presente trabajo se consideró el análisis con malla media y fina. Finalmente, las cargas requeridas para el análisis CAE de los diez casos propuestos se muestran en la Tabla 4.
En todos los casos, el punto crítico se ubicó en la vecindad de la raíz del diente, tal como se muestra en la Fig. 3 y la Fig. 4 que corresponden al caso 1, identificado con SolidWorks y Catia respectivamente.
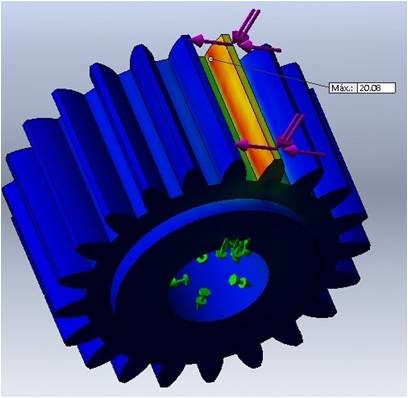
FIG. 3.
Punto crítico con SolidWorks.
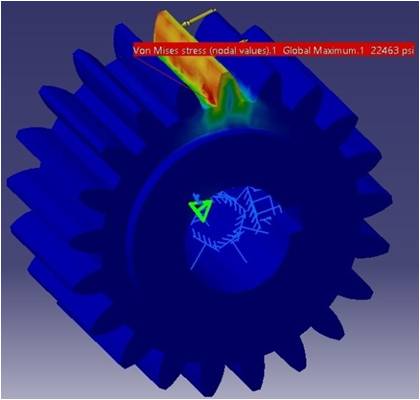
FIG. 4.
Punto crítico con Catia.
2.3. Análisis inferencial
El análisis inferencial se utiliza principalmente, para estimar parámetros poblacionales en las que la inferencia de dichos parámetros dependen de que se haya elegido una muestra probabilística que asegure un nivel de significancia, el cual, es un nivel que establece la probabilidad de equivocarse [17].
Existen dos niveles convenidos estadísticamente: p <0.01, que implica que en el análisis se tiene un 99% a favor y 1% en contra para generalizar sin temor, y p <0.05 que establece un 95% de seguridad y sólo un 5% en contra.
Con base en lo anterior y para determinar si existen diferencias significativas entre los resultados obtenidos por ambos métodos, en el presente trabajo se aplicó un análisis de varianza (ANOVA) para un modelo completo de bloques aleatorizados [18], que es una prueba estadística que analiza si más de dos grupos difieren significativamente entre sí en cuanto a sus medias.
Como resultado, produce un valor conocido como distribución F que es una razón que compara las variaciones entre y dentro de los grupos. Si el valor de F es significativo, implica que los grupos de interés difieren entre sí en sus promedios [17].
Finalmente, para identificar los componentes significativos que difieren, se aplicó la prueba de Tukey que es una prueba que realiza todas las posibles comparaciones de resultados de dos en dos, agrupando aquellos que presentan diferencias con un determinado nivel de significancia, que en este caso, fue del 95% ( p <0.05) [19]. Los resultados fueron obtenidos y analizados empleando Minitab 16.
3. Resultados
Los resultados obtenidos por el análisis teórico y por CAE de los diez casos considerados se muestran en la Tabla 5.
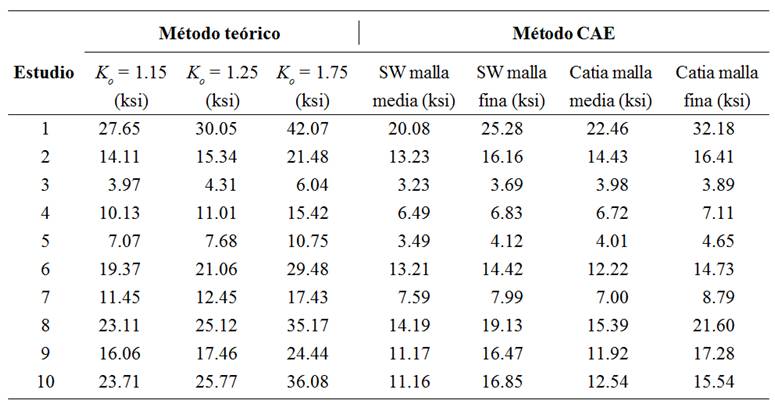
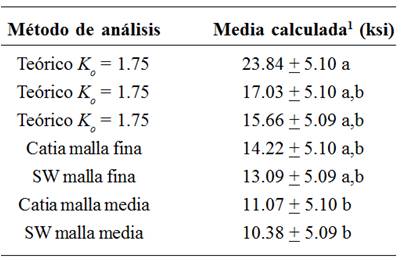
Asimismo, los resultados del análisis ANOVA con los datos de la Tabla 5, así como los de la prueba de Tukey correspondiente se muestran en las tablas 6 y 7 respectivamente.

4. Discusión de resultados
De los datos más relevantes de la Tabla 6, se observa que el cuadrado medio entre los resultados de los métodos de análisis es 206.04 que es varias veces mayor que el cuadrado medio del error (65.06), lo que indica que no es posible que las medias obtenidas sean iguales [18]. Para complementar esta afirmación, también se verifica que sí existen diferencias significativas ya que p <0.05 (0.009) lo que demuestra que al menos una media de los métodos de análisis es diferente.
Con base en lo anterior, en la Tabla 7 se muestra el resultado de la prueba de Tukey, la cual, indica que la media obtenida por el análisis teórico aplicando un factor de sobrecarga Ko = 1.75 representado por la letra a presenta una diferencia significativa ( p <0.05) en sus resultados. Asimismo, los resultados obtenidos por el análisis CAE en ambos software al aplicar una malla media también presentan una diferencia significativa ( p <0.05), siendo identificados por la letra b .
Los métodos aplicados con factor de sobrecarga uniforme y de choque moderado, así como los que aplicaron CAE con malla fina no presentaron diferencias significativas entre ellos, lo cual demuestra congruencia en sus resultados al realizar un estudio comparativo inferencial y también, que pueden ser considerados como una buena referencia y alternativa para la toma de decisiones.
Finalmente, de acuerdo con los resultados de este trabajo, se propone que el factor de sobrecarga sea contemplado como un factor de corrección que influya también en el esfuerzo resultante en CAE al aplicar un mallado medio o fino, siempre y cuando el criterio de diseño considere que Ko debe ser mayor a 1.25 por las características del sistema. De esta forma, se garantiza que no existan diferencias significativas que generen incertidumbre en los cálculos y en el análisis, ya que de acuerdo con la prueba de Tukey, no hay diferencias significativas entre la teoría con Ko< 1.25 y el análisis con mallado medio y fino.
5. Conclusiones
Como resultado de esta investigación se concluye que el análisis inferencial permitió cumplir con el objetivo de identificar si existen diferencias significativas al realizar un análisis de esfuerzo flexionante en engranes rectos aplicando métodos teóricos e Ingeniería Asistida por Computadora, resaltando el hecho de que el factor de sobrecarga y el mallado de la pieza son muy influyentes en los resultados.
Asimismo, se demuestra que el análisis teórico en conjunto con el análisis CAE son dos buenas alternativas para obtener resultados confiables y congruentes.
Por otra parte, se revela la importancia que tiene el incluir al factor de sobrecarga en el análisis teórico ya que influye significativamente en los resultados, por lo que se resalta el valor que tiene el determinarlo y seleccionarlo correctamente. Sin embargo, aún se depende del criterio del diseñador y sobre todo, de cómo visualiza el comportamiento del sistema.
De la misma forma, en el análisis CAE se observó que el mallado de la pieza puede influir significativamente, ya que puede llevar a obtener valores más precisos. No obstante, también depende de la precisión del modelado de la pieza en CAD, por lo que se recomienda que el análisis CAE siempre se realice con un mallado fino.
Referencias
[1] G. González, P. Frechilla and R. J. García, "El método de elementos finitos como alternativa en el cálculo de engranajes, " Revista Ingeniería Mecánica, no. 1, pp. 55-67, 2002.
[2] A. Fuentes and I. González, "Análisis tensional por elementos finitos de engranajes rectos con geometría modificada," Revista Iberoamericana de Ingeniería Mecánica, vol. 8, no. 1, pp. 15-30, 2004.
[3] T. M. Reydezel, G. Urriolagoitia G. and T. T. David, "Aplicación y análisis comparativo de los criterios de diseño mecánico por resistencia a esfuerzos, rigidez y modos de vibración," Científica, vol.11, no. 1,pp. 33-40, enero, 2007.
[4] A. C. Ugural, Mechanical Design An Integrated Approach, New York: McGraw Hill, 2004.
[5] G. Urriolagoitia, L. Hernández, G. Villa, Y. Medina. and H. Vázquez, "Aplicación de elementos finitos al diseño de engranes y algunos aspectos fundamentales relativos a la mecánica de fractura," Científica, no.4, pp. 1-7, julio, 1997.
[6] R. L. Norton, Diseño de máquinas, 4ª ed., México: Pearson Prentice Hall, 2013.
[7] J. Carro-Suárez, I. Flores-Nava and F. Flores-Salazar, "Análisis de esfuerzo de contacto en engranes rectos aplicando el criterio de Hertz con Ingeniería Asistida por Computadora," Científica, vol. 16, no. 1, pp. 25-32, enero, 2012.
[8] J. Carro-Suárez, I. Flores-Nava and F. Flores-Salazar, "Propuesta de una metodología para el análisis de engranes rectos aplicando Ingeniería Asistida por Computadora," presentado en el 10° Congreso Nacional de Mecatrónica, México, 2011.
[9] American Gear Manufacturers Association (AGMA), Norma 2001-D-04: Fundamental Rating Factors and Calculations Methods for Involute Spurs an Helical Gear Teeth, Virginia USA, 2004.
[10] R. L. Mott, Diseño de elementos de máquinas, 4ª ed., México: Pearson Prentice Hall, 2006.
[11] R. Budynas and J. K. Nisbett, Diseño en Ingeniería Mecánica de Shigley, 8ª ed., México: McGraw-Hill, 2008.
[12] J. E. Shigley and C. R. Mischke, Standard Handbook of Machine Design, 2a ed., New York: McGraw-Hill,1996.
[13] J. Carro-Suárez, I. Flores-Nava and F. Flores-Salazar, "La Ingeniería Asistida por Computadora como una alternativa de análisis de engranes helicoidales," presentado en First International Conference on Advanced Mechatronics, Design and Manufacturing Technology, AMDM 2012, Pereira, Colombia, 7-9 septiembre, 2012.
[14] J. A. Vázquez, Análisis y diseño de piezas de máquinas con Catia V5. México: Alfaomega, 2009.
[15] S. Gómez, SolidWorks Simulation, México: Alfaomega Ra-Ma, 2010.
[16] R. D. Chacón-Morón, M. J. Vergara-Paredes, M. A. Díaz-Rodrguez, and L. Andueza, "Programa de Simulación para Engranajes de dientes rectos por elementos finitos", Revista Ciencia e Ingeniería, vol. 32, no. 3, pp. 123-128, agosto, 2011.
[17] R. Hernández, C. Fernández and P. Baptista, Fundamentos de metodología de la investigación, México: McGraw-Hill, 2010.
[18] D. C. Montgomery, Diseño y análisis de experimentos, 2a ed., México: Limusa Wiley, 2014.
[19] E. Wong-González, "¿Después de un análisis de varianza... qué?," Agronomía Mesoamericana, vol. 21, no. 2, pp. 349-356, 2010.