Ciencia recreativa

Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivar 4.0 Internacional.
Recepción: 02 Noviembre 2016
Aprobación: 03 Abril 2017
Resumen: En este artículo estudiamos cuantitativamente las características básicas del efecto Doppler usando un péndulo cuyo bulbo está constituido por dos teléfonos inteligentes (smartphones). Uno de los teléfonos se usa para la medición de la velocidad angular y la emisión de una señal sonora de una frecuencia fija (monocromática) y el otro teléfono se emplea para grabar la señal de audio desde un sistema solidario al emisor. Un micrófono fijo, en el lugar más bajo de la trayectoria del péndulo y conectado a un ordenador o PC, graba la señal sonora desde un sistema de referencia fijo al laboratorio. De este modo podemos comparar las señales de audio, medidas por dos observadores, uno en reposo y el otro en movimiento respecto de la fuente, simultáneamente. Se desarrolla un modelo teórico sencillo que permite explicar los datos observados. El experimento es de muy bajo costo, conceptualmente simple y permite mostrar algunos aspectos de la relatividad de medición en un laboratorio de enseñanza o en el hogar.
Palabras clave: Efecto Doppler, Teléfono inteligente, Movimiento relativo, Relatividad.
Abstract: This article quantitatively studies the basic characteristics of the Doppler Effect by using a pendulum and two smartphones. The two smartphones act as the bulb of the pendulum. One of them measures the angular velocity and acts as a source for a sound signal of a fixed frequency (monochromatic signal). The second smartphone is used to record the audio signals in the source reference's frame. A microphone, connected to a personal computer, records the sound signal from a system of reference fixed to the laboratory. Thus we can compare audio signals measured by two observers, one at rest and the other one moving with respect to the source, simultaneously. It is possible to develop a simple theoretical model to explain the observed data quantitatively. The experiment is of low cost and conceptually simple. It allows us to explore some basic aspects of the theory of relative measurement in a teaching laboratory for beginners or at home.
Keywords: Doppler effect, Smartphone, Relative motion, Relativity.
Introducción
Seguramente todos hemos escuchado el sonido de la sirena de un vehículo que pasa por la calle, en especial, el cambio del tono de la sirena justamente al momento de pasarnos. Este conspicuo cambio de tono es muy evidente para el observador que está en la vereda, pero no para los pasajeros del vehículo. Si hubiésemos viajado en un coche a la misma velocidad que el vehículo con la sirena tampoco hubiéramos notado este cambio. Así, nos encontramos frente a un fenómeno en el que dos observadores que se mueven a una velocidad constante uno del otro, es decir dos observadores inerciales, perciben efectos físicos muy diferentes. Dado que la teoría de la relatividad especial describe cómo se relacionan las observaciones realizadas por dos observadores inerciales, este fenómeno acústico permite discutir a partir de situaciones al alcance de todos algunas implicaciones de esta importante teoría física (Drake y Purvis 2014).
En este trabajo la fuente emisora se encuentra en el bulbo de un péndulo y no constituye un sistema inercial, ya que está sometido a aceleraciones. Los detalles del movimiento del vehículo y el péndulo no son iguales, pues el primero se mueve con velocidad constante y el péndulo no. La analogía reside en que en ambos casos la fuente sonora pasa repentinamente de acercarse al observador a alejarse de él. Por lo que el tono del sonido cambia repentinamente de agudo a grave como consecuencia del efecto Doppler. La esencia del efecto que deseamos estudiar es la variación de la frecuencia percibida por un observador estacionario frente a la percibida por otro observador que se mueve con la fuente. Esta diferencia de percepción de un mismo fenómeno, en este caso la frecuencia de un tono, por dos observadores con velocidades diferentes, es lo que tiene en común el problema de efecto Doppler analizado aquí y la teoría de la relatividad. Buscamos con esta actividad contribuir a un aprendizaje significativo y duradero de este tipo de fenómenos (Carr 2009).
Cuando una fuente de sonido en movimiento se nos acerca, percibimos una mayor frecuencia que la emitida, es decir, al tono lo escuchamos más agudo. En cambio, al alejarse la fuente, el tono escuchado es más grave (Gil 2014, Young et al. 2009). El objetivo de este trabajo es estudiar cuantitativamente los cambios de frecuencia aparente de la fuente, cuando ésta se mueve respecto del observador.
Una manera simple de comprender este efecto se puede lograr con la siguiente analogía (Chakarvarti 1981, Gibbs 2013). Suponga que trabaja en una fábrica envasando chocolates que vienen hacia usted por una cinta transportadora que se mueve a velocidad constante  (figura 1). En un extremo de la cinta, un repositor pone los chocolates sobre la cinta (fuente de chocolates) a un ritmo constante,
(figura 1). En un extremo de la cinta, un repositor pone los chocolates sobre la cinta (fuente de chocolates) a un ritmo constante,  . Los chocolates por lo tanto, llegarán a usted (receptor) al mismo ritmo
. Los chocolates por lo tanto, llegarán a usted (receptor) al mismo ritmo  en que los depositó la otra persona (fuente). Ahora imagine que usted se acerca a la fuente con velocidad
en que los depositó la otra persona (fuente). Ahora imagine que usted se acerca a la fuente con velocidad  paralela a la cinta. Es claro que recogerá más chocolates por unidad de tiempo que en el caso anterior y su tasa de recolección
paralela a la cinta. Es claro que recogerá más chocolates por unidad de tiempo que en el caso anterior y su tasa de recolección  aumentará conforme sea mayor la relación
aumentará conforme sea mayor la relación  . Por otra parte, si el repositor de chocolates (fuente) se mueve hacia usted con velocidad
. Por otra parte, si el repositor de chocolates (fuente) se mueve hacia usted con velocidad  los chocolates sobre la cinta estarán más cerca uno de otro y usted los recibirá a una tasa mayor, según sea la relación
los chocolates sobre la cinta estarán más cerca uno de otro y usted los recibirá a una tasa mayor, según sea la relación  . Similarmente, si la persona que coloca los chocolates se mueve alejándose de usted, el espaciado de los chocolates en la cinta aumentará y la tasa de recepción
. Similarmente, si la persona que coloca los chocolates se mueve alejándose de usted, el espaciado de los chocolates en la cinta aumentará y la tasa de recepción  disminuirá. Esta analogía sirve para ilustrar la variación en una tasa o frecuencia de un proceso cuando el emisor o receptor se mueven respecto del otro y en relación al medio de transmisión (cinta transportadora en este caso).
disminuirá. Esta analogía sirve para ilustrar la variación en una tasa o frecuencia de un proceso cuando el emisor o receptor se mueven respecto del otro y en relación al medio de transmisión (cinta transportadora en este caso).
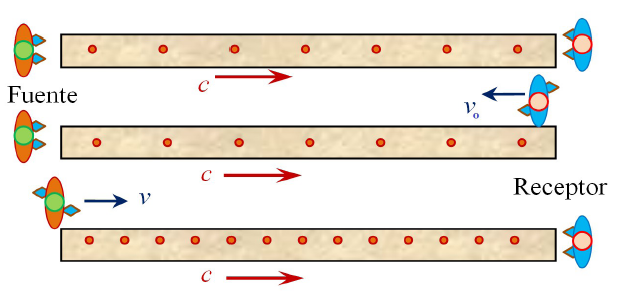
Figura 1.
Tres situaciones de un repositor (fuente) y un receptor de chocolates sobre una cita transportadora. (Arriba) Fuente y receptor en reposo. (Centro) Receptor acercándose a la fuente. (Abajo) Fuente acercándose al receptor.
Para el caso de fenómenos ondulatorios, este efecto es conocido
como efecto Doppler. Cuando una fuente emisora está en movimiento respecto a un
observador estacionario la frecuencia  detectada por éste viene dada
por:
detectada por éste viene dada
por:
 (1)
(1) donde  es la frecuencia emitida por la fuente,
es la frecuencia emitida por la fuente,  es la velocidad del sonido respecto del aire y
es la velocidad del sonido respecto del aire y  es la velocidad de la fuente respeto del medio. El signo negativo se usa cuando la fuente se acerca al observador y el signo positivo cuando se aleja (Resnick et al. 2001). Si no hay movimiento relativo entre el observador y la fuente, ambos miden la misma frecuencia. Cuando la fuente emisora acelera respecto al observador estacionario, la frecuencia
es la velocidad de la fuente respeto del medio. El signo negativo se usa cuando la fuente se acerca al observador y el signo positivo cuando se aleja (Resnick et al. 2001). Si no hay movimiento relativo entre el observador y la fuente, ambos miden la misma frecuencia. Cuando la fuente emisora acelera respecto al observador estacionario, la frecuencia  depende de cómo varíe
depende de cómo varíe  en el tiempo. Si esta función es conocida, la frecuencia instantánea percibida por el observador en un tiempo dado puede obtenerse evaluando la ecuación (1) a partir de la velocidad en ese instante.
en el tiempo. Si esta función es conocida, la frecuencia instantánea percibida por el observador en un tiempo dado puede obtenerse evaluando la ecuación (1) a partir de la velocidad en ese instante.
Aquí nos proponemos comparar las frecuencias experimentales medidas por ambos observadores (móvil y fijo) con los valores predichos por un modelo matemático, incorporando el teléfono inteligente como accesorio: instrumento de medición, generador de un tono puro y grabador de sonido. Algunos trabajos que buscan objetivos similares a los nuestros han incluido otros dispositivos de medición para su estudio y otras técnicas (Saba y Rosa 2003, Fernandes et al. 2016, Di Laccio et al. 2017).
Frecuencia Doppler en el experimento
La fuente emisora es parte del bulbo de un péndulo físico que se pone a oscilar con un ángulo para el cual no es posible realizar la aproximación de pequeñas oscilaciones. Medir la velocidad de la fuente respecto del sistema laboratorio es un problema a priori complicado, que hemos resuelto utilizando un teléfono inteligente. Éste mide la velocidad angular, que luego es utilizada para calcular la velocidad tangencial del bulbo. Este teléfono unido a otro similar conforman el bulbo de un péndulo de longitud  , que oscila en un plano vertical (figura 2). La función del segundo teléfono es grabar el sonido en un marco referencial solidario al primero, tiene velocidad nula respecto de la fuente pero no respecto al sistema laboratorio.
, que oscila en un plano vertical (figura 2). La función del segundo teléfono es grabar el sonido en un marco referencial solidario al primero, tiene velocidad nula respecto de la fuente pero no respecto al sistema laboratorio.
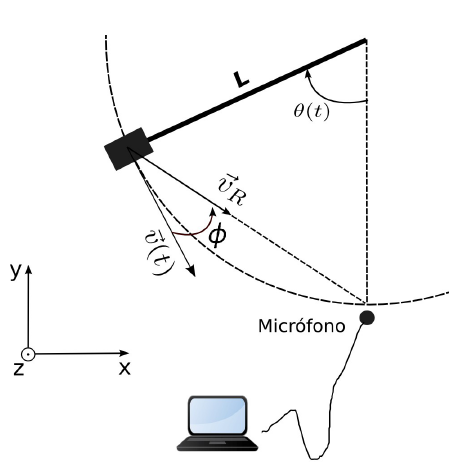
Figura 2.
Esquema del péndulo, las velocidades relevantes y el ángulo de oscilación.
El péndulo oscila en un plano, siendo acelerado por el campo gravitatorio. La velocidad angular varía en módulo a lo largo de su oscilación, lo que hace que la velocidad de la fuente, relativo al micrófono, sea una función del tiempo.
La velocidad tangencial del bulbo se obtiene con la ecuación (2):
 (2)
(2) donde  es la longitud del péndulo y
es la longitud del péndulo y  es la velocidad angular.
es la velocidad angular.
De la ecuación (2) podemos inferir que cuánto más largo sea el péndulo mayor será la velocidad tangencial del bulbo. Un bulbo que viaja más rápido permite cambios de frecuencias más notorios respecto de la fuente emisora, lo que facilita un mejor estudio del fenómeno. Por ejemplo, cuando la velocidad de la fuente es tan sólo el 1 % de la velocidad del sonido (es decir, cuando  0,01) el cambio es del 1 % de la frecuencia emitida y, si la velocidad de la fuente es el 10 % de la velocidad del sonido (
0,01) el cambio es del 1 % de la frecuencia emitida y, si la velocidad de la fuente es el 10 % de la velocidad del sonido (  0,1), el cambio será del 10 % de la frecuencia original. Si la frecuencia de la fuente fuese 5000 Hz, en el primer caso deberíamos esperar un cambio de 50 Hz y de 500 Hz en el segundo. El primer caso requiere de un análisis con mayor resolución en frecuencia para detectar las variaciones. La resolución con que es posible medir la variación de la frecuencia instantánea (resolución en frecuencia,
0,1), el cambio será del 10 % de la frecuencia original. Si la frecuencia de la fuente fuese 5000 Hz, en el primer caso deberíamos esperar un cambio de 50 Hz y de 500 Hz en el segundo. El primer caso requiere de un análisis con mayor resolución en frecuencia para detectar las variaciones. La resolución con que es posible medir la variación de la frecuencia instantánea (resolución en frecuencia,  ) es inversa a la resolución en el tiempo,
) es inversa a la resolución en el tiempo,  , (Aoki et al. 2009).
, (Aoki et al. 2009).
La velocidad relativa,  , es la componente de la velocidad tangencial en la dirección del observador. Si observamos la figura 3, esta componente es:
, es la componente de la velocidad tangencial en la dirección del observador. Si observamos la figura 3, esta componente es:
 (3)
(3)Para
determinar el ángulo  se realizó el análisis geométrico que aparece en la figura
3. De aquí se extraen las siguientes relaciones entre los ángulos:
se realizó el análisis geométrico que aparece en la figura
3. De aquí se extraen las siguientes relaciones entre los ángulos:
 (4)
(4)
 (5)
(5)
 (6)
(6)
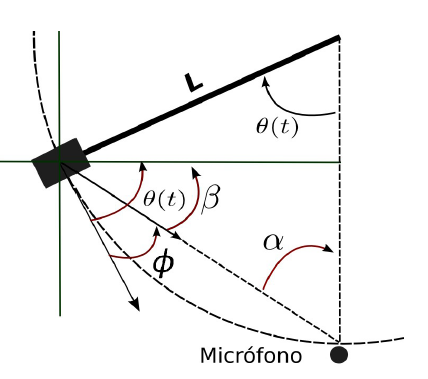
Figura 3.
Esquema que permite identificar las relaciones entre los ángulos de la situación y a partir de
ellas obtener el ángulo  en función de
en función de  , este se puede generar con
, este se puede generar con  y las
condiciones iniciales.
y las
condiciones iniciales.
A partir de las ecuaciones (4), (5) y (6) podemos concluir que:
 (7)
(7)Luego, combinando las ecuaciones (2) y (3) con el ángulo dado por la ecuación (7), la velocidad relativa al micrófono es:
 (8)
(8) La velocidad angular se mide directamente con el sensor giroscopio de un teléfono inteligente, colocado de forma tal que la oscilación sea entorno al eje  . Los ejes de giro solidarios a este son (
. Los ejes de giro solidarios a este son (  ,
,  ,
,  ). Viendo de frente la pantalla, el eje
). Viendo de frente la pantalla, el eje  es saliente y los ejes
es saliente y los ejes  e
e  son a lo ancho (sentido positivo hacia la derecha) y largo (sentido positivo hacia la parte superior del equipo). Los ejes cumplen con la regla del tornillo o tirabuzón de rosca derecha. El giro del teléfono a lo largo de cualquiera de los ejes anteriores proporciona datos de las componentes de velocidad angular. Cuando se produce un giro antihorario alrededor del eje en cuestión, el signo de la velocidad angular es positivo, mientras que es negativo para el caso horario (Gil y Di Laccio 2017). El período de recolección de datos del teléfono puede alcanzar los 5 ms, pudiendo el usuario seleccionar el período de muestreo de acuerdo a su experimento.
son a lo ancho (sentido positivo hacia la derecha) y largo (sentido positivo hacia la parte superior del equipo). Los ejes cumplen con la regla del tornillo o tirabuzón de rosca derecha. El giro del teléfono a lo largo de cualquiera de los ejes anteriores proporciona datos de las componentes de velocidad angular. Cuando se produce un giro antihorario alrededor del eje en cuestión, el signo de la velocidad angular es positivo, mientras que es negativo para el caso horario (Gil y Di Laccio 2017). El período de recolección de datos del teléfono puede alcanzar los 5 ms, pudiendo el usuario seleccionar el período de muestreo de acuerdo a su experimento.
El ángulo  se obtiene indirectamente empleando integración numérica para las condiciones iniciales del sistema,
se obtiene indirectamente empleando integración numérica para las condiciones iniciales del sistema,  y
y  .
.
A modo de ilustración se presenta aquí el algoritmo usado para generar el ángulo como función del tiempo:
 (9)
(9)La
ecuación (9) nos brinda el ángulo luego del primer período de medición a tiempo  . Para el siguiente período el ángulo viene dado por la ecuación
(10) y se corresponde con un tiempo
. Para el siguiente período el ángulo viene dado por la ecuación
(10) y se corresponde con un tiempo 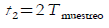
 (10)
(10)Este procedimiento se sigue iterativamente, de forma que lo podemos expresar como:
 (11)
(11) El subíndice  varía del primero al enésimo dato recolectado de la velocidad angular. Esta operación es sencilla de implementar en una hoja de cálculo. Conocida la longitud del péndulo, su velocidad angular y el ángulo
varía del primero al enésimo dato recolectado de la velocidad angular. Esta operación es sencilla de implementar en una hoja de cálculo. Conocida la longitud del péndulo, su velocidad angular y el ángulo  , se puede usar la ecuación (8) para obtener la velocidad relativa.
, se puede usar la ecuación (8) para obtener la velocidad relativa.
El uso del teléfono inteligente aporta una medida directa de la velocidad angular que simplifica notablemente el experimento, haciendo que no sea necesario resolver la ecuación de movimiento del sistema. Entendemos que esta forma de obtener la velocidad relativa es adecuada para alumnos de secundaria y estudiantes universitarios de primer año.
La velocidad del sonido en el aire  varía con la temperatura. Usando el modelo de gas ideal para un proceso adiabático se encuentra que
varía con la temperatura. Usando el modelo de gas ideal para un proceso adiabático se encuentra que  , donde
, donde  es el coeficiente adiabático del gas, R es la constate universal de los gases, T es la temperatura absoluta y M es la masa molecular del gas. Una aproximación útil de esta relación para aire seco y temperaturas cercanas a la temperatura ambiente es:
es el coeficiente adiabático del gas, R es la constate universal de los gases, T es la temperatura absoluta y M es la masa molecular del gas. Una aproximación útil de esta relación para aire seco y temperaturas cercanas a la temperatura ambiente es:  , donde
, donde  =331,4 m/s,
=331,4 m/s,  =0,61 m/s ºC y
=0,61 m/s ºC y  es la temperatura del medio medida en grados Celsius (Young et al. 2009).
es la temperatura del medio medida en grados Celsius (Young et al. 2009).
Respecto al sistema laboratorio la velocidad del observador es nula y la velocidad relativa viene dada por la ecuación (8). Usando lo anterior, la frecuencia Doppler para el péndulo es:
 (12)
(12)donde  debe calcularse a la temperatura al momento de realizar el
experimento.
debe calcularse a la temperatura al momento de realizar el
experimento.
Equipo y método
Para este experimento se utiliza un péndulo construido con una varilla delgada de aluminio de 1,75±0,02m, medida desde el eje de sujeción y hasta el altavoz del teléfono. El ángulo inicial que utilizamos es de ~60º respecto a la vertical y produce una rapidez máxima del bulbo de ~1 % de la velocidad del sonido. Para aumentar esta velocidad, puede aumentarse la longitud de la varilla o el ángulo desde donde se lo libera. El extremo de la varilla tiene un pequeño soporte que permite adherir dos smartphones. Uno de ellos genera un tono de frecuencia fija de 5000±1Hz, usando la aplicación Frequency Sound Generator y en forma simultáneamente registra la velocidad angular en función del tiempo con un período de muestreo de 10 ms. El segundo teléfono, solidario al anterior, graba el sonido emitido por el primero.

Figura 4.
Esquema simplificado del dispositivo experimental. Se sujetan en el extremo inferior los teléfonos inteligentes y luego se deja oscilar el sistema.
Un micrófono conectado a un ordenador personal o PC, graba el sonido emitido por el primer smartphone, desde un sistema de referencia en reposo respecto del laboratorio. El ordenador utiliza el programa Audacity (2017), que es de libre distribución, para el registro de la señal de audio, con una frecuencia de muestreo de 44100 Hz que supera más de 8 veces la frecuencia mínima que establece el Teorema de muestreo de Nyquist-Shannon (Horowitz y Hill 2015). Los datos obtenidos de las grabaciones se analizan con el programa Spectrogram16 (Auger et al. 1996, W5big 2004), que permite entre otras cosas: realizar un análisis tiempo-frecuencia, que es un análisis de Fourier sobre la señal cuyo contenido de frecuencia cambia en el tiempo. También se puede seleccionar la resolución en frecuencia (5 Hz en este caso), definir intervalos de tiempo de interés de la señal, colocar filtros, guardar en formato de imagen el espectro frecuencia-tiempo de la señal, etc.. De la imagen se pueden extraer los datos experimentales  usando el programa XY-Extract (Pereira da Silva y Pereira da Silva 2011).
usando el programa XY-Extract (Pereira da Silva y Pereira da Silva 2011).
Hay diferentes maneras de procesar estos datos, con mayor y menor grado de sofisticación. Existen programas de libre distribución que permiten un análisis detallado de las señales de audio o versiones más simples que permiten la extracción de los datos necesarios desde coordenadas en las imágenes. Dependiendo del contexto de enseñanza, el docente acordará con sus alumnos cuales son los más adecuados para sus fines.
El método propuesto aquí es el siguiente:
1. Se monta el dispositivo experimental de la figura 4, siendo conveniente que el péndulo tenga el mayor largo posible y se lo haga oscilar con una amplitud angular inicial grande (mayor de 45º), de modo de lograr la mayor velocidad relativa durante el pasaje por delante del micrófono del ordenador, y aumentar la variación de frecuencia del sonido respecto a la fuente. Los efectos de pandeo perpendicular al plano de oscilación pueden minimizarse con la rigidez de la barra y el poco roce del cojinete del eje del péndulo.
2. Se configuran los teléfonos para que uno realice la emisión de un tono puro (frecuencia elegida) y al mismo tiempo mida la velocidad angular del péndulo, y el otro grabe el sonido. Se configura el micrófono fijo al laboratorio para grabar la señal de audio con el ordenador.
3. Se inician las mediciones de forma sincronizada y se libera el péndulo para que comience a oscilar, dejando que realice varias oscilaciones antes de detener la recolección.
4. Se procesan los datos del experimento: se representa gráficamente  y de aquí se obtiene
y de aquí se obtiene  usando una hoja de cálculo. Las señales medidas se procesan para obtener, para cada señal, su espectro, es decir la
usando una hoja de cálculo. Las señales medidas se procesan para obtener, para cada señal, su espectro, es decir la  . En la obtención de
. En la obtención de  hay que prestar atención al correcto uso del signo de la ecuación (12) dado que el signo de la velocidad angular en general no acompaña el acercamiento/alejamiento.
hay que prestar atención al correcto uso del signo de la ecuación (12) dado que el signo de la velocidad angular en general no acompaña el acercamiento/alejamiento.
5. Finalmente se comparan los valores medidos de  , con las predicciones teóricas, obtenidas por la ecuación (12), utilizando la velocidad del sonido,
, con las predicciones teóricas, obtenidas por la ecuación (12), utilizando la velocidad del sonido,  , a la temperatura T del laboratorio. En nuestro caso, T=292 K (equivalente a 19 ºC).
, a la temperatura T del laboratorio. En nuestro caso, T=292 K (equivalente a 19 ºC).
Resultados
En la figura 5 se presenta un gráfico de la velocidad angular y el ángulo como función del tiempo. La velocidad angular se obtuvo directamente de los datos y el ángulo se obtiene mediante el procedimiento explicado en las ecuaciones (9) a (11), implementado en una hoja de cálculo.
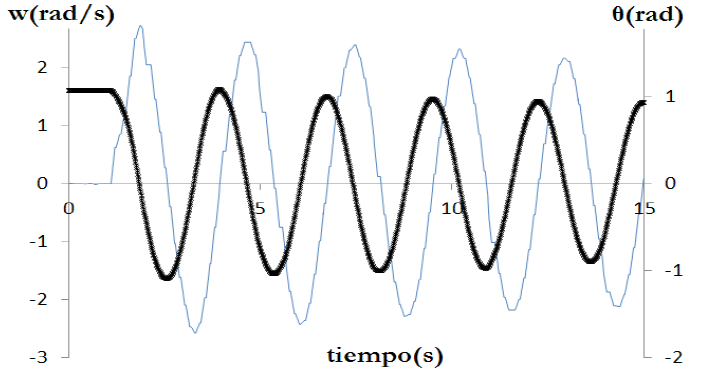
Figura 5.
Con trazo continuo fino se representa la velocidad angular y con un trazo más grueso el ángulo de oscilación respecto de la vertical. Las crestas y valles de la velocidad angular están asociadas a las máximas velocidades de acercamiento y alejamiento del teléfono al micrófono.
Se observa en el gráfico que el ángulo inicial es de aproximadamente 1,1 rad≈63º y la velocidad angular máxima es de 2,6 rad/s, disminuyendo levemente en cada oscilación debido al rozamiento con el aire y en el eje del péndulo. La disminución en la velocidad angular no afecta nuestro objetivo de medir la velocidad relativa y el teléfono. Resolver analíticamente la ecuación de movimiento del péndulo para grandes oscilaciones e introduciendo los efectos de rozamiento es posible pero superaría los prerrequisitos matemáticos de los alumnos, y por eso encontramos una alternativa confiable en el teléfono inteligente para determinar  y
y  . En la figura 6 se muestra una porción del espectrograma obtenido de la señal de audio del micrófono solidario al laboratorio. La imagen se obtuvo con el programa Spectrogram a partir de un archivo .wav (Wikipedia 2016). Los puntos pequeños son indicativos del proceso de extracción de datos con el editor de imágenes usado.
. En la figura 6 se muestra una porción del espectrograma obtenido de la señal de audio del micrófono solidario al laboratorio. La imagen se obtuvo con el programa Spectrogram a partir de un archivo .wav (Wikipedia 2016). Los puntos pequeños son indicativos del proceso de extracción de datos con el editor de imágenes usado.
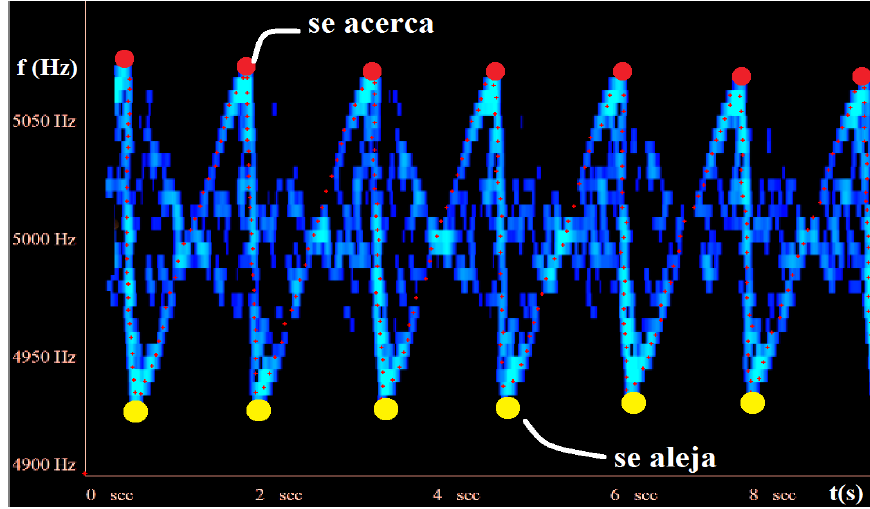
Figura 6.
Fragmento del espectrograma de la señal obtenido mediante Spectrogram16 con el micrófono. Los puntitos rojos indican los valores de frecuencia y tiempo que fueron seleccionados para cotejar con el modelo teórico. Los círculos rojos (frecuencias máximas) y los amarillos (frecuencias mínimas) resaltan respectivamente el acercamiento y el alejamiento del bulbo al micrófono.
La variación en la intensidad del trazo del espectrograma en los extremos de la trayectoria y en el lugar de equilibrio estable, se debe a que el número de frecuencia similares detectadas son en mayor cuantía que cuando realiza el resto del recorrido. Son fácilmente identificables los cambios de frecuencias al cambiar el péndulo de velocidad relativa en el trayecto de oscilación.
En la figura 7 se presentan en un mismo gráfico los cambios de frecuencias teóricos y experimentales (  del modelo teórico y
del modelo teórico y  de los resultados experimentales) en función del tiempo. Los valores experimentales de la frecuencia fueron obtenidos a partir de las imágenes generadas con Spectrogram y extraídos con el analizador de imágenes XY-Extract.
de los resultados experimentales) en función del tiempo. Los valores experimentales de la frecuencia fueron obtenidos a partir de las imágenes generadas con Spectrogram y extraídos con el analizador de imágenes XY-Extract.
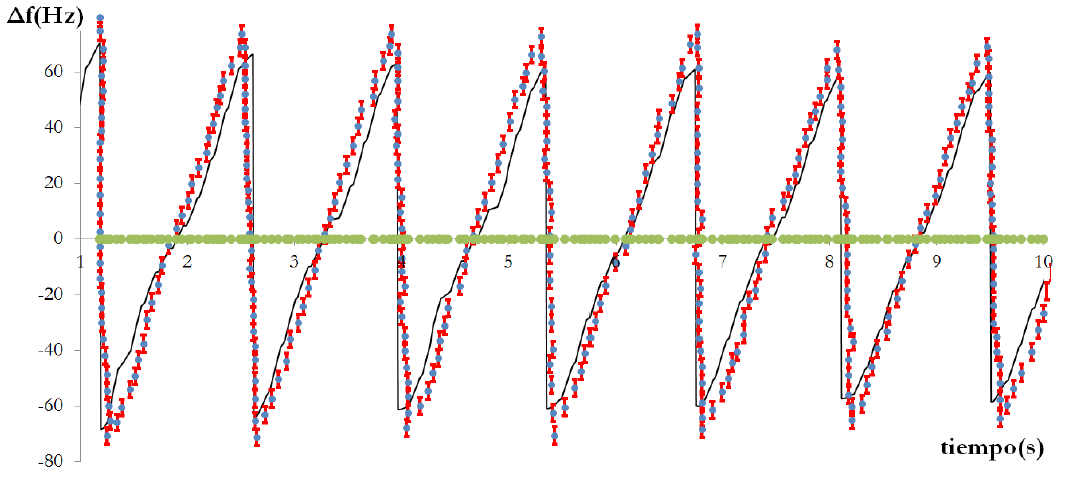
Figura 7.
Los cambios de frecuencia obtenidos con el modelo teórico se presentan en trazo continuo (negro). Con los símbolos discretos se presentan los cambios de frecuencias experimentales que fueron obtenidos con la técnica de análisis de espectrogramas. Los símbolos en el eje del tiempo indican que no hay variación de frecuencia observada por el teléfono solidario al otro.
Discusión
Para el observador solidario al primer teléfono no hay cambio apreciable de frecuencia y para el observador fijo al sistema del laboratorio se observan cambios del orden de 70 Hz por encima y debajo de la frecuencia del emisor. La inspección de la figura 7 muestra que el modelo teórico presenta una frecuencia menor a la experimental al ocurrir la transición de máxima velocidad a mínima. Esto se debe a la integración numérica, usada para obtener la función que describe el ángulo de oscilación,  , el cambio abrupto no permite tener suficientes datos recolectados para una mejor resolución. Una alternativa para lograr mayor precisión es ajustar la velocidad angular con un modelo teórico y luego integrar esta función.
, el cambio abrupto no permite tener suficientes datos recolectados para una mejor resolución. Una alternativa para lograr mayor precisión es ajustar la velocidad angular con un modelo teórico y luego integrar esta función.
Los resultados obtenidos permiten estudiar de forma adecuada el efecto Doppler. Un hecho sorprendente del análisis, que los mismos estudiantes descubren, es la notable diferencia entre lo que miden los dos observadores en diferentes referenciales; el solidario al laboratorio y el solidario al teléfono (fuente).
Para estudiantes que tengan menos preparación matemática es posible simplificar el experimento usando solamente los puntos de máxima velocidad de acercamiento y alejamiento. En ese caso se usa directamente la ecuación (1) y la comparación es directa con los puntos rojos y amarillos que se ilustra en el espectro de frecuencia de la figura 6.
Este experimento abre una ventana al estudio de un fenómeno de gran importancia en la Física a través de un experimento simple, y permite observar cómo se transforman las observaciones realizadas por dos observadores en dos sistemas de referencia, que es parte de la esencia de la teoría de la relatividad restringida. En este artículo no profundizaremos más en este importante punto, pero el lector interesado puede consultar otras fuentes pertinentes como (Drake y Purvis 2014, Bachman 1982). Por supuesto, el efecto Doppler descripto por la ecuación (1) resulta de aplicar la teoría clásica de la relatividad, es decir, las transformaciones de Galileo.
Otra extensión de este experimento, es que nos permite comprender por qué los espectros de luz emitidos por galaxias que se mueven a gran velocidad respecto a nosotros, presentan espectros desplazados hacia el rojo, tanto mayor cuanto mayor es su velocidad. Además, según describieron Hubble y Humason este corrimiento es tanto mayor cuanto mayor es su distancia a nosotros. Este importante descubrimiento nos conduce a comprender la teoría de la expansión de universo, que fundamenta la Teoría del Big Bang.
Conclusiones
El presente experimento ilustra un modo simple de realizar un estudio cuantitativo del efecto Doppler acústico, usando dos teléfonos inteligentes y un ordenador personal o PC con un micrófono. Los resultados se pueden ajustar muy bien usando un modelo simple del efecto Doppler. Se encontró un muy buen ajuste entre el modelo teórico y las frecuencias medidas por dos observadores inerciales.
Aquí tenemos un ejemplo simple de relatividad clásica. La diferencia entre las señales acústicas medidas por dos observadores inerciales es bien conspicua y clara, y permite introducir algunos conceptos básicos e importantes de la Física, como es la teoría clásica de la relatividad y comprender la importancia del descubrimiento de la expansión de universo.
Esta actividad demuestra que los teléfonos inteligentes son instrumentos adecuados y accesibles no sólo para realizar experiencias sencillas sino también para realizar experimentos más sofisticados. Estos teléfonos facilitan la determinación de la velocidad de acercamiento-alejamiento y son un recurso valioso para el aula laboratorio.
La propuesta incorpora diferentes técnicas transversales de trabajo experimental que pueden extrapolarse al estudio de otros fenómenos. Esto permite en los alumnos un aprendizaje que no se limita solamente a esta propuesta en concreto sino que ayuda a aprender a través de experiencias que le son amigables y creativas.
Referencias
Aoki K., Mitsui T.,Yamamoto Y. (2009) Direct quantitative measurements of Doppler effects for sound sources with gravitational acceleration. Inédito. Recuperado de: https://arxiv.org/pdf/0911.3819.pdf
Audacity (2017) Audacity. Recuperado de: www.audacityteam.org
Auger F., Flandrin P., Gonçalvès P., Lemoine O. (1996) Time-Frequency Toolbox, For Use with MATLAB. CNRS (Francia) - Rice University (USA). Recuperado de: http://tftb.nongnu.org/tutorial.pdf
Bachman R. A. (1982) Relativistic acoustic Doppler effect. American Journal of Physics 50, 816-818. Recuperado de: http://aapt.scitation.org/doi/abs/10.1119/1.12747
Carr J. J. (2009) Teaching Special Relativity. The Physics Teacher 47, 485. Recuperado de: http://aapt.scitation.org/doi/abs/10.1119/1.3246460
Chakarvarti S. K. (1981) The Doppler effect: A simple analogy and demonstration. The Physics Teacher 19, 320. Recuperado de: http://aapt.scitation.org/doi/abs/10.1119/1.2340792
Di Laccio J. L., Ferrón M., Gil S., Alonso-Suárez R. (2017). Efecto Doppler: ¿Cómo tenemos evidencia de su existencia? Revista Novedades Educativas 316, 64-70. Recuperado de: http://www.noveduc.com/l/revista-novedades-educativas-316-abril-2017/1799/03283534
Drake S. P., Purvis A. (2014) Everyday relativity and the Doppler effect. American Journal of Physics 82, 52-59. Recuperado de: http://aapt.scitation.org/doi/abs/10.1119/1.4830887?journalCode=ajp
Fernandes A. C. P., Auler L. T. S., Huguenin J. A. O., Balthazar W. F. (2016) Efeito Doppler com tablet e smartphone. Revista Brasileira de Ensino de Física 38 (3), e3504. Recuperado de: http://www.scielo.br/pdf/rbef/v38n3/1806-1117-rbef-38-03-e3504.pdf
Gibbs K. (2013) Schoolphysics. The Doppler Effect, Fig. 2. Recuperado de: http://www.schoolphysics.co.uk/age16-19/Wave%20properties/Doppler%20effect/text/Doppler_effect/index.html
Gil S. (2014) Experimentos de Física usando TIC y elementos de bajo costo. Buenos Aires. Alfaomega.
Gil S., Di Laccio J. L. (2017) Smartphone: una herramienta de laboratorio y aprendizaje: laboratorios de bajo costo para el aprendizaje de las ciencias. Latin American Journal of Physics Education 11, 1305. Recuperado de: http://www.lajpe.org/mar17/1305_Salvador_2017.pdf
Horowitz P., Hill W. (2015) The Art of Electronics, 3rd ed. Cambridge. Cambridge University Press.
Pereira da Silva W., Pereira da Silva C. (2011) xyExtract Graph Digitizer. Recuperado de: http://zeus.df.ufcg.edu.br/labfit/index_xyExtract.htm
Resnick R., Halliday D., Krane K. (2001) Física, Vol. 1, 4ª ed. México. Compañía Editorial Continental.
Saba M. F., da S. Rosa R. A. (2003) The Doppler Effect of a Sound Source Moving in a Circle. The Physics Teacher 41 (2), 89-91. Recuperado de: http://aapt.scitation.org/doi/10.1119/1.1542044
Young H., Freedman R., Sears F., Zemansky M. (2009) Física Universitaria, Vol. 1. México. Pearson Education.
W5big (2004) Spectrogram. Recuperado de: http://w5big.com/spectrogram.htm
Información adicional
Para citar este artículo: Di Laccio
J. L, Vitale G., Alonso-Suárez R., Pérez N., Gil S. (2017) Estudio del efecto
Doppler utilizando teléfonos inteligentes. Revista Eureka sobre Enseñanza y
Divulgación de las Ciencias 14 (3), 637-646. Recuperado de: http://hdl.handle.net/10498/19512
Enlace alternativo
http://revistas.uca.es/index.php/eureka/article/view/3588 (html)
