Prácticas de modelación matemática desde una perspectiva socio crítica con estudiantes de grado undécimo

Mathematical modeling practices from a critical perspective with high school students

Esta obra está bajo una Licencia Creative Commons Atribución 4.0 Internacional.

El trabajo que reportamos en este documento se desarrolló con un grupo de estudiantes de grado undécimo de educación media de un colegio público de Bogotá (Colombia), situado en una zona habitada por una comunidad de bajos recursos económicos. En este contexto, los estudiantes deben afrontar una serie de contradicciones de tipo social y cultural, procedentes de una desorganización política de la comunidad y una escuela que se preocupa únicamente por presentar un listado de contenidos como herramienta para afrontar las problemáticas de la vida.

Como consecuencia de lo anterior, los estudiantes se plantean un proyecto de vida individualizado e inmediatista, que deja de lado una posición crítica frente a los fenómenos que cotidianamente deben afrontar. Así, en general, su forma de afrontar su proyecto de vida no prioriza el contar o formar parte de organizaciones colectivas que propendan por cambios en la sociedad.

En cuanto a la institución educativa podemos señalar que cuenta con un grupo de profesores que intenta construir una propuesta educativa que integre las diferentes disciplinas, en aras de contraponerse a esa organización lineal por contenidos sugerida de manera implícita desde los organismos oficiales, planteando alternativas de aprendizaje más significativo.

En este sentido, las clases de matemáticas han propendido por la incorporación del uso de las nuevas tecnologías en un aula especializada, lo que ha posibilitado una dinámica de clase que da al profesor espacios para no ser un expositor de contenidos y el rol del estudiante no es el de simple observador. Lo anterior ha permitido avanzar en una propuesta de auto aprendizaje que asume un rol del profesor como mediador que acompaña el proceso de cada estudiante. Sin embargo, aún no se ha conseguido profundizar en un trabajo que potencie la construcción colectiva de conocimiento, al tiempo que relacione las problemáticas que aquejan cotidianamente a los estudiantes y sus comunidades.

Por las razones expuestas en los párrafos anteriores, nace la necesidad de plantear una propuesta, desde el aula de matemáticas, cuyo objetivo gire en torno a integrar las problemáticas cercanas a los estudiantes con el aprendizaje de conceptos matemáticos, al mismo tiempo que se reflexione sobre las implicaciones y responsabilidades sociales que surgen al comprender los soportes matemáticos de los fenómenos sociales.

Para dar cuenta de tal propuesta, presentaremos a continuación a la modelación matemática como fuente de lineamientos para construir ambientes de clase, en donde se analicen fenómenos sociales y los conocimientos matemáticos surjan de este análisis, gracias a las discusiones entre los participantes. Posteriormente plantearemos algunas conceptualizaciones metodológicas desde un paradigma crítico de la investigación, lo que nos permitirá analizar, a manera de ejemplo, algunos apartes del ambiente de modelación matemática creado. Al final daremos algunas conclusiones al respecto.

En los documentos y disposiciones oficiales emanados en Colombia, –particularmente documentos como los Lineamientos Curriculares presentados por el Ministerio de Educación Nacional (MEN) (1998) –se reconoce y se resalta, como un proceso general importante en la clase de matemáticas, la modelación matemática. Al respecto se señala:

Cuando hablamos de la actividad matemática en la escuela destacamos que el alumno aprende matemáticas “haciendo matemáticas”, lo que supone como esencial la resolución de problemas de la vida diaria, lo que implica que desde el principio se integren al currículo una variedad de problemas relacionados con el contexto de los estudiantes.

La resolución de problemas en un amplio sentido se considera siempre en conexión con las aplicaciones y la modelación. La forma de describir ese juego o interrelación entre el mundo real y las matemáticas es la modelación. (MEN, 1998. p. 76).

De allí, podemos afirmar que se plantea que los estudiantes deben “vivir la actividad matemática”. Es decir, que deben dejar de lado aquellas actividades matemáticas en las clases centradas –por parte del estudiante– en escuchar, estar atento a lo que el profesor señala, imitar, entrenar, … y al final aplicar; por una en la que puedan proponer soluciones y confrontarlas con las de sus compañeros, puedan defenderlas y discutirlas.

A la luz de lo anterior, en el documento de los Lineamientos Curriculares se afirma que los modelos matemáticos –dependiendo del conocimiento, intereses e intenciones del que resuelve el problema– “[...] estructuran y crean un pedazo de realidad” (MEN, 1998. p. 77). Señalan además, que transferir una situación real en un problema planteado matemáticamente, implica el desarrollo de actividades como:

• Identificar las matemáticas específicas en un contexto general;

  esquematizar;

  formular y visualizar un problema en diferentes formas;

  descubrir relaciones;

  descubrir regularidades;

  reconocer aspectos isomorfos en diferentes problemas;

  transferir un problema de la vida real a un problema matemático;

  transferir un problema del mundo real a un modelo matemático conocido. (Treffers & Goffree, citados por MEN, 1998. p. 77).

Así mismo en este documento se afirma que una vez que se tiene un modelo matemático conocido, el problema puede ser atacado y tratado con herramientas matemáticas, lo que presupone el desarrollo de actividades como:

• representar una relación en una fórmula;

  probar o demostrar regularidades;

  refinar y ajustar modelos;

  utilizar diferentes modelos;

  combinar e integrar modelos;

  formular un concepto matemático nuevo;

  generalizar. (Treffers & Goffree, citados por MEN, 1998. p. 77).

De lo anterior podemos concluir que la Modelación Matemática ­–tal y como se señala en documentos oficiales en Colombia– puede ser vista y entendida como una competencia que se relaciona con un objetivo de aprendizaje. En este último sentido Rojas, Salazar & Romero (2013), Blomhoj (2009), Mancera, Camelo, Salazar & García (2014), entre otros, mencionan que en esta idea de la Modelación Matemática resulta determinante la integración de los modelos matemáticos y de la modelación matemática, como medios de aprendizaje de las matemáticas (y como una competencia importante en sí misma).

De lo anterior, puede deducirse que la modelación matemática, desde una mirada educativa, busca adaptar o recrear las etapas de la actividad científica en la escuela para la comprensión o construcción de un concepto matemático.

Sin embargo, autores como Barbosa (2006) plantean que en lugar de “medir” qué tanto se aproximan los estudiantes a la modelización como actividad científica, se consideren otras posibilidades cuyo énfasis residen en la reflexión sobre el papel de las matemáticas en la sociedad. Araújo (2009) enfatiza en la importancia de que los alumnos, además de trabajar en grupos al abordar problemas que les resulten socialmente relevantes, escogidos por ellos mismos, orienten el desarrollo del proyecto de modelación matemática bajo la luz de cuestiones levantadas por la educación matemática crítica.

Así, un proyecto de modelación matemática orientado por aspectos sociales, políticos y críticos, debe promover la participación crítica de los estudiantes/ciudadanos en la sociedad, al discutir asuntos políticos, económicos o ambientales en los que las matemáticas sirven como soporte tecnológico (Skovsmose, 1994).

Bajo este panorama, aceptamos, entonces, con Silva & Kato (2012) que las actividades de modelación matemática desde la perspectiva sócio crítica deben considerar, al menos, las siguientes cuatro categorías (con sus respectivas subcategorías):

• Abordar un problema socialmente relevante para los estudiantes: Trabajo en grupo, participación crítica y democrática en las clases y escogencia del problema por parte de los estudiantes.

  Participación activa del estudiante en la construcción del modelo: Desarrollo de acciones comunitarias, aplicación del modelo al contexto del estudiante e importancia de las matemáticas en la sociedad.

  Participación activa del estudiante en la sociedad: Uso de problemas socialmente relevantes, elección del problema por parte de los estudiantes, interpretación del modelo de acuerdo a la realidad y consideración de la cultura de los estudiantes.

  Actuación del docente como mediador: Trabajo en grupo, elección del problema por parte de los estudiantes, consideración la cultura de los estudiantes e importancia de las matemáticas en la sociedad.

Bajo estas consideraciones, en este trabajo damos cuenta de un ambiente de modelación matemática en la perspectiva sócio crítica, que hemos creado con estudiantes de grado undécimo de un colegio público de Bogotá (Colombia), con el objetivo de establecer posibilidades y desafíos para crearlos y desarrollarlos.

Para ello, partimos por aceptar con Araújo, Campos & Camelo (2015) que tales ambientes pueden ser entendidos como ambientes de aprendizaje donde los estudiantes son invitados a investigar, usando las matemáticas, situaciones traídas de sus contextos socialmente relevantes, a la vez que interpretan y reinterpretan el mundo que los rodea (Mancera et al., 2014). En este sentido, la intensión no es solamente la de desarrollar habilidades en la realización de cálculos y procedimientos matemáticos, sino también la de posibilitar espacios para que los estudiantes participen críticamente de la sociedad en que se desenvuelven, siendo las matemáticas un soporte tecnológico.

Para el desarrollo del trabajo que mencionamos en los apartes anteriores, comenzamos por aceptar que lo que sucede en la enseñanza y aprendizaje en las clases de matemáticas, está relacionado con lo que sucede en prácticas sociales dentro de una institución escolar (Gutiérrez, 2013 y Valero, 2012). Siendo necesario para comprender lo que allí acontece, realizar descripciones y análisis detallados de interacciones entre sujetos. Además, debíamos posibilitar que se reflexionara sobre el poder y las subjetividades, conectando lo que acontece en dichas prácticas sociales con las dinámicas externas a la escuela, por lo que los momentos históricos, la cultura, las dinámicas económicas y políticas en que se dan, debíamos considerarlas. Es decir, la opción metodológica para dar cuenta de este trabajo debía inscribirse en un paradigma crítico de la investigación educativa, que posibilitara incorporar aspectos sociopolíticos de la educación matemática (Vithal, 2000; Skovsmose & Borba, 2004 y Valero, 2012).

De acuerdo con Vithal (2000) este tipo de investigación en el aula de matemáticas debe posibilitar ir más allá de una interpretación, incluso compleja, de lo que acontece en el aula de matemáticas. Pues un asunto esencial bajo presupuestos sociales, culturales y políticos es el cambio, ya que no se trata únicamente de interpretar lo que está sucediendo, sino de revertir el statu quo en una dirección que la comunidad consensua según sus intereses particulares.

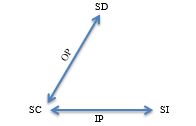
Dicho cambio, podemos entenderlo, interpretarlo y analizarlo al aceptar tres tipos de situaciones que Vithal (2000) llama: corriente (SC), imaginada (SI) y dispuesta (SD). La SC la conceptualizamos como aquella situación que de manera natural se presenta en los diferentes contextos de trabajo. La SI la representamos como una situación ideal que está pensada por los integrantes de la comunidad que están participando, ésta situación contiene las ideas hipotéticas, los conceptos y los ejemplos cercanos a la práctica que se selecciona y que será reinterpretada desde el campo teórico de acuerdo con la comprensión del contexto en el que tal práctica se llevará a una forma particular. Según Skovsmose & Borba (2004) existe una conexión entre las SC y SI denominada imaginación pedagógica (IP), pues es a través de esta que los participantes de la investigación imaginan una situación particular desde una SC. Agregan estos investigadores que en tal imaginación se debe identificar alternativas a la SC (Skovsmose, 2015). De esta manera se ofrecen posibilidades de cambio, debido a la existencia de alternativas que muestran que la SC no es "una necesidad". Aunque debe interpretarse de manera dinámica, en la figura 1 puede representarse dicha relación.

[1]
Componentes SC, IP y SI del Modelo de la investigación crítica (adaptado de Skovsmose & Borba 2004).
Autor

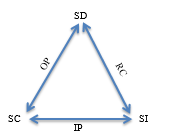
En cuanto a la SD, plantea Vithal (2000) que es una situación real, pero reorganizada, creada y constituida en consenso por los participantes de la investigación. Tal situación es desarrollada con referecia a las ideas planteadas y a la inspiración que pueda dar la SI. Debemos resaltar que la SD se desarrolló con referencia a la SI, creando oportunidades para que se analice cómo se desarrollan los acontecimientos en relación con el marco teórico existente. Por lo que el cambio es inherente a este tipo de trabajo. Skovsmose & Borba (2004) plantean, además, que podemos relacionar las SC con las SD a través de las organizaciones prácticas (OP) de las instituciones educativas (ver figura 2). Para explicar dicha organización, estos investigadores, afirman que el contexto educativo limita la IP, pues las exigencias políticas y las necesidades del contexto no permiten, entre otros aspectos, que lo imaginado sea idéntico a lo desarrollado.

[2]
Modelo parcial de la investigación crítica (adaptado de Skovsmose & Borba 2004).
Autor

Por último, encontramos que según Skovsmose & Borba (2004), la SD se relaciona con SI a través de un razonamiento crítico (RC), pues no se trata únicamente de dar cuenta de lo que aconteció en la SD y de cómo se desarrolló, sino de sacar conclusiones acerca de las ideas educativas que se habían expresado en la SI. Así, las conclusiones afectan no sólo a la SC que gracias al desarrollo de las SD ya ha sido cambiada o afectada, dando lugar a un tipo de investigación crítica, sino también a la SI, pues podemos estar investigando “lo que no es, pero que podría ser” (Skovsmose, 2015). En la figura 3 puede apreciarse una representación de las relaciones mencionadas, las cuales deben interpretarse, como ya mencionamos, de manera dinámica.

[3]
Modelo de la investigación crítica (Skovsmose and Borba 2004).
Autor

Para la construcción de los datos se hizo una descripción de la SC que persiguió, por una parte, reconocer y describir todos aquellos aspectos que puedan relacionarse con el ambiente de modelación matemática a ser analizado. De otra parte, y como pretendemos reconocer prácticas educativas institucionalizadas para las clases de matemáticas desde la voz de los diferentes actores (estudiantes y profesores), elaboramos registros de lo que acontece en la escuela a través de notas de campo, recogida de evidencia documental y entrevistas.

Luego de lo anterior, planteamos –el profesor y los estudiantes–, la posibilidad de desarrollar un ambiente de modelación matemática (SI y SD) que recogió tanto de la perspectiva sócio crítica de la modelación matemática, como de la metodología crítica de investigación desarrollada en el apartado anterior. A partir de allí, sistematizamos las producciones de los estudiantes a través de videos, audios y entrevistas semi estructuradas con la intención de evidenciar aspectos relacionados con las subcategorías propuestas al final del segundo apartado. En síntesis, procedimos de la siguiente manera:

1. 1. Hicimos una caracterización de la institución en general y del grupo de estudiantes en particular a partir de las percepciones sociales y culturales que el profesor y los estudiantes manifestaron, por lo que nos permitirnos conocer y construir un acercamiento al conocimiento del territorio en el que están los estudiantes.
2. 2. Construimos junto con los estudiantes y el profesor un ambiente de modelación en la perspectiva crítica.
3. 3. Grabamos en audio y video todas las sesiones y discusiones en clase.
4. 4. Valoramos el material sistematizado en relación con las categorías propuestas por Silva & Kato (2012).

Con base en los presupuestos anteriores, creamos un ambiente que se desarrolló en cinco sesiones de clase, en el que analizamos aspectos del actual modelo de telefonía móvil en Colombia. La idea central del ambiente fue posibilitar evidencias en torno de las categorías propuestas, frente a aspectos que los estudiantes consideraran relevantes en el sistema de telefonía móvil colombiano, buscando con ello que las reflexiones que los estudiantes presentaran, involucraran –además de aspectos matemáticos– las implicaciones sociales de tales reflexiones y sus consecuencias. Para ello fue determinante la actuación del profesor como mediador, pues en la elección de la temática central del ambiente se tuvo en cuenta su conocimiento acerca de la cultura y del contexto de los estudiantes. Situación que resultó clave para el ambiente de clase, pues se posibilitó a los estudiantes determinar y escoger aspectos sobre los que querían trabajar. Además estimuló la discusión, con los grupos y entre los grupos, enfatizando en: las implicaciones sociales de los diferentes aspectos seleccionados, cómo con las matemáticas se podía identificar una comprensión crítica de cada uno de dichos aspectos, el papel de cada uno de ellos en la sociedad e identificar con las matemáticas otras formas de percibir el contexto en el que viven y conviven.

Por la extensión de este documento, solo mostraremos algunos análisis de la sesión dos, pues consideramos que lo que sucedió allí, posibilita ilustrar lo que se pretende en este documento.

Como el grupo de estudiantes no tenía experiencia en el desarrollo de ambientes de modelación matemática y el profesor tampoco había trabajado de manera explícita estas actividades, se decidió proponer un marco general en el que los estudiantes pudieran explorar posibilidades para desarrollar una investigación que les permitiera plantear y entender, basados en ideas matemáticas, alguna problemática sensible a sus percepciones. Lo precedente, considerando que Barbosa (2004) resalta que los ambientes de modelación matemática en la perspectiva socio crítica pueden comenzarse de tres maneras diferentes a saber: i) el profesor propone a los estudiantes sobre qué investigar, delimitando el problema claramente; ii) el profesor coloca un marco general en el que los estudiantes pueden decidir sobre qué investigar o iii) los estudiantes proponen sobre qué investigar.

En este sentido, en la primera sesión, se planteó observar un video[1] que muestra una versión de los factores que están involucrados en el costo de los teléfonos móviles en Colombia, problemática que consideramos podría interesar a los estudiantes por dos motivos: i) los y las jóvenes hacen uso de esta herramienta tecnológica para comunicarse a través del chat y la redes sociales y ii) recientemente se promulgó una ley que pretende reducir los costos tanto de los teléfonos móviles, como del servicio prestado por llamadas y datos.

Luego de observar el video, se solicitó a los estudiantes reflexionar y proponer en grupos de cuatro integrantes posibles problemáticas que desearan investigar, en relación con el modelo de telefonía móvil. Además, que dichas problemáticas deberían poderse explicar con el uso de matemáticas y de ser posible, ofrecer alternativas de solución, usando también, soportes matemáticos. De esta manera el grupo de estudiantes interactuó con la problemática a la luz de las subcategorías que esbozamos en el segundo apartado.

Durante la segunda sesión, cada grupo de estudiantes realizó una presentación que, de manera general, pretendía dar a conocer la problemática que estudiarían. Tanto los integrantes de los otros grupos, como el profesor, tendrían la función de aportar a la delimitación de la problemática planteando posibles caminos para abordarla y fuentes de información para la elaboración de un marco teórico. Las problemáticas presentadas fueron: dificultades en la conexión o “llamadas caídas”; tiempo que se invierte usando el celular y la reposición; robo de los celulares; duración de las baterías; daños en la salud causados por el uso del celular y costo de los teléfonos móviles en Colombia y en el exterior.

Llamó la atención que el primer grupo en realizar su presentación planteó una dramatización de la situación, en la cual se mostraba, a manera de sarcasmo y comedia, una dificultad en la conexión de las llamadas, pues no es habitual que los estudiantes presenten de esta manera, los problemas en la clase de matemáticas. Lo anterior nos permitió inferir que los estudiantes estaban aceptando la invitación de buscar problemáticas en sus cotidianidades y trayéndolas al espacio del aula para pensarlas, posibilitando puentes entre su realidad y las clases de matemáticas. Aquí, la medicación del profesor se hizo preponderante, pues discutió con el grupo para acotar y puntualizar una posible pregunta de investigación, veamos el siguiente diálogo extraído de las discusiones que se presentaron en clase. Hemos usado E y P para representar lo expresado por los estudiantes y el profesor respectivamente.

E1: Los problemas que queremos representar acá es que la señal es muy mala, en muchas ocasiones llamamos y se cae la señal. También el minuto nos lo cobran muy caro, hasta ahorita están experimentando lo del cobro por segundo, pero no en todos los casos están así. Entonces nos cobran el minuto muy caro, …

P: ¿cómo podríamos hacer para comenzar a solucionarlo?

E1: primero es que eso es más como problema de las empresas …, pues todavía les falta que implementen el cobro por segundo…

P: ¿dónde se les ocurriría a ustedes buscar para solucionarlo?

[los estudiantes se miran entre ellos e intercambian miradas, hay un silencio]

E2: para solucionarlo, mmm eh…!!! [silencio, risas]

Aquí puede observarse que, aunque los estudiantes han traído una dificultad de sus cotidianidades, no han profundizado en las causas del por qué la señal de la telefonía móvil no es la más adecuada, o por lo menos no es la que ellos esperan. Por lo que la actuación mediadora del profesor resulta preponderante toda vez que ve aquí una posibilidad para plantear que se estudien aspectos que se relacionen con los problemas que los estudiantes están señalando, consiguiendo que recreen sus realidades y, quizás, informadamente tomen posicionamientos críticos. Así, se le da importancia al trabajo en grupo, la elección del problema por parte de los estudiantes y se considera su cultura.

[luego del silencio de la transcripción anterior]

P: Recuerden que en un segundo momento ustedes deben buscar información para solucionar el problema. ¿qué buscarían ustedes?

E1: Podríamos hablar con…

E2: las empresas…

E2: investigar cada costo y cada plan que da cada empresa [...] ver cual roba más [risas]

P: O sea, que en principio es buscar los planes que ofrece cada empresa y …

E2: [cortando la palabra del profesor] si y comparándolos ...

En el anterior fragmento puede observarse que la mediación que realiza el profesor, permite evidenciar una concientización de las actuaciones y de la forma de pensar de los estudiantes en relación con el aspecto que están profundizando. Situación que le proporciona información precisa sobre el sentido que los estudiantes le dan a las informaciones encontradas, el sentido de dichas informaciones con las matemáticas y particularmente le da información de cómo, los estudiantes, van construyendo sus conocimientos.

En el siguiente fragmento la estudiante E2 continúa relatando una situación en la que le ofrecen un plan por un costo y luego le cobran por encima de ese costo, preguntándose por qué pasará eso, pues en su experiencia le ha sucedido varias veces.

E3: [un estudiante de los que observa la presentación] hay un problema de economía. Por ejemplo, en [un supermercado], uno compra una avena, y una avena esta valiendo $3970, a ti te cobran $4000.

[...]

¿Pelearías por esos [$30][2]?

E2: Pues no. Pero el caso aquí, es que nos cobran cosas que no estamos usando. Como el internet.

Observamos aquí, un intento de posicionamiento crítico, pues es necesario el redondeo para el pago o cobro de estas tarifas y no por ello puede afirmarse que las empresas nos están robando o haciendo un mal cobro. En un pasaje de la discusión más adelante, el profesor insiste.

P: Demos herramientas para que ellas [un grupo de estudiantes] investiguen donde pueden encontrar para solucionar el problema.

E3: Falsa publicidad.

P: [acentuando con su cabeza] investiguemos qué hay sobre falsa publicidad. Ahorita ellas van a entrar a internet y van a buscar, ¿dónde podría buscar? [...] ¿qué otra cosas podrían mirar ellas para investigar?

En la transcripción anterior el profesor continúa intentando mediar en la necesidad de aclarar una problemática interesante para que sea abordada por los estudiantes. La discusión continúa y se establecen posibles preguntas en torno a la calidad de la señal.

En otro segmento de la misma clase, uno de los estudiantes intenta plantear el por qué es importante entender el sistema de robos de celulares en Bogotá, llegando a la siguiente pregunta: “¿por qué es posible vender un celular robado si está reportado?” El profesor aprovecha la discusión para plantear una pregunta en torno de la importancia de las matemáticas en la sociedad.

P: Yo le devuelvo una pregunta que usted hacía ayer. ¿qué se le ocurre a usted que podamos usar de las matemáticas en eso? [...]

E: [algunos estudiantes en coro] la cantidad de robos de celulares, ¿cuánto pagan por liberar un celular?, estadísticas de robos…

En una conversación posterior con el investigador, el profesor argumenta que quedó con la sensación que los estudiantes ven matemáticas porque aparecen números, mostrándose escéptico frente a un posible uso de las matemáticas de manera cualitativa en este grupo de estudiantes. Lo anterior pone de manifiesto una forma en que el profesor reconocer a sus estudiantes como sujetos que aprenden, además de una preocupación sobre la importancia de las matemáticas que están desarrollando sus estudiantes alrededor del aspecto estudiado.

Es importante resaltar que al ser esta una de las primeras sesiones del ambiente de modelación, se ha posibilitado que los estudiantes planteen sus discusiones en torno de aspectos principalmente de tipo social, más que de tipo matemático; pues consideramos, con Valero (2012), que lo social siempre antecede a lo matemático si lo que interesa va más halla de la aprensión de habilidades y destrezas de tipo algorítmico a una preocupación por comprender el mundo con las matemáticas.

Durante la segunda parte de la sesión, los estudiantes discutieron sus presentaciones e intentaron plantear una posible pregunta para investigar aspectos de la telefonía móvil. Particularmente observamos allí que los estudiante trabajan de manera eficiente en los grupos y dado el momento y la temática que deseaban trabajar, predominaron intervenciones orales en las que relataban experiencias vividas. Así mismo, se evidencia que la información consultada en internet, hace repensar la pregunta a plantear y posibilita nuevas comprensiones del problema:

E2: Acá dice que. Muestra como una solución.

P: ¿ De qué?

E2: aquí [señalando la información que ha encontrado en internet] muestra una solución y muestra cómo sincronizar las antenas [para mejorar la señal] entonces nosotros podríamos. [...]

P: ¿Cuál es su tema?

E2: Nosotros tenemos la cobertura. Pero entonces, la pregunta que nosotros nos podríamos hacer, si ya están presentado una solución es: ¿por qué no ha funcionado?; ¿Qué es lo que falta para hacerlo?

En esta variación o acotación de la pregunta, podemos apreciar claramente que los estudiantes, se cuestionan ahora sobre el por qué no se ha implementado una solución que proviene de un trabajo realizado como tesis de maestría en una de las más reconocidas universidades colombianas, lo que les implica comenzar a tomar una distancia crítica del fenómeno a estudiar inicialmente ¿por qué se cae la señal? a uno más profundo, ¿por qué no han implementado una solución para que no se caiga la señal si ya hay estudios que muestran cómo diseñar el sistema de antenas para que esto no ocurra?

Durante la tercera sesión, los estudiantes presentaron un primer acercamiento a la comprensión de la problemática y una posible solución. Llamó la atención que todos los grupos presentaron algún tipo de acercamiento a la problemática y que desarrollaron presentaciones con el uso de aplicativos digitales, lo que evidenciaba que estaban aceptando la invitación a construir el ambiente de modelación matemática. Además se vislumbra como los estudiantes no solamente hacen un esfuerzo importante para escoger una problemática a desarrollar, sino que la van acotando –por una parte– gracias a la mediación tanto del profesor como de los otros grupos de estudiantes –y por otra– a la búsqueda de información y delimitación de los referentes conceptuales que van abordando para la solución de dicha problemática, situación que potencia la participación activa y democrática de los estudiantes en la construcción del modelo.

El desarrollo de ambientes de modelación matemática en el aula de clase, desde la perspectiva sócio crítica, promueve, tal y como señala Blomhoj (2009), Kaiser & Sriraman (2006), Barbosa (2009) y Araújo (2009), participaciones críticas de los estudiantes, gracias a las reflexiones sobre los modelos matemáticos que están construyendo, situación que permite empoderarlos como ciudadanos autónomos e independientes en la sociedad.

Como consecuencia, los ambientes de modelación, desde la perspectiva sócio crítica, pueden ser considerados como posibilidades para explorar los papeles que la matemática debería desempeñar en la sociedad, permitiéndonos pensar en una propuesta en educación matemática más política para los estudiantes, que les permita asumir posicionamientos críticos (como los mencionados por Araújo (2009), Barbosa (2004), Valero (2012) y Mancera, et al. (2014)) en nuestra sociedad. Lo anterior, se dio gracias a la participación activa de los estudiantes en la construcción del modelo matemático, pues además de discutir en pequeños grupos y presentar sus ideas de manera organizada, estuvieron dispuestos y receptivos frente a las sugerencias que sus compañeros y profesor les plantearon, reajustando las consideraciones que los conducían a comprender un fenómeno social y a presentar posibles soluciones a las problemáticas identificadas. Hecho que a su vez evidencia un pequeño e importante giro por parte de los estudiantes, y del profesor, sobre la perspectiva de aprendizaje asumida y sus implicaciones en relación con las actividades, las interacciones y la forma de conocer y posicionarse en el mundo con las matemáticas.

En cuanto a la actuación del docente, queremos resaltar que fue gracias a su rol que la SC fue transformándose a una SD que, considerando de manera simultanea tanto la OP como la IP, posibilitó al grupo de estudiantes repensar las problemáticas a estudiar y acotarlas de tal modo que no solo los contenidos matemáticos fueran importantes, sino que, y como lo señala Valero (2012), lo social siempre antecediera a lo matemático, proporcionando posibilidades para que aprendizajes significativos acontecieran en el ambiente construido. De esta manera, intereses centrados en la emancipación, orientaron el ambiente de modelación matemática desarrollado, ubicándonos, tal y como lo menciona Gutiérrez (2013), en una dimensión política de la Educación Matemática.

Un gran desafío, identificado al construir y desarrollar el ambiente, fue reflexionar sobre las implicaciones sociales que ellos debían asumir al comprender de una manera más crítica fenómenos de sus cotidianidades, pues una respuesta a preguntas como: ¿y ahora que comprendemos este fenómeno qué deberíamos hacer con esta información identificada? No fue resuelta satisfactoriamente. Por lo que es necesario en futuros trabajos centrar la atención en aspectos en torno de las proyecciones que podría derivarse del trabajo en estos ambientes de modelación.

Queremos resaltar que implementar metodologías en las que no se prescribe el aprendizaje es una experiencia enriquecedora, pues posibilita vivenciar alternativas de aprendizaje, en las que se explora, como plantea Skovsmose (2015, p. 72) “lo que no es pero pudiera ser”. En este sentido identificamos que es posible, desde los ambientes de aula de matemáticas, crear espacios en los que tanto estudiantes como profesor comprenden el contexto en el que se encuentran y se atreven a buscar alternativas para su transformación (lo que no es), aunque sea en el plano teórico (pudiera ser), como se evidenció en esta experiencia.